If S=3t3+9t2+2t+7 , then distance travelled by the particle during the first second of its motion is
7 units
21 units
14 units
28 units
The correct Answer is:C
Step by step video, text & image solution for If S =3t^(3)+9t^(2)+2t+7 , then distance travelled by the particle during the first second of its motion is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APLICATIONS OF DERIVATIVESBook:MARVEL PUBLICATIONChapter:APLICATIONS OF DERIVATIVESExercise:MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP - I : CHAPTER 12)
Explore 19 Videos
- APLICATIONS OF DERIVATIVESBook:MARVEL PUBLICATIONChapter:APLICATIONS OF DERIVATIVESExercise:MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP - II : CHAPTER 12)
Explore 19 Videos
- APPLICATIONS OF DEFINITE INTEGRALS Book:MARVEL PUBLICATIONChapter:APPLICATIONS OF DEFINITE INTEGRALS Exercise:TEST YOUR GRASP
Explore 11 Videos
Similar Questions
The position of a particle along x-axis at time t is given by x=1−t+t2. The distance travelled by the particle (in 'm') in first 2 seconds is 's'. Fill '2s' in OME sheet.
View SolutionA particle is moving along positive x direction and experiences a constant acceleration of 4m/s2 in negative x direction. At time t=3 second its velocity was observed to be 10m/s in positive x direction.
(a) Find the distance travelled by the particle in the interval t=0 to t=3s. Also find distance travelled in the interval t=0 to t=7.5s..
(b) Plot the displacement – time graph for the interval t=0 to 7.5s.
View Solution
Knowledge Check
If S=13t3−4t2+12t, then distance travelled by the particle before it first comes to rest is
A323 unitsB32 unitsC643 unitsD64 unitsThe position of a particle moving rectilinearly is given by x=t3−3t2−10. Find the distance travelled by the particle in the first 4 seconds starting from t=0.
A24 unitB36 unitC15 unitD50 unitIfS=2t3−4t2+12t, then distance travelled during the time -interval [0,1] is
A4 unitsB9 unitsC8 unitsD10 units
A particle is moving in a striaght line and at a given time, its displacement is S=t3−6t2+9t, where t is in seconds and S is in meter . The total distance travelled by the particle during the first five seconds is
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionThe position x of a particle varies with time t as x=6+12t−2t2 where x is in metre and t is in seconds. The distance travelled by the particle in first five seconds is
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
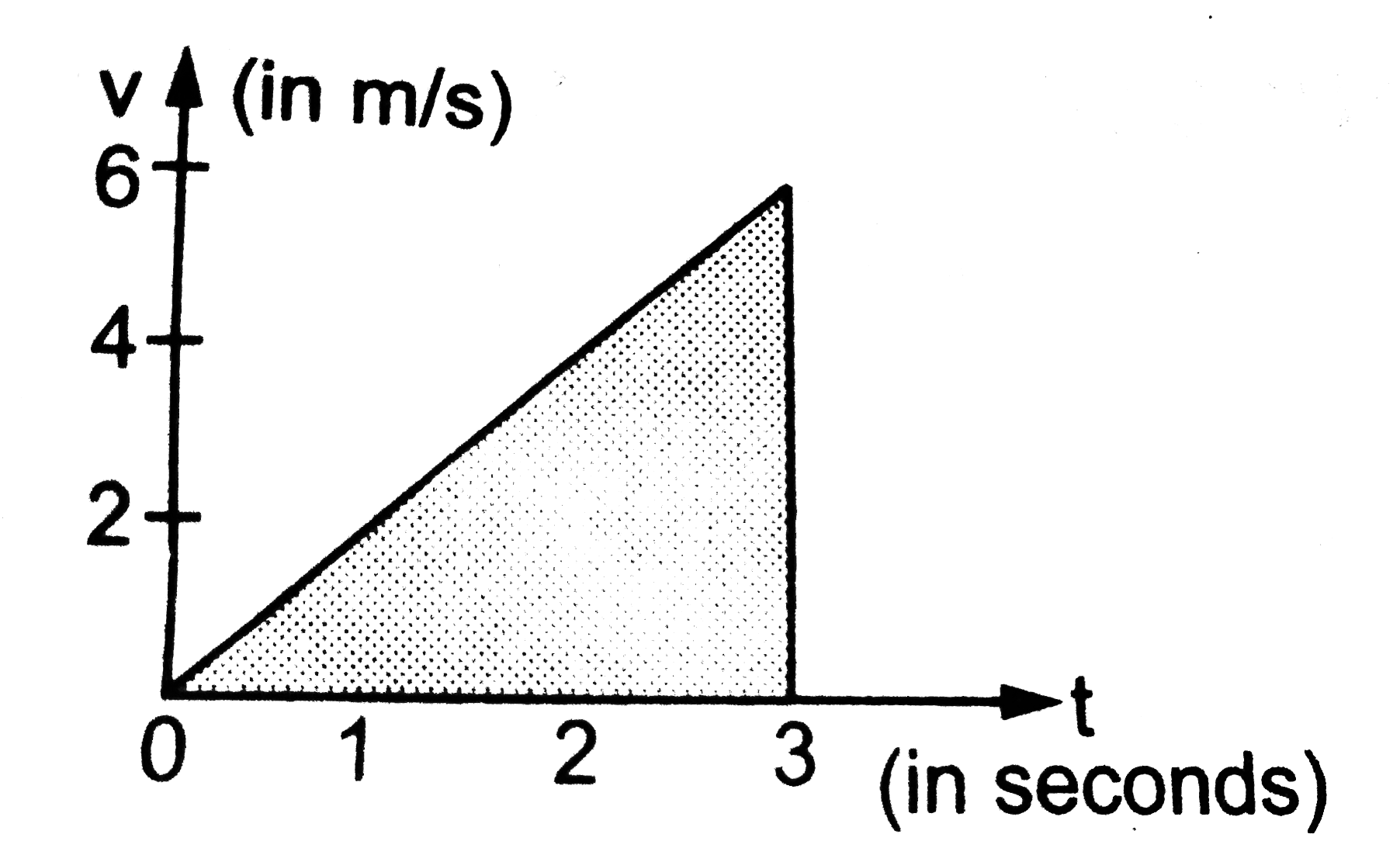
View SolutionIf the distance s travelled by a particle in time t is s=asint+bcos2t, then the acceleration at t=0 is
View Solution

