The potential energy (in SI units) of a particle of mass 2kg in a conservative field is U=6x−8y. If the initial velocity of the particle is →u=−1.5ˆi+2ˆj, then find the total distance travelled by the particle in the first two seconds.
The correct Answer is:15m
→F=−∂U∂xˆi−∂U∂yˆj=−6ˆi+8ˆj
→a=→F/m−3ˆi+4ˆj has same direction as that of
→u=−1.5ˆi+2ˆj
|→a|=5,|→v|=52
Since →u and →a are in same direction, particle will move along a straight line, so the distance covered
S=52×2+12×5×22=15m
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Single Correct
Explore 100 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.5
Explore 15 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
The potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionA particle is moving under a constant acceleration of 3m/s2. The initial velocity of the particle is 10m/s. calculate the distance travelled by the particle is 5s and also in th 5th second of its motion.
View Solution
Knowledge Check
The position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
A1 mB2 mC2.5 mD3 mIn the figure the variations of componets of acceleration of particles of mass 1kg is shown w.r.t. time. The initial velocity of the particle is →u=(−3ˆi+4ˆj)m/s. the total work done by the resultant force on the particles in time intervals from t=0 to t=4 seconds is :
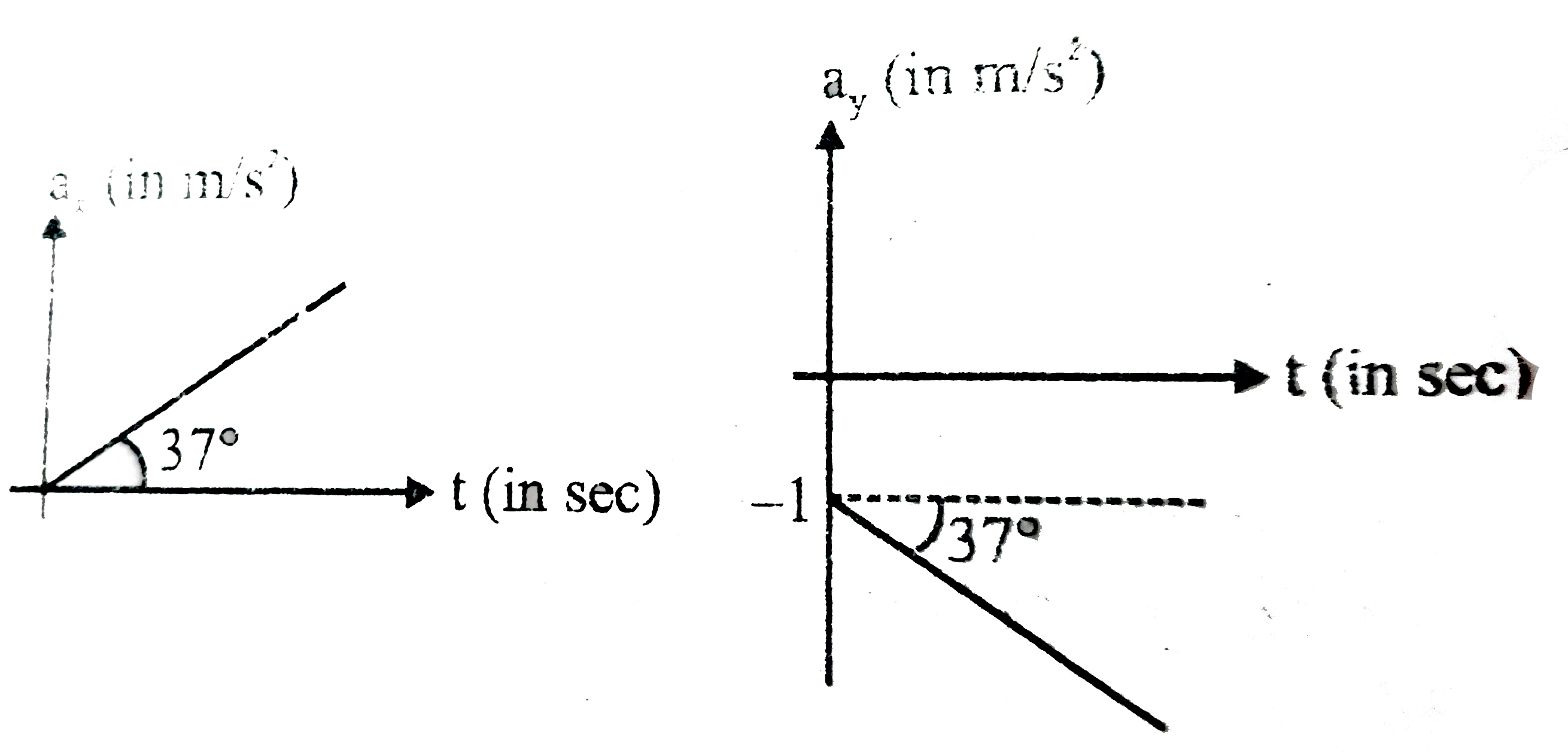 A22.5JB10 JC0DNone of these
A22.5JB10 JC0DNone of theseThe potential energy of a particle of mass 1 kg in a conservative field is given as U=(3x2y2+6x) J, where x and y are measured in meter. Initially particle is at (1,1) & at rest then:
AInitial acceleration of particle is 6√5ms2BWork done to slowly bring the particle to origin is 9 JCWork done to slowly bring the particle to origin is −9 JDIf particle is left free it moves in straight line
A particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
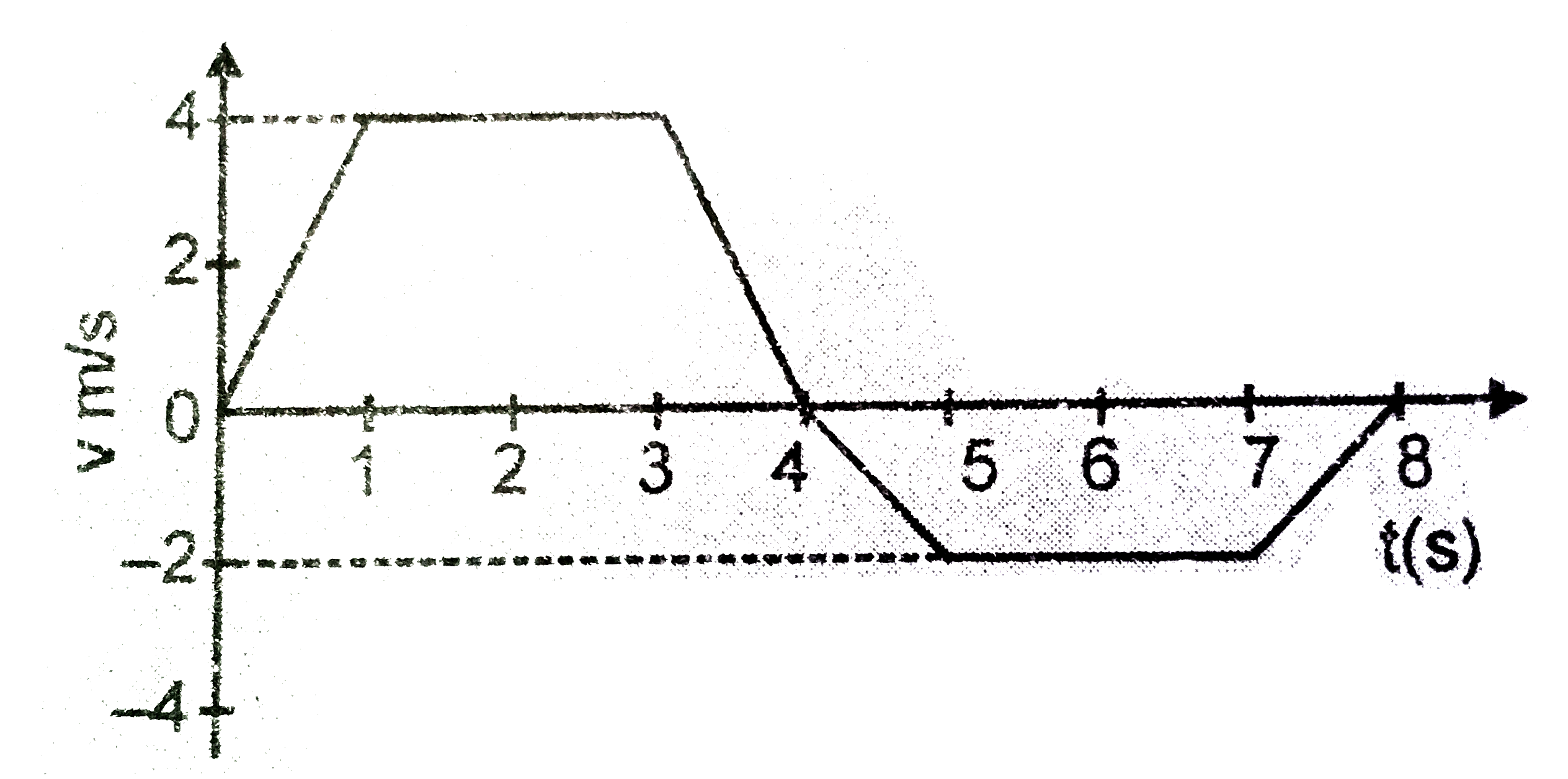
View SolutionThe potential energy of a particle of mass 1 kg free to move along x-axis is given by U(x)=(x22−x) joule. If total mechanical energy of the particle is 2J then find the maximum speed of the particle. (Assuming only conservative force acts on particle)
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionThe potential energy of a particle of mass 1 kg in a conservative field is given as U=(3x2y2+6x)J, where x and y are measured in meter. Initially particle is at (1, 1) & at rest, then incorrect statement is :
View SolutionThe potential energy in joules of a particle of mass 1 kg moving in a plane is given by U=3x+4y, the position coordinates of the point being x and y, measured in metres. If the particle is initially at rest at (6, 4), then:
View Solution

