A resistance R2 is connected in parallel with a resistance R1 what resistance R3 must be connected in series with the combination of R1andR2 so that the equivalent resistance is equal to the resistance R1 -
R21R1+R2
(R1+R2)2R1
R22R1+R2
R21R2
The correct Answer is:A
Accordingly R1R2R1+R2+R3=R1
Topper's Solved these Questions
Similar Questions
Knowledge Check
Resistance n, each of rohm, when connected in parallel give an equivalent resistance of Rohm. If these resistances were connected series, the combination would have a resistance in ohm, equal to
An2RBR/n2CR/nDnRR is the equivalent resistance of n resistors of same resistance in series. If the connection is turned parallel then equivalent resistance will be:
An2RBnRCRnDRn2If a resistanceR2 is connected in parallel with the resistance R in the circuit shown, then possible value of current through R and the possible value of R2 will be
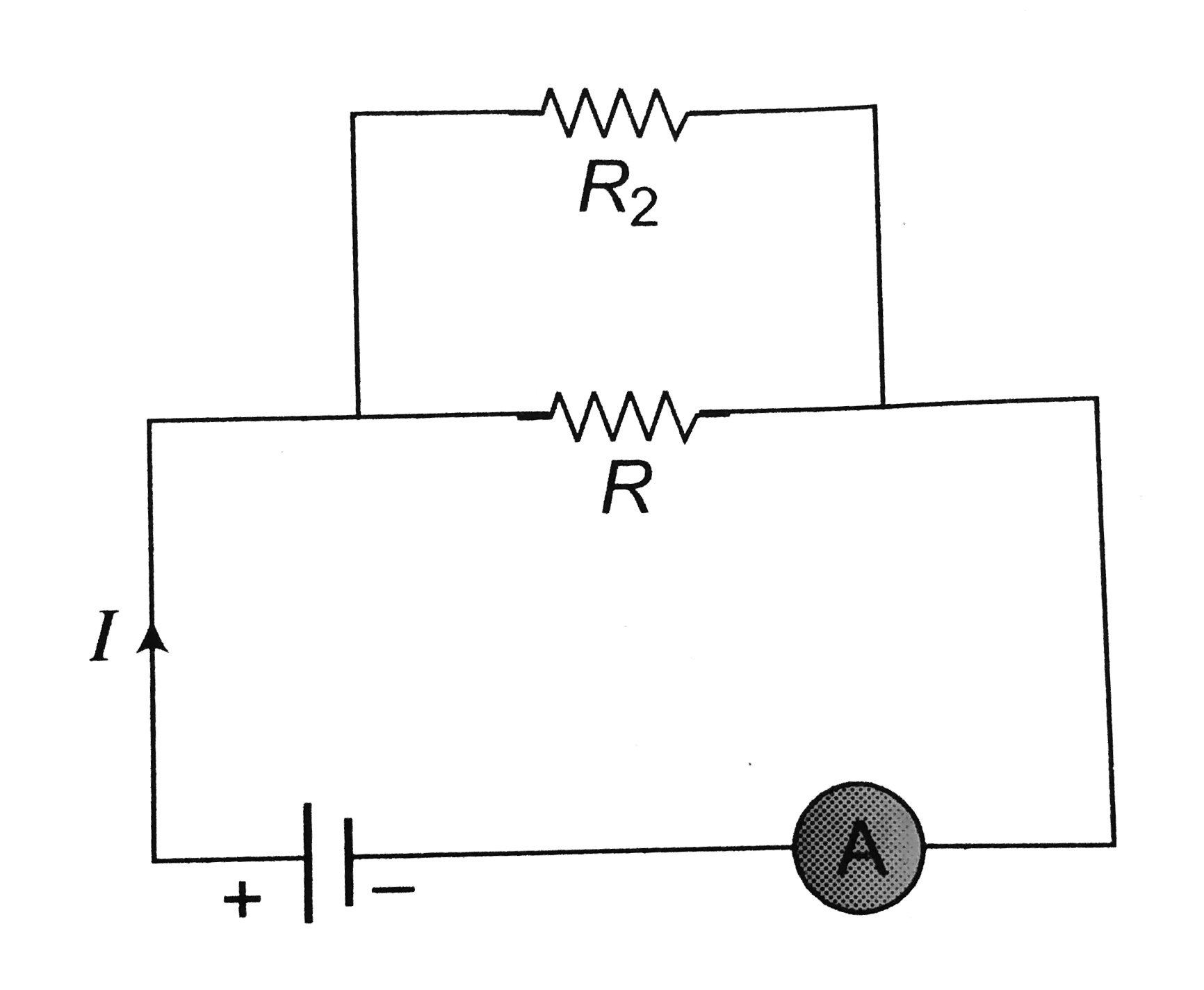 AI3,RBI.2RCI3,2RDI2,R
AI3,RBI.2RCI3,2RDI2,R
Two conductors of resistance R1(50±2) ohm and R2=(100±4) ohm are connected in (a) series and (b) parallel. Find the equivalent resistance.
View SolutionTwo resistance R1=100±3ΩandR2=200±4Ω are connected in seriesg. What is their equivalent resistance?
View SolutionA galvanometer of resistance G is converted into a voltmenter to measrue upto V volts by connecting a resistance R1 in series with the coil. If a resistance R2 is connected series with it, then it can measure upto 1//2 volts. Find the resistance, in terms of R1 and R2, required to be connected to convert in into a voltmeter that can read upto 2V. Also find the resistance G of the galvanometer in terms of R1 and R2
View SolutionA resistance R1 is connected to a source of constant voltage . On connecting a resistance R2 in series with R1
View SolutionA coil of some internal resistance 'r' behaves line an inductance. When it is connected in series with a resistance R1, the time constant is found to be τ1. When it is connected in series with a resistance R2, the time constant is found to be τ2. The inductance of the coil is
View Solution
