Two parallel plane mirrors M1andM2 have a length of 2 m each and are 10 mm apart. A ray of light is incident on one end of mirror M2 at an angle of 30∘. The number of reflections light undergoes before reaching the other end is –
346
134
80
173
The correct Answer is:A
To solve the problem of how many reflections a ray of light undergoes before reaching the other end of the mirror, we can follow these steps:
1. Understanding the Geometry:
- We have two parallel mirrors, M1 and M2, each of length 2 m (2000 mm).
- The distance between the mirrors is 10 mm.
2. Identify the Angle of Incidence:
- The ray of light is incident at an angle of 30∘ to the normal at the end of mirror M2.
3. Calculate the Vertical Distance (h):
- We need to find the vertical distance (h) that the light travels before it reflects off the opposite mirror.
- Using the tangent of the angle of incidence:
tan(30∘)=h10 mm
- Since tan(30∘)=1√3, we can write:
1√3=h10 mm⟹h=10 mm√3≈5.77 mm
4. Convert Units:
- Convert h to meters for consistency:
h=5.77 mm=5.77×10−3 m
5. Calculate the Number of Reflections:
- The total length of the mirror is 2 m (2000 mm).
- The number of reflections can be calculated by dividing the total length of the mirror by the vertical distance (h):
Number of reflections=Total Lengthh=2 m5.77×10−3 m≈346
Final Answer:
The number of reflections the light undergoes before reaching the other end is approximately 346.
---
- We have two parallel mirrors, M1 and M2, each of length 2 m (2000 mm).
- The distance between the mirrors is 10 mm.
- The ray of light is incident at an angle of 30∘ to the normal at the end of mirror M2.
- We need to find the vertical distance (h) that the light travels before it reflects off the opposite mirror.
- Using the tangent of the angle of incidence:
tan(30∘)=h10 mm
- Since tan(30∘)=1√3, we can write:
1√3=h10 mm⟹h=10 mm√3≈5.77 mm
- Convert h to meters for consistency:
h=5.77 mm=5.77×10−3 m
- The total length of the mirror is 2 m (2000 mm).
- The number of reflections can be calculated by dividing the total length of the mirror by the vertical distance (h):
Number of reflections=Total Lengthh=2 m5.77×10−3 m≈346
The number of reflections the light undergoes before reaching the other end is approximately 346.
Topper's Solved these Questions
Similar Questions
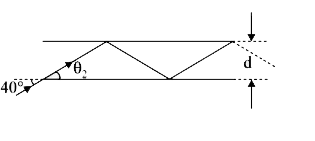
In figure, the optical fiber is l = 2 m long and has a diameter of d=20μm. If a ray of light is incident on one end of the fiber at angle θ1=40∘ , the number of reflections it makes before emerging form the other end is close to : (refractive index of fiber is 1.31 and sin40∘=0.64)
View SolutionA ray of light is incident on a plane mirror at an angle of 40∘ with respect to surface normal. When it gets reflected from the mirror, it undergoes a deviation of
View Solution
Knowledge Check
Two plane mirrors M1 and M2 each have length 1m and are separated by 1cm. A ray of light is incident on one end of mirror M1 at angle 45∘. How many reflections the ray will have before going from the other end?
 A50B51C100D101
A50B51C100D101If a ray of light incident on a plane mirror is such that it makes an angle of 30∘ with the mirror, then the angel of reflection is
A30∘B45∘C55∘D60∘A ray of light is incident at an angle of 30∘ with the plane of a plane mirror. Find the angle of reflection.
A0∘B90∘C30∘D60∘
Two mirrors meet at right angles. A ray of light is incident on one at an angle of 30° as shown in Draw the reflected ray from the second mirror.

View SolutionIf a ray of light incident on a plane mirror is such that it makes an angle of 30∘ with the mirror, then the angle of reflection is
View SolutionTwo plane mirror M1andM2 are inclined to each other at 70∘. A ray incident on the mirror M1 at an angle θ fallls on M2 and is then reflected parallel to M1 for
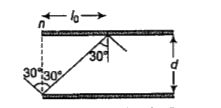
View SolutionThe mirrors each 1.6 m long are facing each other, The distance between the mirrors is 20 cm. A light ray is incident on one end of the mirror at an angle of incidence of 30∘ . How many times is the ray reflected before it reaches the other end?
View SolutionTwo plane mirrror are inclined to each other at 70∘. A ray of light is incident on one mirror. They ray after two reflections will undergo a total deviation of :
View Solution
