Question

A hypothetical planet of mass $M$ has three moons each of equal mass 'm' each revolving in the same circular orbit of radius $R$. The masses are equally spaced and thus form an equilateral triangle. Find :

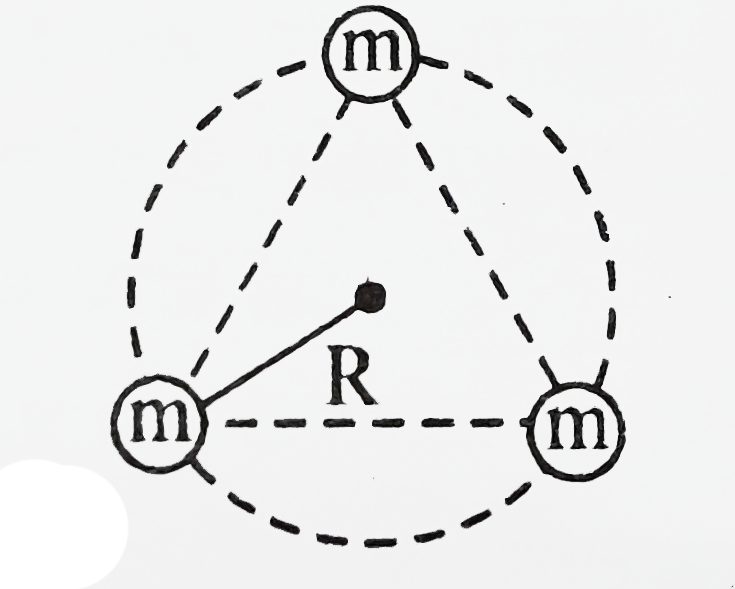
(i) the total $P.E.$ of the system
(ii) the orbital speed of each moon such that they maintain this configuration.

Answer

(i) `-(3Gm)/(R )((m)/(sqrt(3))+M)`, (ii) `sqrt((G)/(R )((m)/(sqrt(3))+M))`

Explanation

(i) U = Potential energy of (1) in the field M + potential energy of (2) in field of
`[(1)+M]+` Potential energy of (3) in field of `[(1)+(2)+M]`
`U=-(GMm)/(R )+m[-(GM)/(R )-(Gm)/(sqrt(3))]+m[-(GM)/(R )-(Gm)/(sqrt(3)R)-(Gm)/(sqrt(3)R)]`
`=-(3Gm)/(R )(3Gm^(2))/(sqrt(3)R)`
`=-(3Gm)/(R )[M+(m)/(sqrt(3))]`

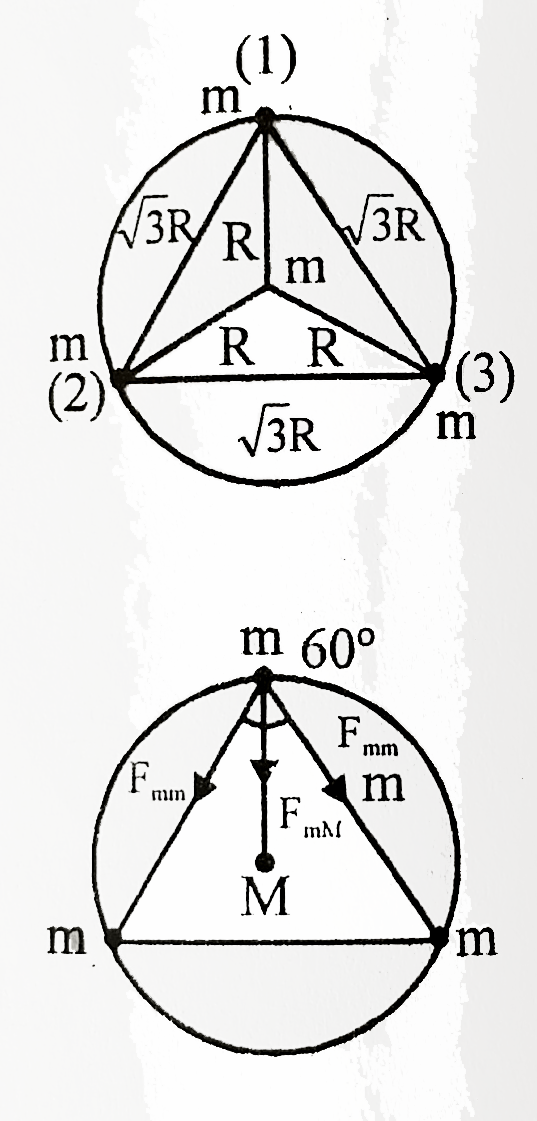
(ii) `F_(R )=F_(mM)+2F_(mm)cos 30^(@)`
`F_(R )=(Gm)/(R^(2))+sqrt(3)(Gm^(2))/((sqrt(3)R)^(2))`
`F_(R )=(Gm)/(R^(2))[M+(m)/(sqrt(3))]`
This force will provide required centrepetal force
`(mv^(2))/(R )=(Gm)/(R^(2))[M+(m)/(sqrt(3))] rArr v = sqrt((G)/(R )(M+(m)/(sqrt(3))))`