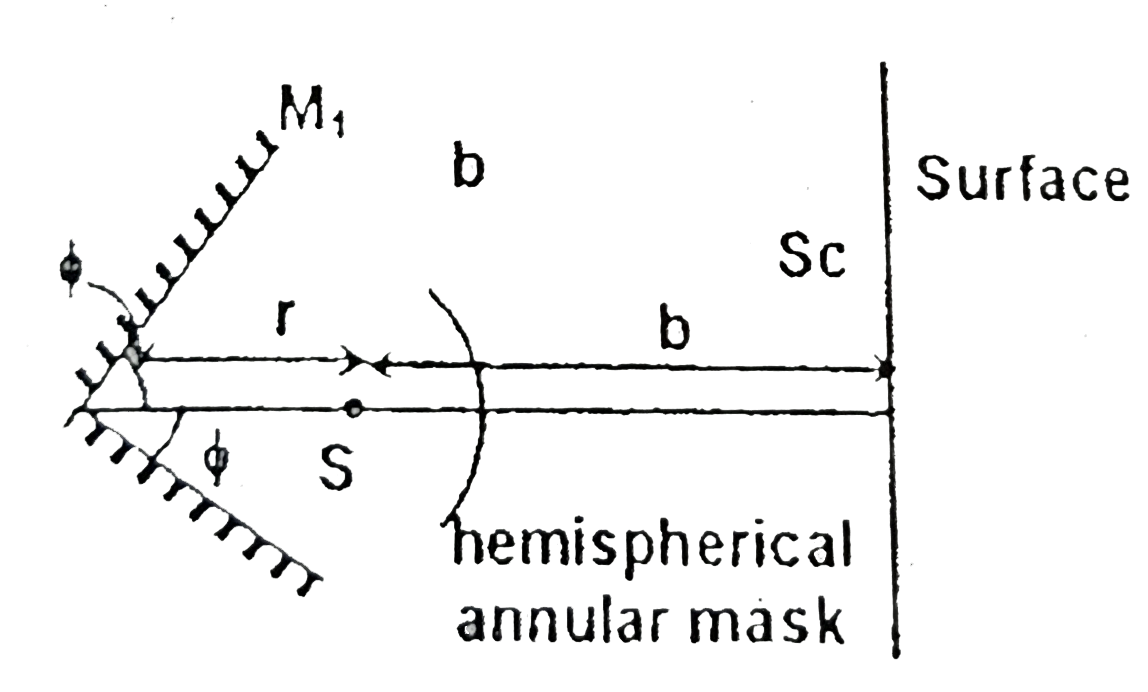
Two mirror $M_{1}$ and $M_{2}$ make an angle $ϕ$ with line $A B$ . A point source $S$ is kept at a distance $r$ from the point of intersection of mirror. A small hemispherical annular mask is kept close to $S$ so that no ray emanting from $S$ directly reaches the screen kept at a distance $b$ from the source. Interference pattern of rays reflected from $M_{1}$ and $M_{2}$ is oberved on the screen. Find the fringe width of this interference pattern $λ =$ wavelength of light being emitted by source.

$\frac{λ (b + 2 r {sin}^{2} ϕ)}{2 r sin 2 ϕ}$

$\frac{λ (b + 2 r cos 2 ϕ)}{2 r sin 2 ϕ}$

$\frac{λ (b + r cos 2 ϕ)}{2 r sin 2 ϕ}$

$\frac{λ (b + 2 r cos 2 ϕ)}{r sin 2 ϕ}$

Video Solution

Text Solution

Verified by Experts

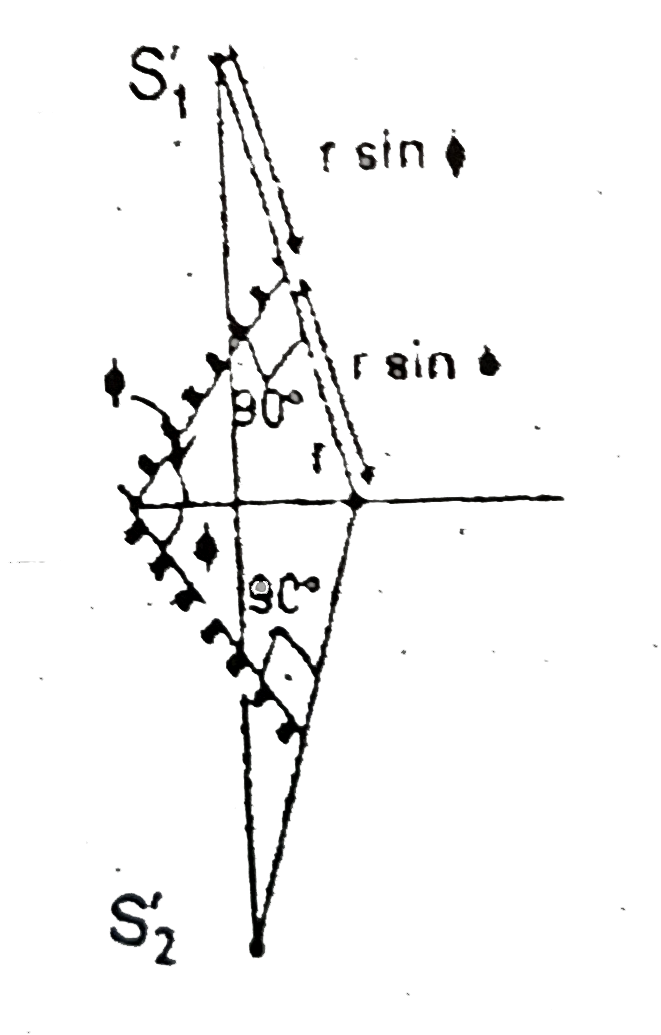
All light rays hitting the screen will be appearing to be coming from $S'_{1}$ and $S'_{2}$
$\Rightarrow D = b + 2 r {sin}^{2} ϕ$
$d = 4 r sin ϕ cos ϕ$
fringe width $= \frac{λ D}{d}$

Updated on:21/07/2023

The distance between two coherent sources is 1 mm. The screen is placed at a distance of 1 m from the sources. If the distance of the third bright fringe is $1.2$ mm from the central fringe, the wavelength of light used is
A $4000 Å$
B $5000 Å$
C $6000 Å$
D $7200 Å$
Two bodies of masses m and 2m are kept at distance r apart from each other. Then the value of G varies as
A $r^{2}$
B $r^{4}$
C $r^{- 2}$
D $r^{t h}$
The sound level at a point 5-0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source ?
A26 dB
B16dB
C23dB
D32dB