Question

The minimum distance between an object and its real image formed by a thin convex lens of focal length $f$ is $K.f$. Find the value of $K$.

Explanation

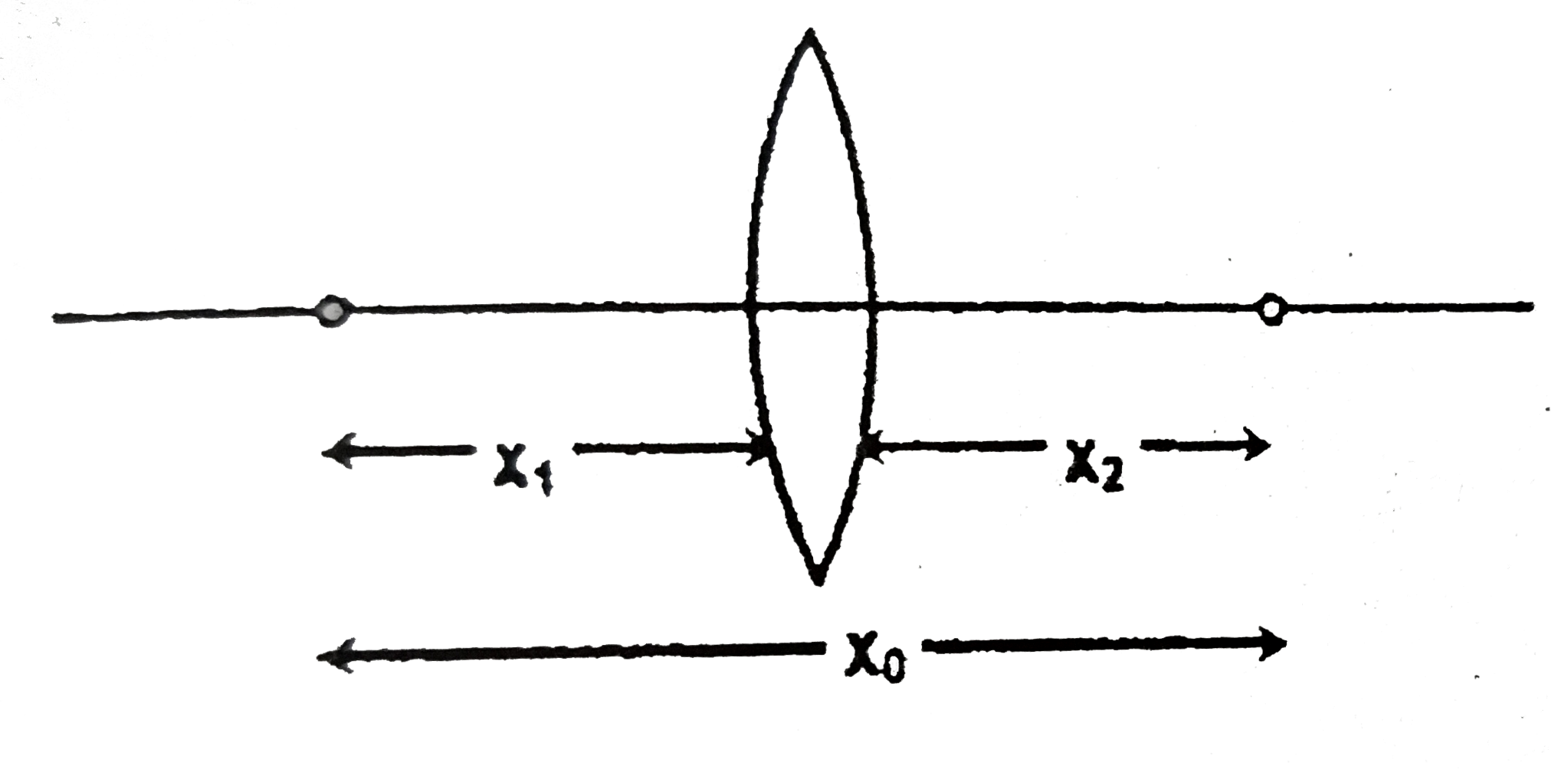
Since object and image is real
then object distance `= -x_(1)`
Image distance `=x_(2)`
`x_(0)=x_(1)+x_(2)`, `(1)/(x_(2))-(1)/(-x_(1))=(1)/(f)`
`rArr x_(1)+x_(2)=(x_(1)x_(2))/(f)`
`rArr d=(x_(1)(x_(1)-d))/(f)`
`rArrx_(0)=(x_(1)^(2))/(x_(2)-f)(dx_(0))/(dx_(1))=0`
`rArr x_(1)=2f`
which means `x_(2)=2f`
distance between object and image is `4f`