A uniformly conducting wire is bent to form a ring of mass 'm' and radius 'r', and the ring is placed on a rough horizontal surface with its plane horizontal. There exists a uniform and constant horizontal magnetic field of induction B. Now a charge q is passed through the ring in a very small time interval Δt. As a result the ring ultimately just becomes vertical. Calculate the value of g(acceleration due to gravity) in terms of other given quantities. Assume that friction is sufficient to prevent slipping and ignore any loss in energy.
Angular momentum, (32mr2)ω=∫τdt=∫dqdtπr2Bdt=qπr3B
For the ring to become vertical,
12(32mr2)ω2=mgr
i.e. g=π23(qBm)2r
Topper's Solved these Questions
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Objective problems
Explore 215 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Assertion & Reason
Explore 15 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
Similar Questions
A conducting ring of mass 2 kg and radius 0.5 m is placed on a smooth horizontal plane. The ring carries a current 4A . A horizontal magnetic field B = 10T is switched on at time t = 0 as shown in figure. The initial angular acceleration of the ring will be:

View SolutionA uniform ring of mass M and radius R carries a current I (see figure). The ring is suspended using two identical strings OA and OB. There exists a uniform horizontal magnetic field B0 parallel to the diameter AB of the ring. Calculate tension in the two strings. [Given θ=60∘]

View Solution
Knowledge Check
A force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
 AF2 towards rightBF3 towards leftC2F3 towards rightDZero
AF2 towards rightBF3 towards leftC2F3 towards rightDZeroA ring of mass m and radius R rolls on a horizontal roudh surface without slipping due to an applied force 'F'. The frcition force acting on ring is :−
 AF3B2F3CF4DZero
AF3B2F3CF4DZeroAn impulse J is applied on a ring of mass m along a line passing through its centre O. The ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without slipping is
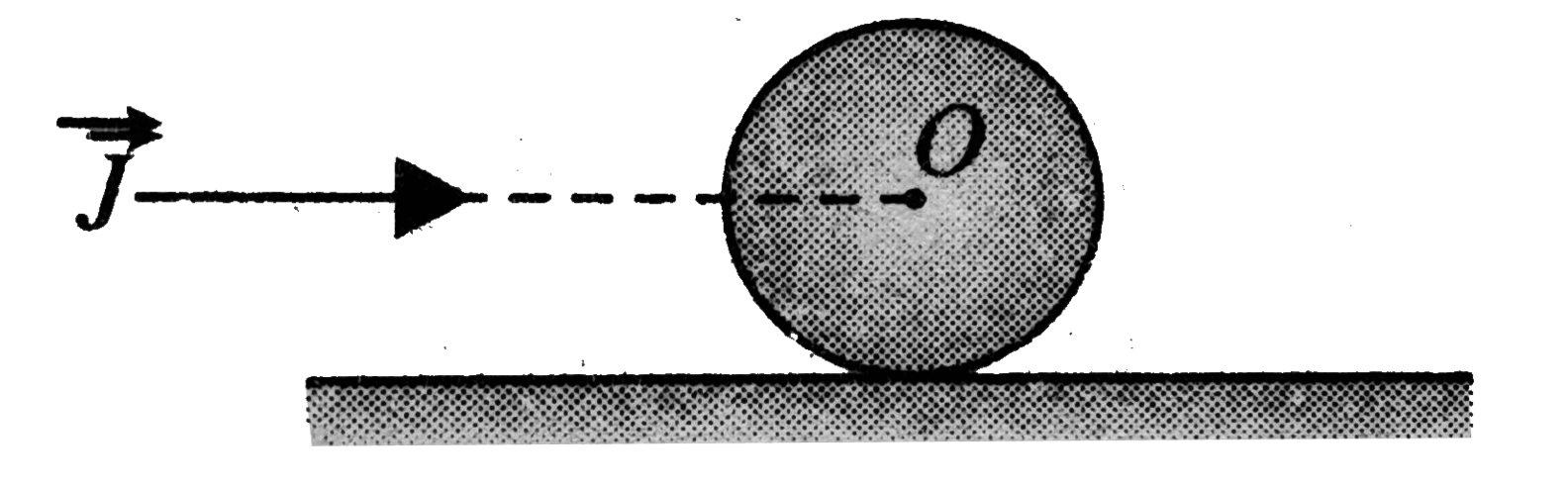 AJ/mBJ/2mCJ/4mDJ/3m
AJ/mBJ/2mCJ/4mDJ/3m
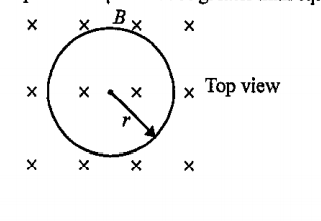
A nonconducting ring (of mass m, radius r, having charge Q) is placed on a rough horizontal surface (in a cylindrical region with transverse magnetic field). The field is increasing with time at the rate R and coefficient of friction between the surface and the ring is μ. For ring to remain in equilibrium μ should be greater than equal to,
View SolutionA conducting ring of radius 2R rolls on a smooth horizontal conducting surface as shown in figure-5.295. A uniform horizontal magnetic field B is perpendicular to the plane of the ring. The potential of A with respect to O is:

View SolutionA thin wire is bent in the form of a ring of diameter 3.0cm.The ring is placed horizontally on the surface of soap solution and then raised up slowly. Upward force necessary to break the vertical film formed between the ring and the solution is
View SolutionA ring of mass m and radius R is rolling down on a rough inclined plane of angle θ with horizontal. Plot the angular momentum of the ring about the point of contact of ring and the plane as a function of time
View SolutionA conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
View Solution

