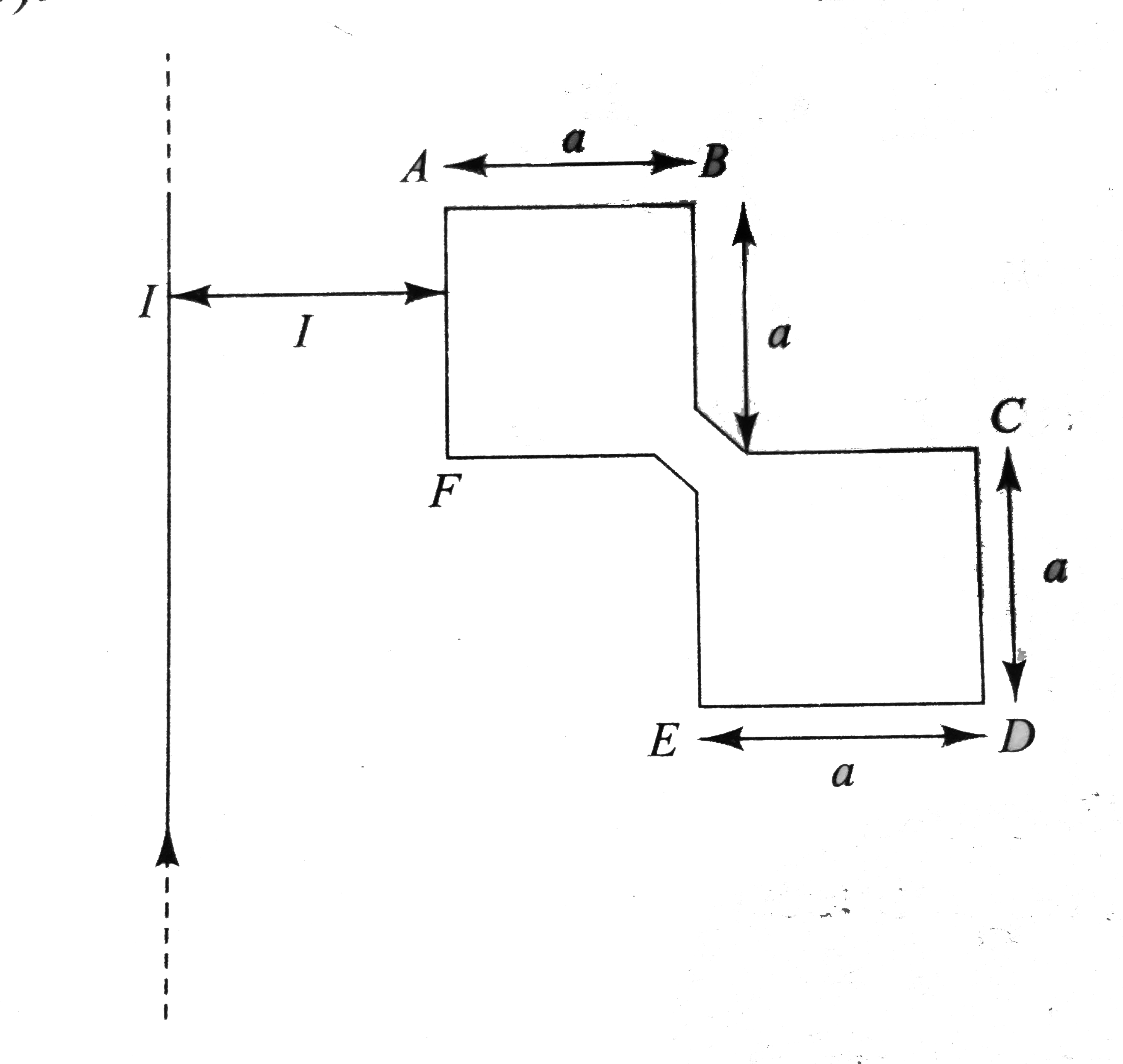
In Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).
The heat produced in the loop in time t is
(a) Consider a strip at a distance x from the wire of thickness dx.
Magnetic flux associated with this strip Δϕ=B(x)adx=μ0Ia2πxdx
⇒ϕ=μ0Ia2π[∫a+lldxx−∫2a+la−ldxx]=μ0Ia2πln((a+l)2a(2a+l))
∵M=ϕI(primary)
⇒M=μ0a2πln((a+l)2)a(2a+l)
(b) ε=−MdIdt
⇒ε=−MI0
Heat produced =ε2Rt=[μ02πln(a+l)2a(2a+l)I0]2at8λ

Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Objective problems
215 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
Knowledge Check
In Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).

The emf induced in the closed loop isAμ0I0a2πIn(2a+ll)Bμ0I0a2πIn(2a−ll)Cμ0I0aπIn(a+ll)Dμ0aπIn(a+ll)In Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).

The mutual inductance of the pair isAμ0a2πIn(2a+ll)Bμ0a2πIn(2a−ll)Cμ0aπIn(a+ll)Dμ0aπIn(a+ll)A current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is
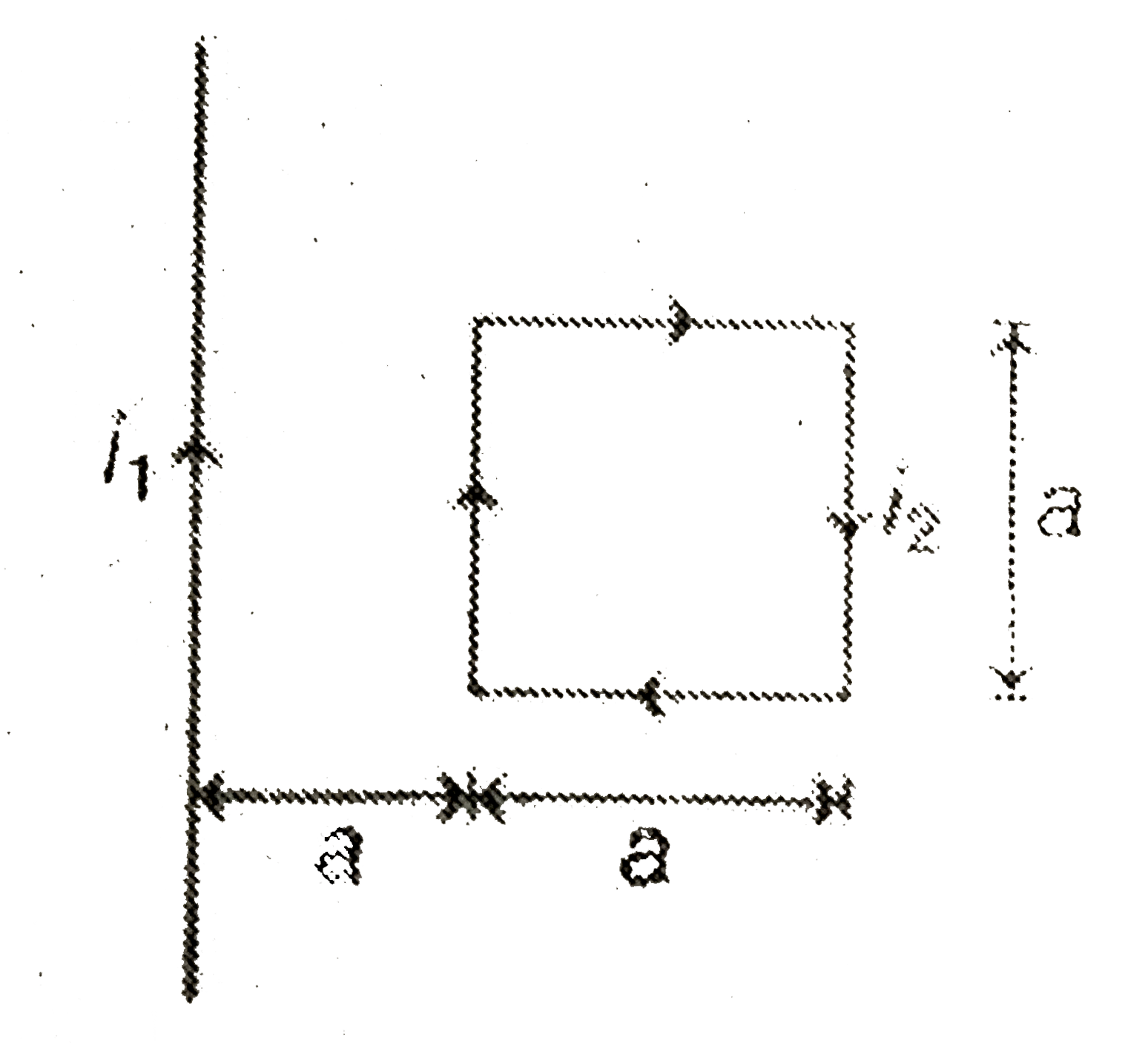 Aμ02πi1i2rBμ02πi1i2loge2Cμ02πi1i2r2DZero
Aμ02πi1i2rBμ02πi1i2loge2Cμ02πi1i2r2DZero
Figure shows a conducting loop placed near a long straight wire carrying a current i as shown, if the current increases continuously, find the direction of the induced current in the loop.

View SolutionA rectangular loop carryinig current I is located near an infinite long straight conductor carrying current I as shown in the figure. The loop,

View SolutionA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is

View SolutionA long straight wire is parallel to one edge of a rectangular loop as shown in figure-5.310. if the current in the long wire varies with time as I=I0e−tr, what will be the induced emf in the loop at t=τ?

View SolutionA loop and an infinite wire are placed side by side as shown in the figure. If the current I in the wire is increased then the induced current in the loop is
View Solution