Block B has a downward velocity in $m / s$ and given by $v_{B} = \frac{U^{2}}{2} + \frac{U^{3}}{6}$ , where t is in s. Acceleration of A at $t = 2$ second is

A

$2 m / s^{2}$

B

$4 m / s^{2}$

C

$6 m / s^{2}$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

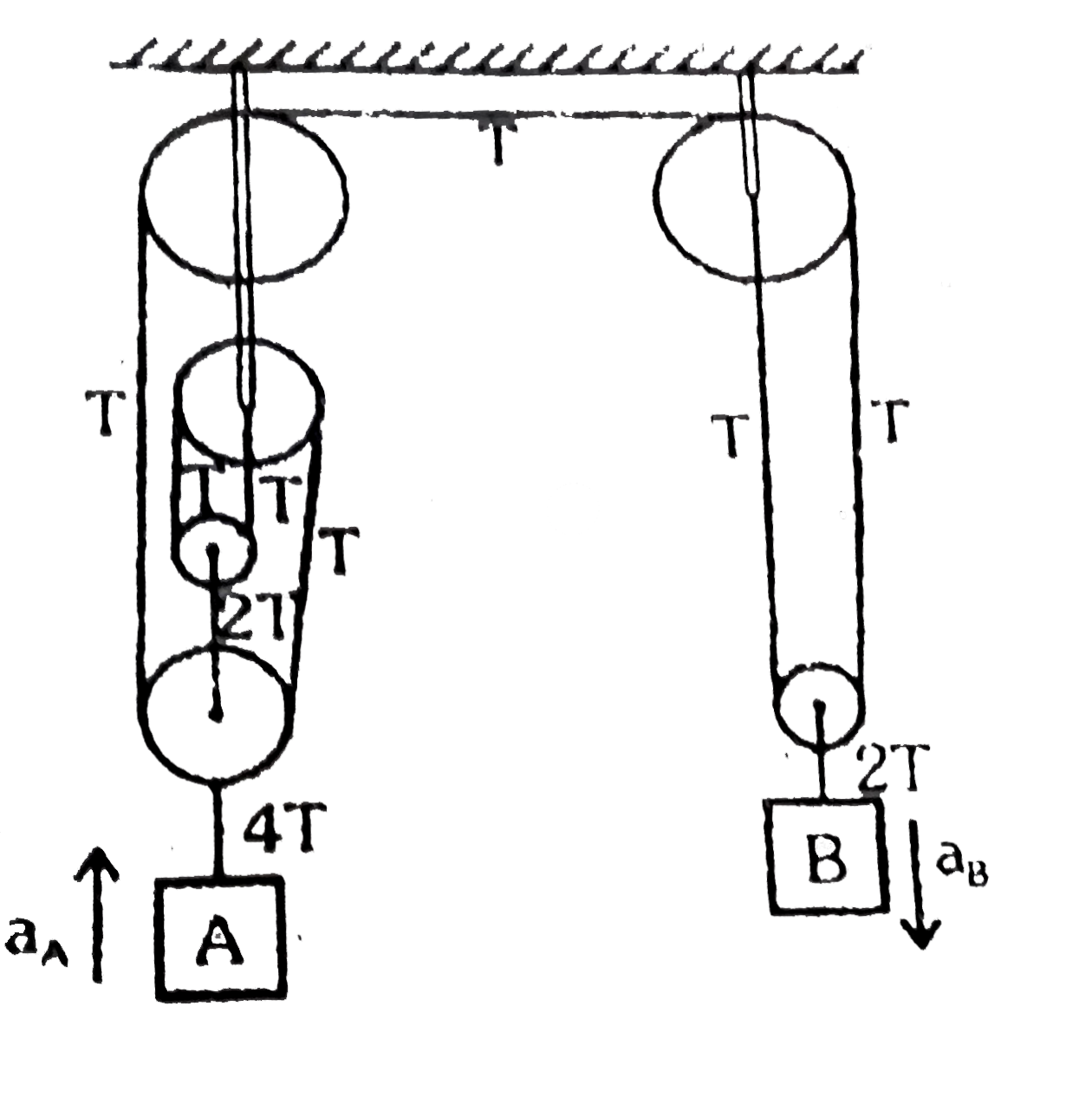
$(4 T) a_{A} = (2 T) (a_{B})$
$\Rightarrow a_{A} = \frac{a_{B}}{2}$
but $a_{B} = \frac{d v_{B}}{d t}$
$= t + \frac{t^{2}}{2} \Rightarrow a_{A} = \frac{t}{2} + \frac{t^{2}}{4}$
At $t = 2 s$ ,
$a_{A} = \frac{2}{2} + \frac{{(2)}^{2}}{4} 1 + 1 = 2 m s^{- 2}$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $v = (t^{2} - 4 t + 10^{5})$ m/s where t is in second. Find acceleration at t=1 sec.
A0
B $2 m / s^{2}$
C $- 2 m / s^{2}$
DNone of these
Question 2 - Select One
If velocity of a particle is given by $v = 2 t^{2} - 2$ then find the acceleration of particle at t = 2 s.
A0
B2
C4
D8
Question 3 - Select One
If a man has a velocity varying with time given as $v = 3 t^{2}, v$ is in $m / s$ and $t$ in $sec$ then $:$

Find out his acceleration after 3 seconds $:$
A $9 m / s^{2}$
B $18 m / s^{2}$
C $12 m / s^{2}$
D $6 m / s^{2}$

ALLEN-KINEMATICS-EXERCISE-02

Home
Ask Doubt
Profile