A particle is projected from a point P with a velocity v at an angle with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
Velocity of particle at Q is
Velocity of particle at Q is
Time of flight from P to Q is
Time of flight from P to Q is
The correct Answer is:B, C
Horizontal component of velocity remains constant
(from figure)
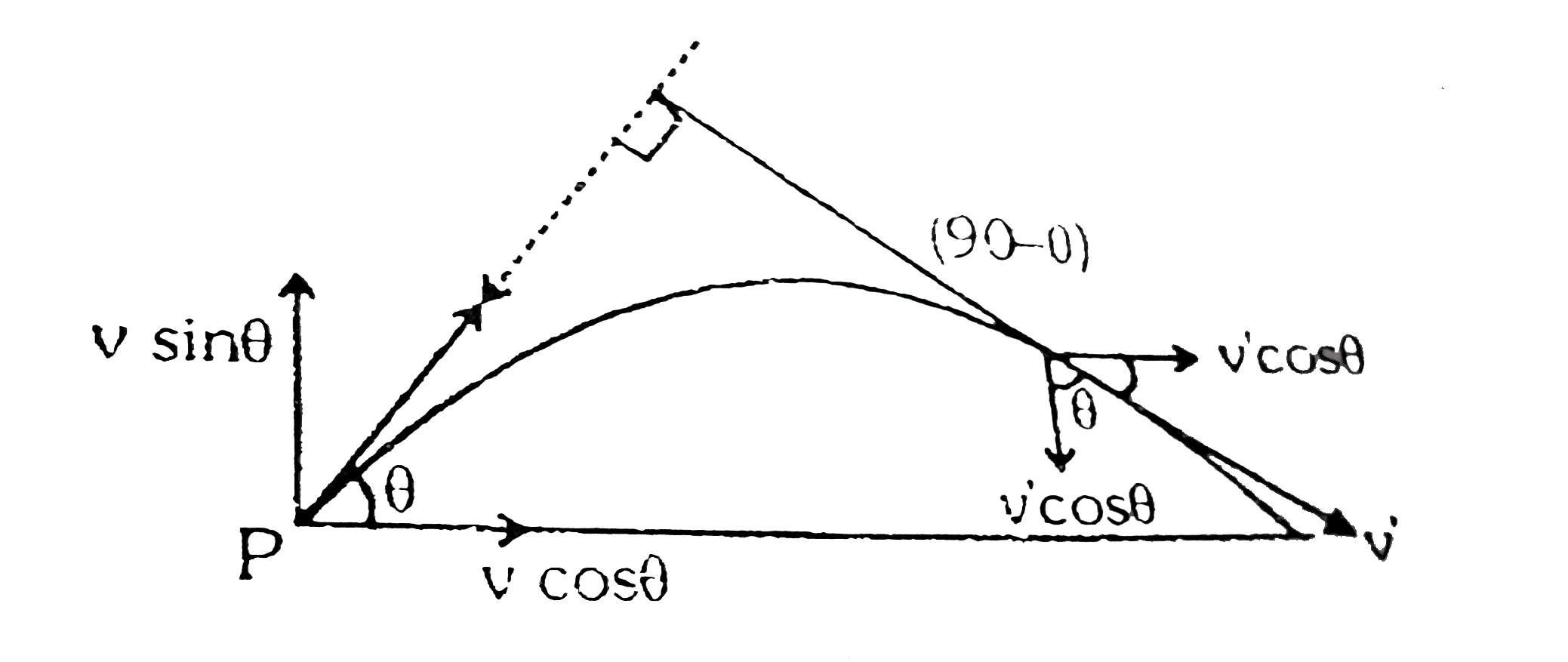
So from
Topper's Solved these Questions
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-03
Explore 6 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:Assertion-Reason
Explore 20 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-01
Explore 55 Videos
- ERROR AND MEASUREMENTBook:ALLENChapter:ERROR AND MEASUREMENTExercise:Part-2(Exercise-2)(B)
Explore 22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
Similar Questions
A particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.
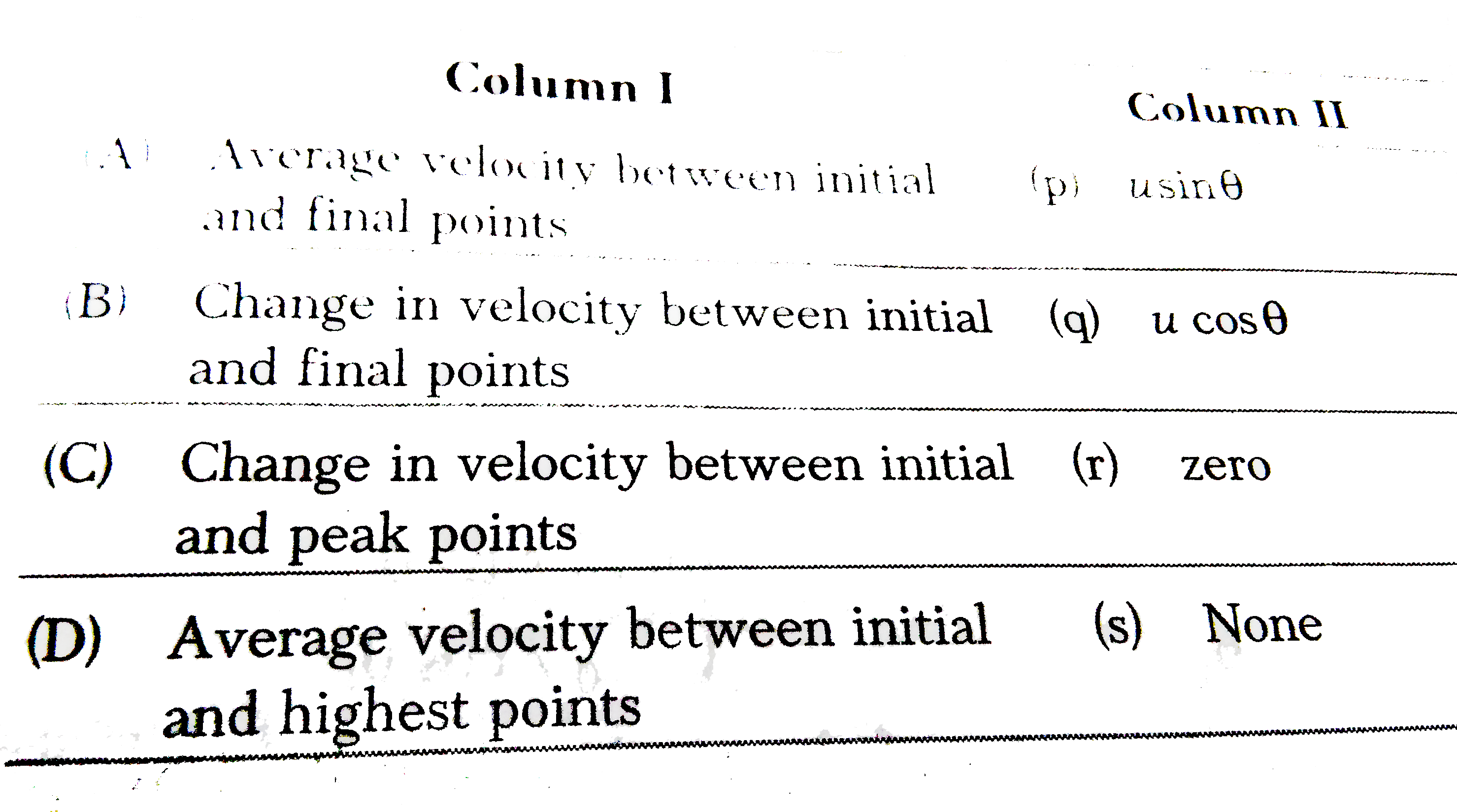
View SolutionA particle is projected from the ground with an initial speed v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectory is [EAM2013]
View Solution
Knowledge Check
A particle is projected from a point O with a velocity u at an angle α (upwards) to the horizontal. At a certain point P it moves at right angles to its initial direction. It follows that:
AOP makes an angle tan−1(u/2g) to the horizontalBthe distance of P from O is u/(2gsinα).Cthe time of flight from O to P is u/(gsinα)Dthe velocity of the particle at P is u cot αA particle is project d from point A with velocity u at an angle α with horizontal. In its parabolic path, at point P the particle is moving at right angles to its initial direction of projection. Its velocity at P is:
AutanαBucotαCucosαDucosecαA particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
Av2√1+2cos2θBv2√1+2cos2θCv2√1+3cos2θDvcosθ
A particle is projected with a velocity u making an angle θ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
View SolutionA particle is projected from a point A with velocity u√2 at an angle of 45∘ with horizontal as shown in the figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is
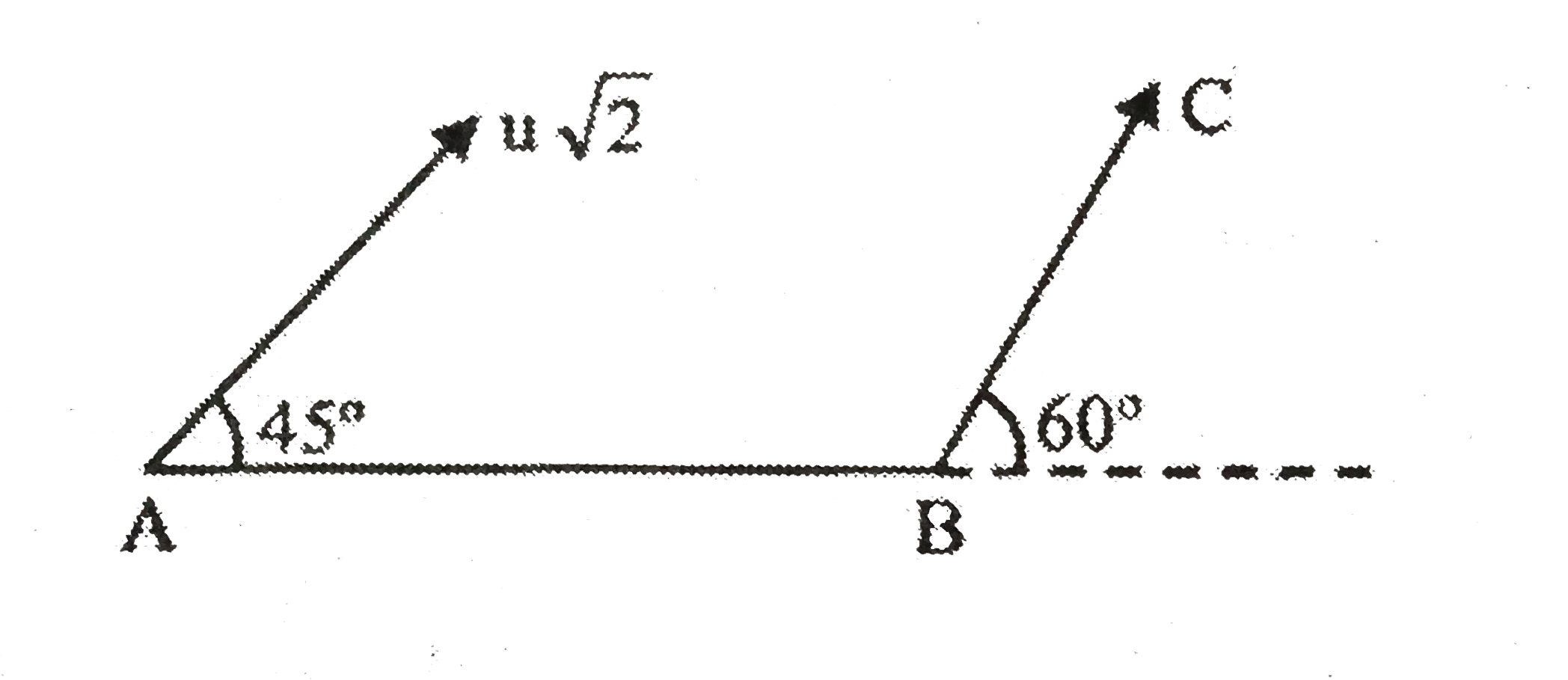
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionA particle is projected with a velocity of 39.2m/sec at an angle of 30∘ to the horizontal. It will move at right angles to the direction of projection after the time
View Solution

