Two particles P and Q are moving with velocity of $(ˆ i + ˆ j)$ and $(- ˆ i + 2 ˆ j)$ respectively. At time $t = 0$ , P is at origin and Q is at a point with positive vector $(2 ˆ i + ˆ j)$ . Then the shortest distance between P & Q is :-

A

$\frac{2 \sqrt{5}}{5}$

B

$\frac{4 \sqrt{5}}{5}$

C

$\sqrt{5}$

D

$\frac{3 \sqrt{5}}{5}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

${\to v}_{Q P} = - ˆ i + 2 ˆ j - ˆ i - ˆ j = - 2 ˆ i + ˆ j$

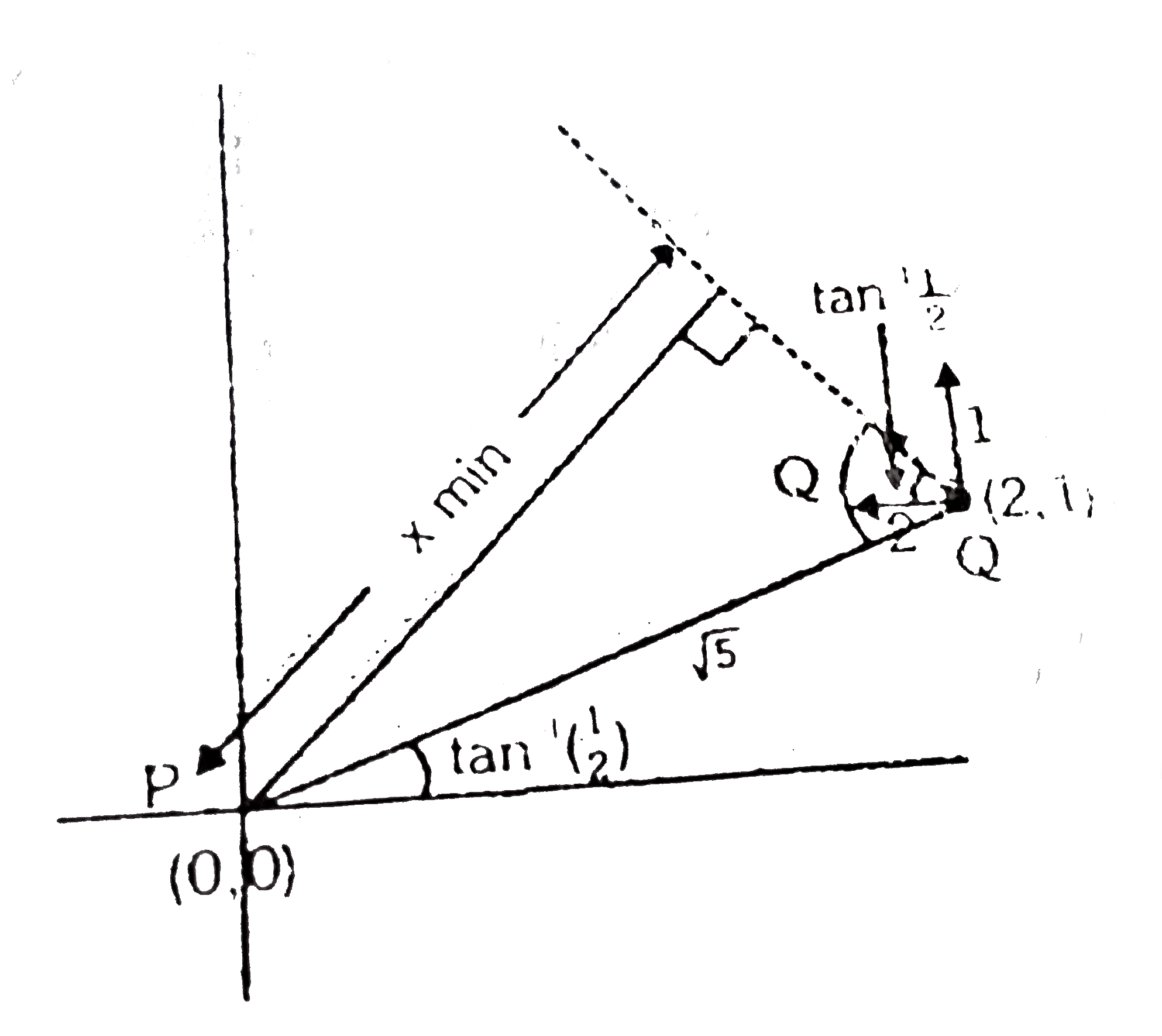
So from sine rule $\frac{\sqrt{5}}{{sin 90}^{\circ}} = \frac{x_{min}}{sin θ} \Rightarrow x_{m}$
$= \sqrt{5} \times 2 sin \frac{θ}{2} cos \frac{θ}{2}$
$= \sqrt{5} \times 2 \times \frac{1}{\sqrt{5}} \times \frac{2}{\sqrt{5}} = \frac{4}{\sqrt{5}}$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
If $\to A = 2 ˆ i + ˆ j + ˆ k$ and $\to B = ˆ i + ˆ j + ˆ k$ are two vectors, then the unit vector is
APerpendicular to $\to A$ is $(- ˆ j + ˆ k) \frac{1}{\sqrt{2}}$
BParallel to $\to A$ is $\frac{2 ˆ i + ˆ j + ˆ k}{\sqrt{6}}$
CPerpendicular to $\to B$ is $(\frac{- ˆ j + ˆ k}{\sqrt{2}})$
DParallel to $\to A$ is $\frac{ˆ i + ˆ j + ˆ k}{\sqrt{3}}$
Question 2 - Select One
The angle between the vectors $(ˆ i + ˆ j + ˆ k)$ and $(ˆ i - ˆ j - ˆ k)$ is
A ${sin}^{- 1} (\frac{\sqrt{8}}{3})$
B ${sin}^{- 1} (\frac{1}{3}) + \frac{π}{3}$
C ${cos}^{- 1} (\frac{\sqrt{8}}{3})$
D ${cos}^{- 1} \sqrt{\frac{8}{3}}$
Question 3 - Select One
If $\to P = ˆ i + ˆ j - ˆ k$ and $\to Q = ˆ i - ˆ j + ˆ k$ , then unit vector along $(\to P - \to Q)$ is $:$
A $\frac{1}{\sqrt{2}} ˆ i - \frac{1}{2} ˆ k$
B $\frac{\sqrt{2} ˆ j - \sqrt{2} ˆ k}{2}$
C $\frac{ˆ j - ˆ k}{2 \sqrt{2}}$
D $\frac{2 ˆ j - 2 ˆ k}{4}$

ALLEN-KINEMATICS-EXERCISE-01

Home
Ask Doubt
Profile