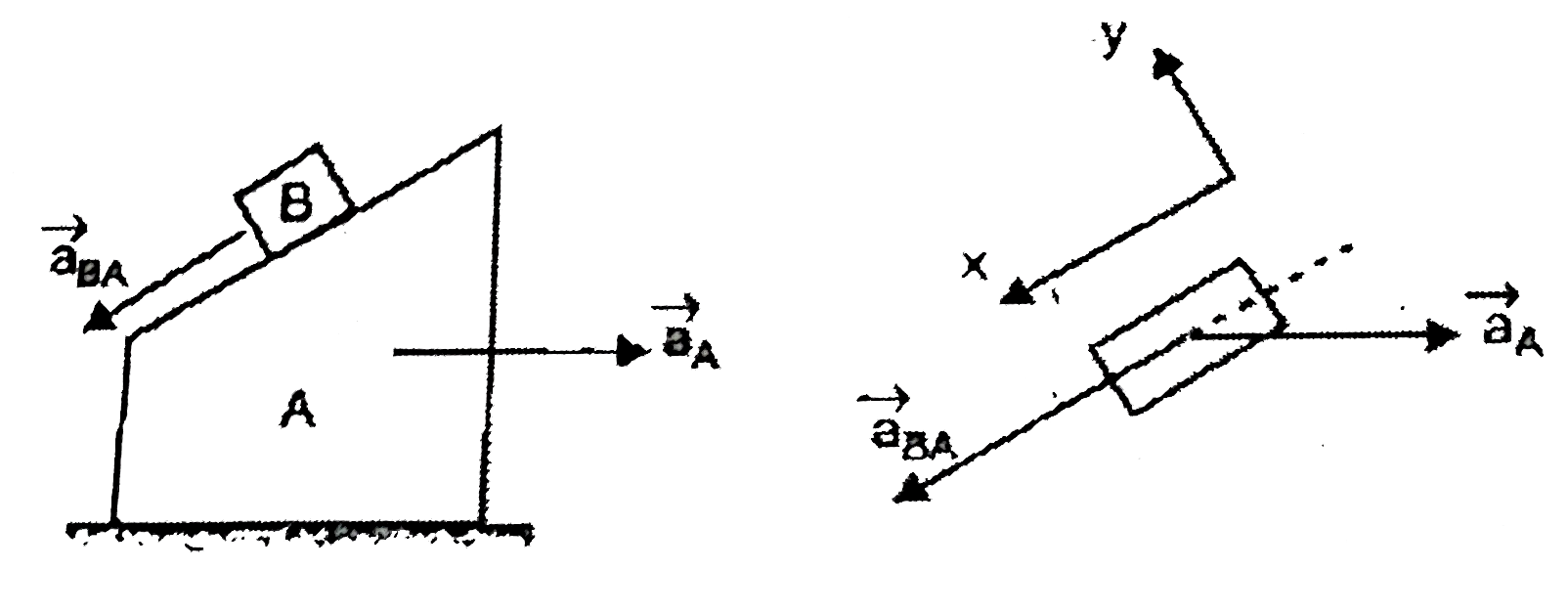
A weightless inextensible rope rests on a stationary wedge forming an angle α with a horizontal One end of the rope is fixed to the wall to point A.A small load is attached to the rope at point B The wedge starts moving to the right with a constant acceleration a The acceleration of the load is given by
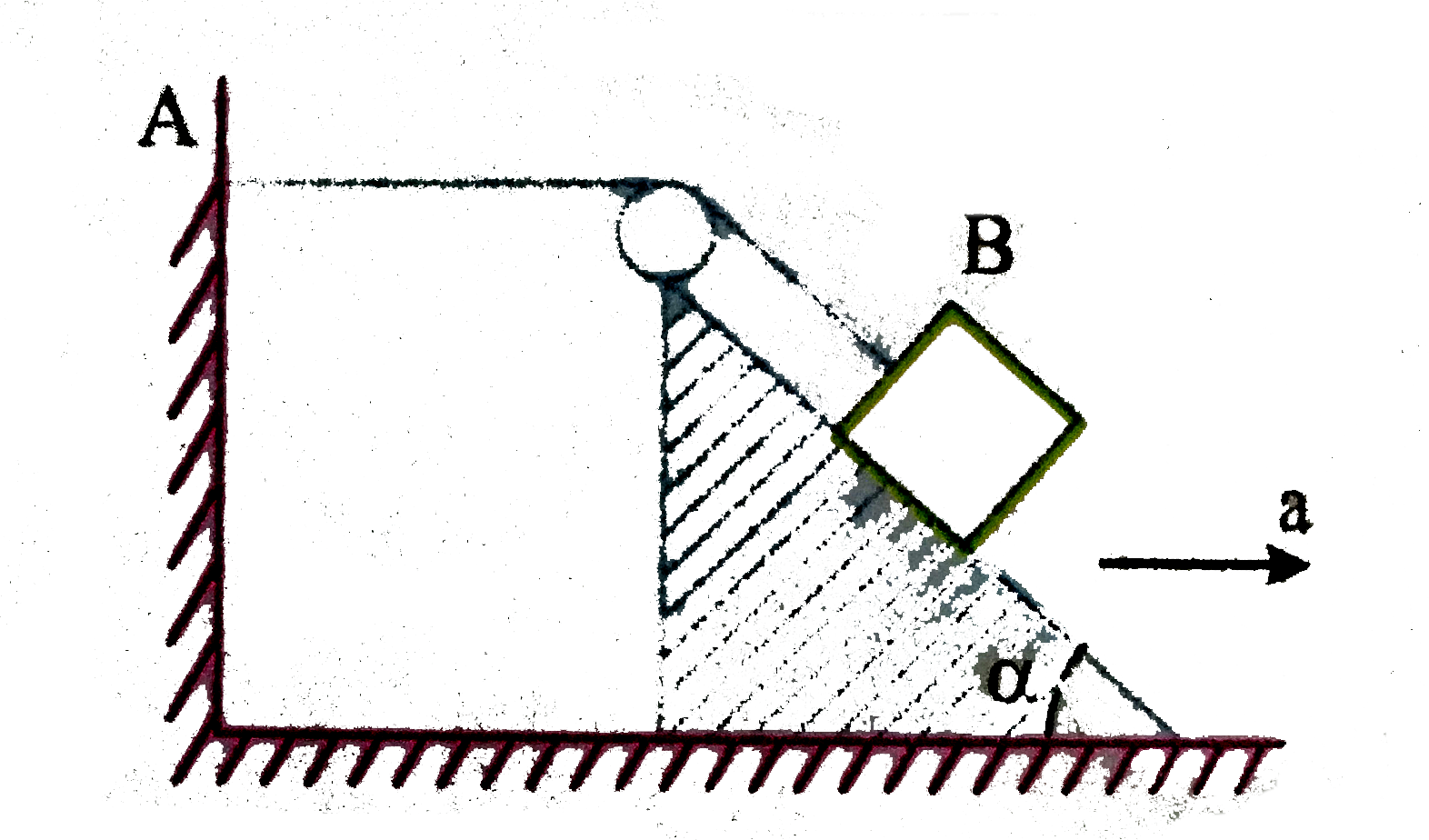 .
.
a
2asinα
2asinα2
gsinα
The correct Answer is:C
Net acceleration of load
=2acos(π−α2)=2asin(α2)

Topper's Solved these Questions
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-02
Explore 57 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-03
Explore 6 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:Integer Type Question
Explore 3 Videos
- ERROR AND MEASUREMENTBook:ALLENChapter:ERROR AND MEASUREMENTExercise:Part-2(Exercise-2)(B)
Explore 22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
Similar Questions
A homogeneous flexible rope rests on a wedge whose side edges make angles α and β with the horizontal. The central part of the rope lies on the upper rib C of the wedge. With what acceleration should the wedge be pulled to the left along the horizontal plane in order to prevent the displacement of the rope with respect to the wedge? [Consider all surfaces to be smooth]

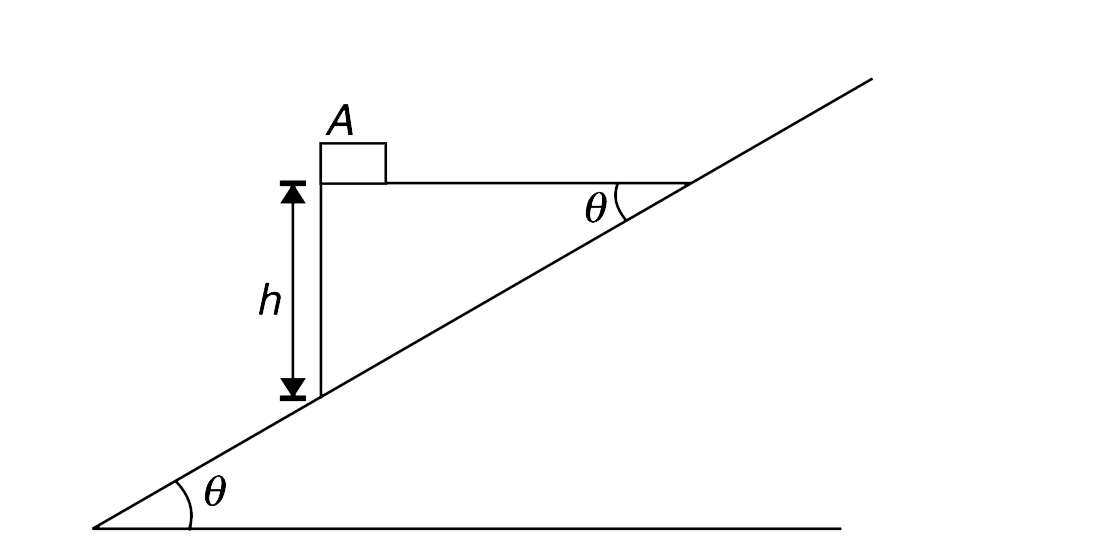
View SolutionA wedge is placed on the smooth surface of a fixed incline having inclination θ with the horizontal. The vertical wall of the wedge has height h and there is a small block A on the edge of the horizontal surface of the wedge. Mass of the wedge and the small block are M and m respectively.
(a) Find the acceleration of the wedge if friction between block A and the wedge is large enough to prevent slipping between the two.
(b) Find friction force between the block and the wedge in the above case. Also find the normal force between the two.
(c) Assuming there is no friction between the block and the wedge, calculate the time in which the block will hit the incline.
View Solution
Knowledge Check
A monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight and the tension of the rope for two cases .The monkey move downward with respect to the rope with an acceleration b.

The acceleration of weight isA2m(g+b)−μMgM+2mBm(g+b)−μMg2(M+m)Cm(g+b)−3μMgM+3mDm(g+b)−μMgM+2m
A block is placed on a smooth wedge of inclination angle θ with the horizontal. What minimum acceleration should be given to the wedge in the horizontal direction so that the block starts moving up along the incline?A>gcotθB>>anθC>gsinθD>gcosθA block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in the figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truj starts moving towards right with a constant acceleration a0. If the block is observed from the truck
 Athe block will execute SHMBthe time period of oscillations of block will be 2π√mkCthe amplitude of oscillation of block will be ma0kDthe energy of oscillations of block will be m2a20k
Athe block will execute SHMBthe time period of oscillations of block will be 2π√mkCthe amplitude of oscillation of block will be ma0kDthe energy of oscillations of block will be m2a20k
One end of a horizontal uniform beam of weight W and length L is hinged on a vertical wall at point O and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point Q at a height L above the hinge at point O. A block of weight αW is attached at the point Q at a height L above the hinge at point O. A block of weight αW is attached at the point P of the beam as shown in the figure. The rope can sustain a maximum tension of 2(√2)W. Which of the following statements is/are correct?
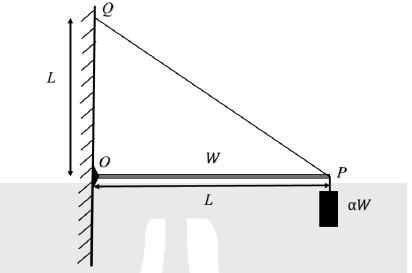
View SolutionA uniform rope of mass m and length L is attached to the ceiling of a lift. The other end of the rope is attached to a block of mass M. The lift is moving up with a constant acceleration a0. Find the tension in the rope at a distance x from the ceiling as shown in the diagram.

View SolutionA wedge of mass M rests with one face in contact with horizontal , smooth surface . A particle of mass m is placed on the smooth face on it , inclined at an angle αto the horizontal and released . Find the velocity of the wedge and that of the particle relative to the wedge when the particle has slipped a distance x down the face of the wedge . Also calculate the acceleration of the wedge and that of the particle relative to the wedge and the smooth surface .
[Hint : Apply principal of conservation of momentum along the horizontal and energy conservation principle . See Example 8 )
View SolutionThe block B starts from rest and slides on the wedge A which can move on a horizontal surface, Neglecting friction, determine (a) the acceleration of wedge, (b) the acceleration of the block relative to the wedge.
View SolutionA monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight and the tension of the rope for two cases .The monkey move downward with respect to the rope with an acceleration b.

The tension of rope is
View Solution

