A mass is attached to a spring. The spring is stretched to by a force and refeased. After being released, the mass comes to rest at the initial equilibrium position. The coeffiecient of friction, , is

The correct Answer is:C
By using work energy theorm,
Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
- TEST PAPER 1Book:ALLENChapter:TEST PAPER 1Exercise:PHYSICS
Explore 11 Videos
Similar Questions
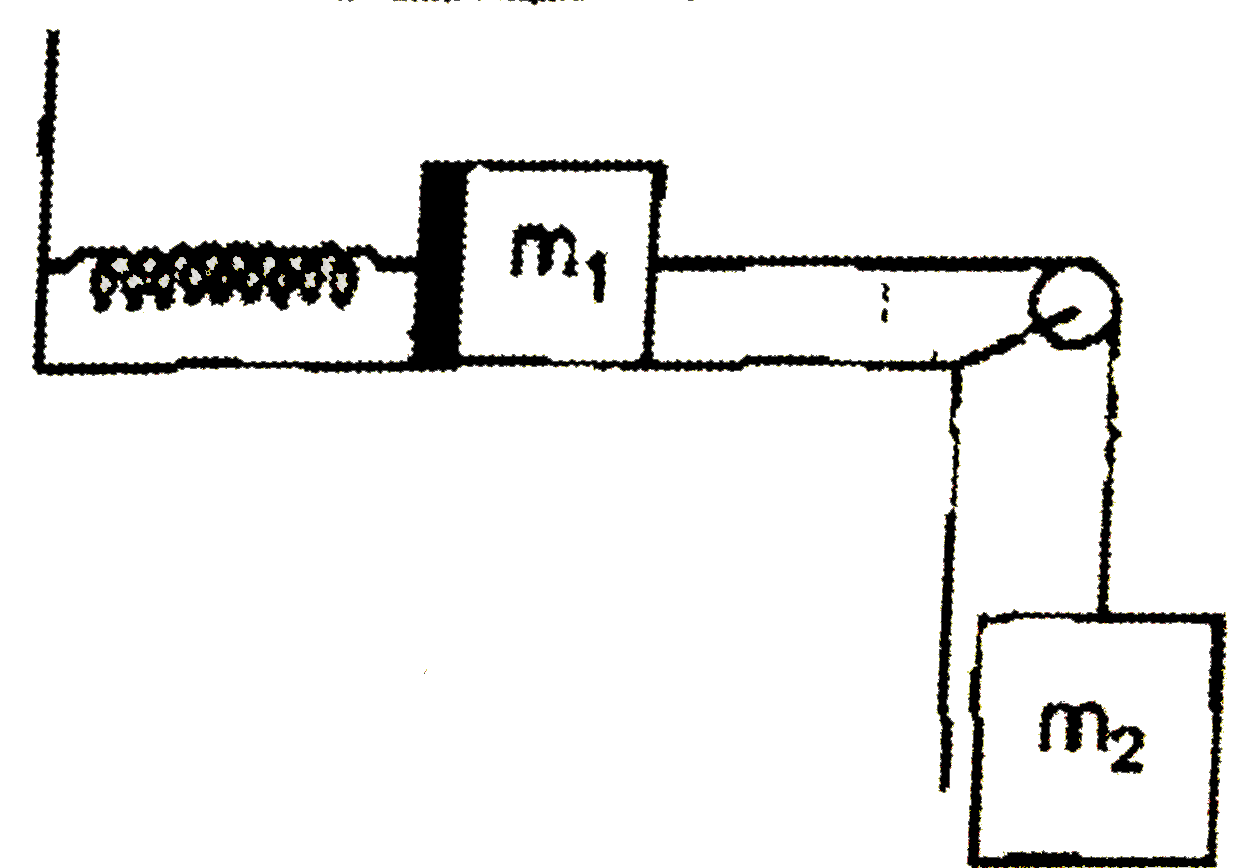
In Fig 3E.17, the mass m2 rests on a rough table. The mass m1 is pushed against the spring to which it is not attached Force constant of the spring is k, coefficient of friction is μk.
(a) Find the speed of the blocks after the spring is released and m2 has fallen a distance of h.
(b) If the spring is attached to the block and it falls a distance h before coming to rest, calculate the coefficient of friction μk.
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution
Knowledge Check
Two trolleys of mass m and 3m are attached by a spring. The spring was compressed and then released , they move off in opposite direction and comes to rest after covering distances s1 and s2 respectively. Assuming the coefficient of friction to be uniform , the ratio of distances s1:s2 is
A1:9B1:3C3:1D9:1A spring with one end attached to a mass and the other to a right support is stretched and released
AMagnitude of acceleration when just releases is maximumBMagnitude of acceleration, when at equilibrium position is maximumCspeed is maximum when mass is a equilibrium position.DMagnitude of displacement is always maximum whenever speed is minimumA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of these
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA sping of spring constant k is attached to the ceiling. A block of mass M is attached to its lower end and is released suddenly.
(ii) Find its speed at the instant it passes throught the equilibrium position.
View SolutionA mass m attached to a spring of spring constant k is stretched a distance x0 from its equilibrium position and released with no initial velocity. The maximum speed attained by mass in its subsequent motion and the time at which this speed would be attained are, respectively.
View SolutionA block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rfest with the spring velocity unstrached The maximum value praduced in the length of the spring will be
View SolutionConsider the system shown below, with two equal masses m and a spring with spring constant K. The coefficient of friction between the left mass and horizontal table is μ=1/4, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.
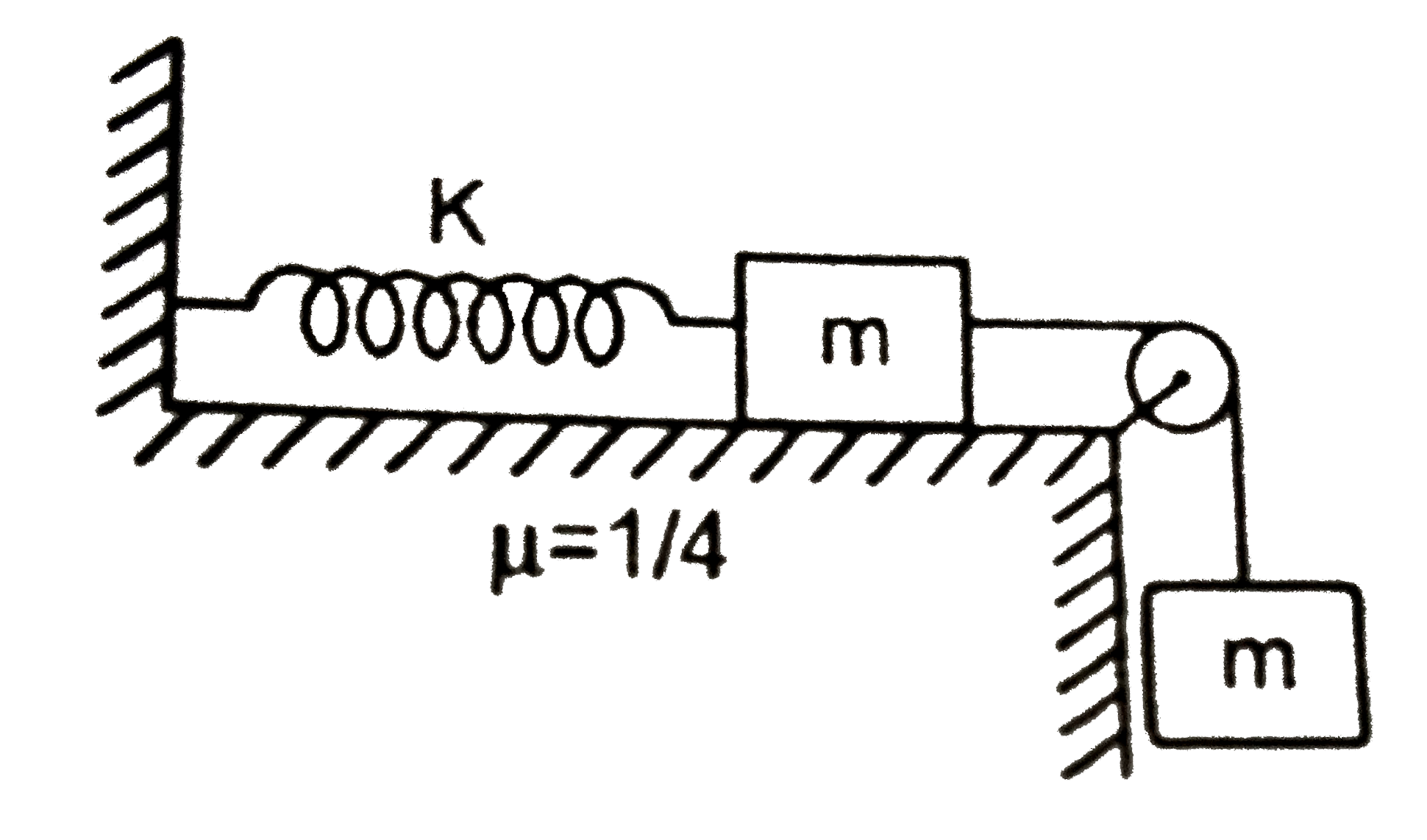
If the string connecting both the masses is cut just at the instant both masses came to momentary rest for the first time in question 5, then maximum compression of spring during resulting motion is (Take μ=1/4)
View Solution