As a particle moves along the x−axis, it is acted upon by a conservative force. The potential energy is shown below as a function of the coordinate x of the particle. Rank the labelled regions accoeording to the magnitude of force, least to greatest.
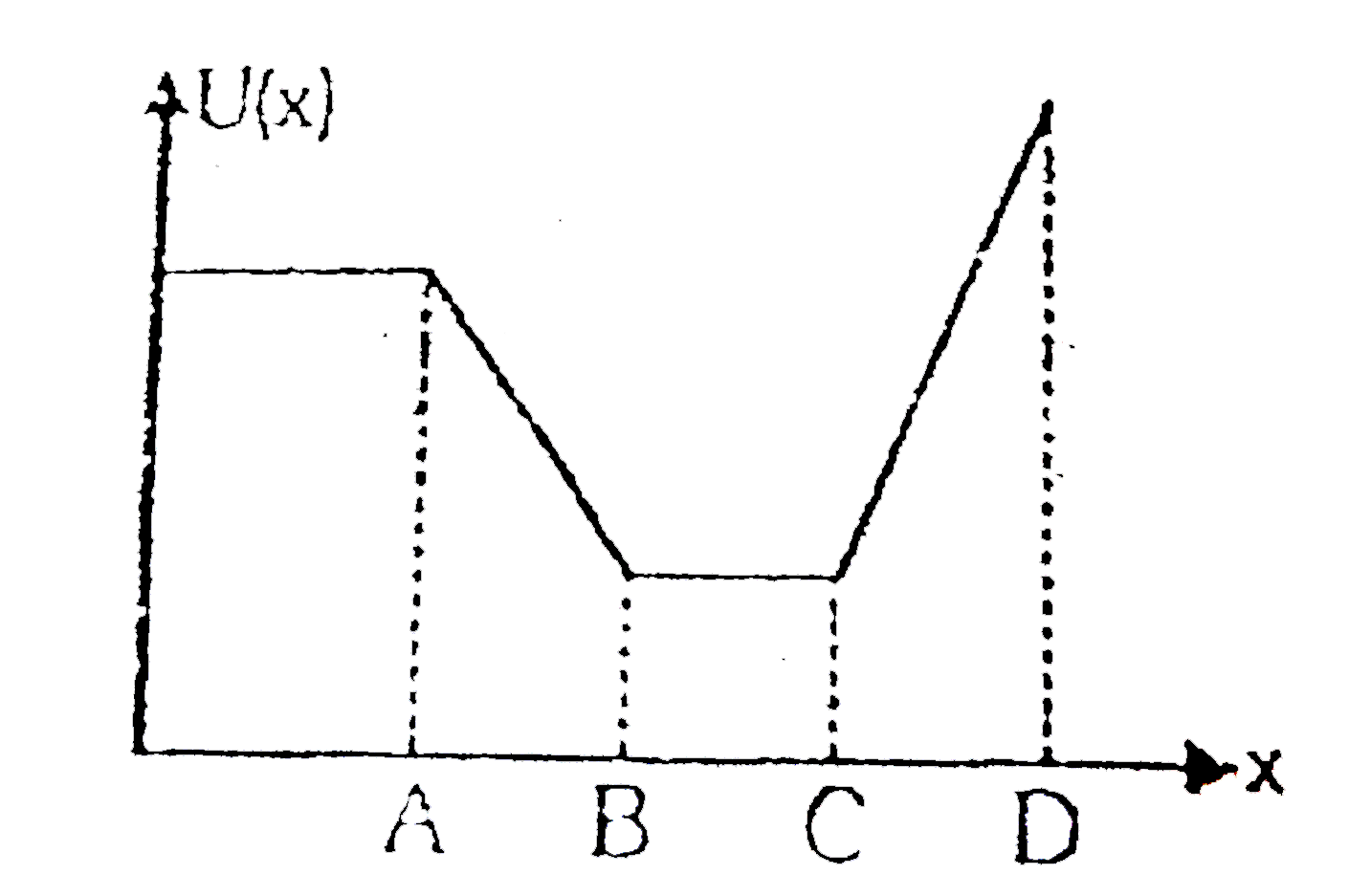
AB, BC, CD
AB, CD, BC
BC, CD, AB
BC, AB, CD
The correct Answer is:D
−dUdx−F
Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
- TEST PAPER 1Book:ALLENChapter:TEST PAPER 1Exercise:PHYSICS
Explore 11 Videos
Similar Questions
A particle slides on frictionless x - y plane. It is acted on by a conservative force described by the potential - energy function U(x,y)=12k(x2+y2). Derive an expression for the force acting on the particle.
View SolutionFigure (A) shows potential energy as a function of x for a particle that is moving in the x-direction under a coriservative force.
Figure (B) shows potential energy as a function of x for another particle that is moving in the x-direction under a conservative force.
Figure (C ) shows interaction potential energy as a system of two particles that could move in the x-direction under the mutual conservative force.
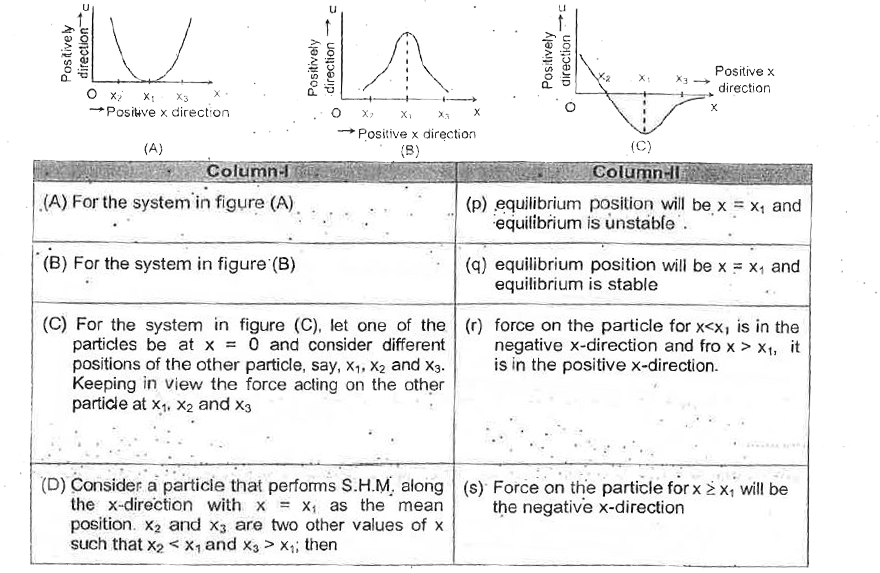
View Solution
Knowledge Check
A particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.
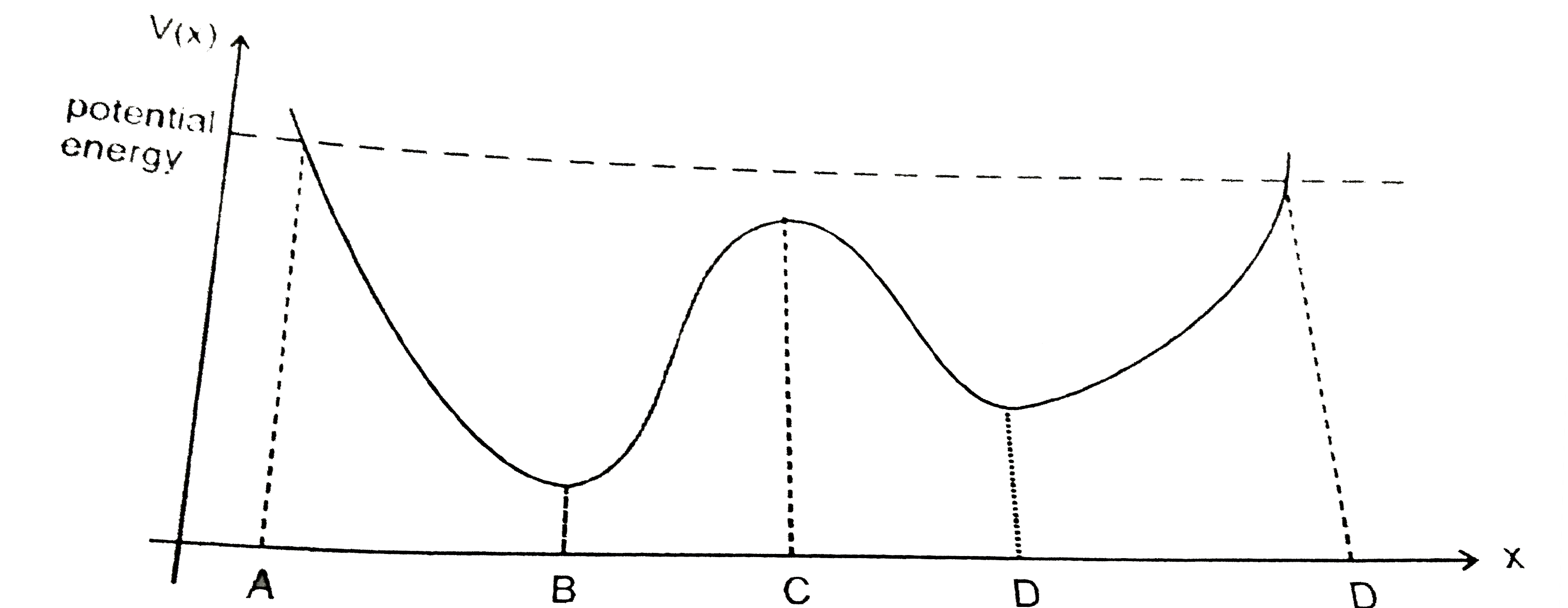
If the particle starts to move from rest from the point A, thenAthe speed is zero at the point A and E.Bthe acceleration vanished at the point A,B,D,C,ECthe acceleration vanished at the points B,C,DDthe speed is maximum at the point D.A particle is to move along the x−axis from x=0 to x=x1 while a conservative force, directed along the x−axis, acts on the particle. For each force defination presented in the figures the maximum magnitude of the force (F1) is the same for all cases. Rank the forces according to the change in potential energy associated with the motion shown. from most positive to most negative:
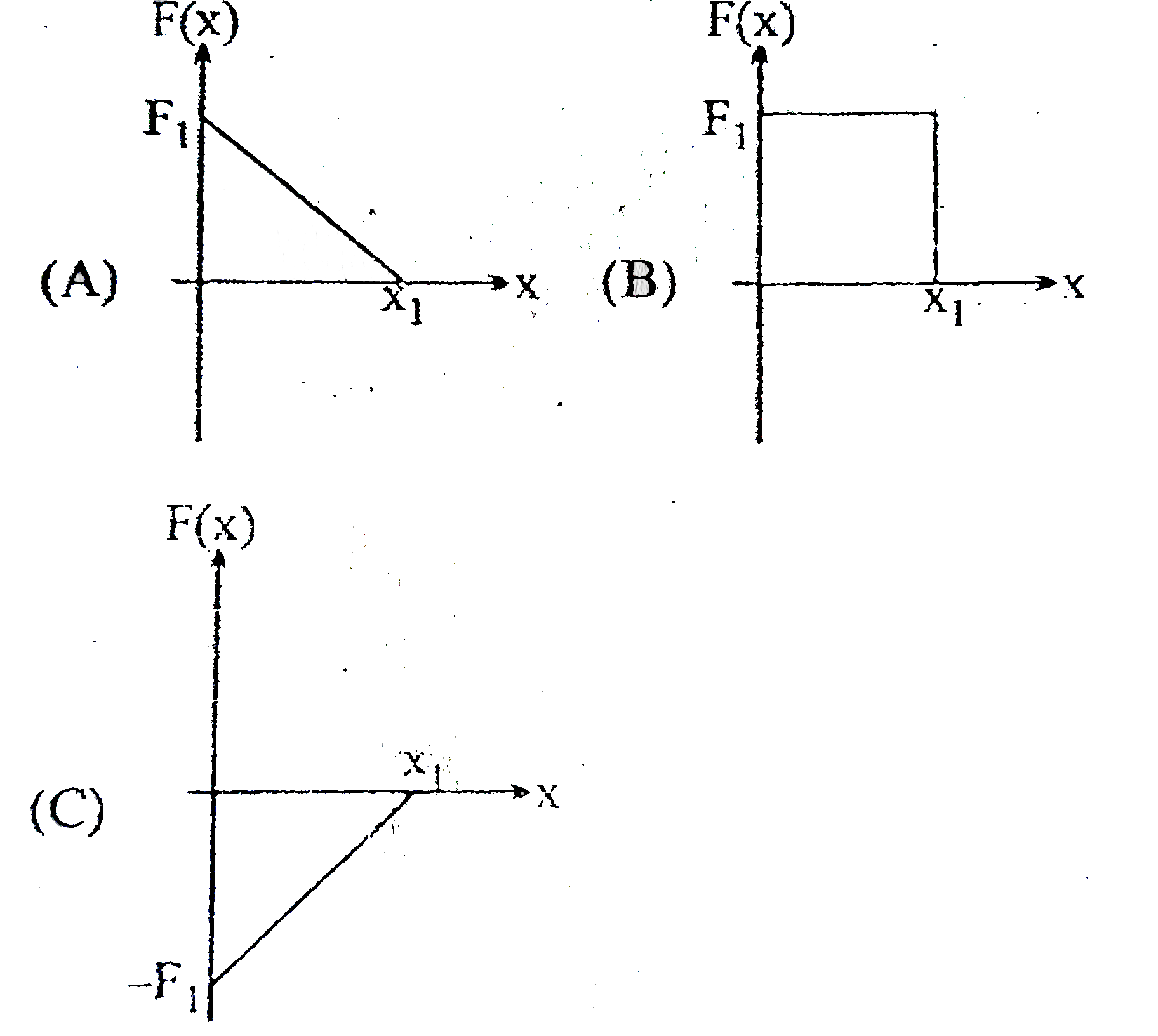 AC,A,BBB,A,CCC,B,ADA,B,C
AC,A,BBB,A,CCC,B,ADA,B,CA particle is moving along x-axis. Its x-coordinate versus time graph is as shown below.
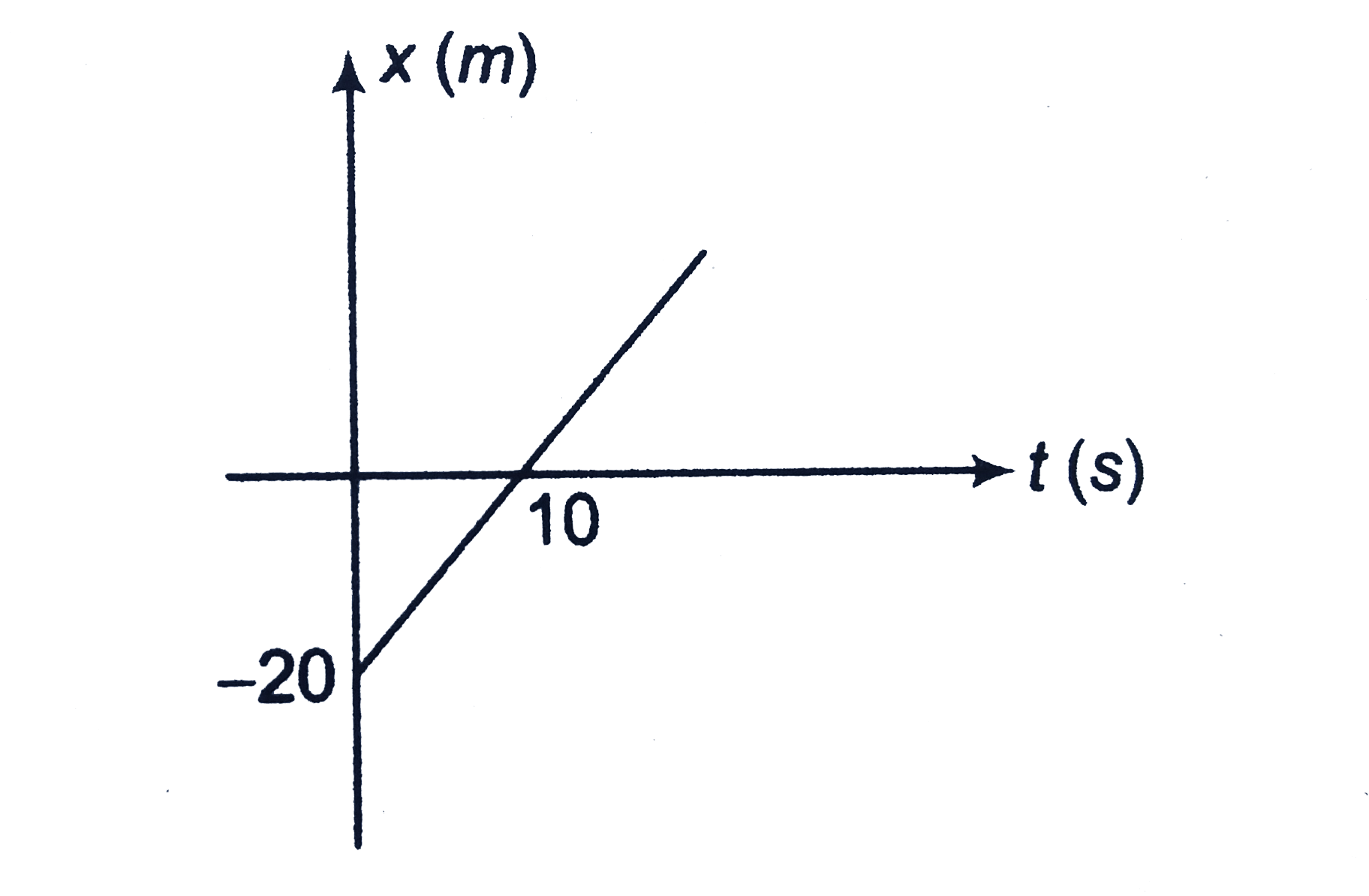 Draw some conclusion from the given graph. A+2msB+1msC+12msD+20ms
Draw some conclusion from the given graph. A+2msB+1msC+12msD+20ms
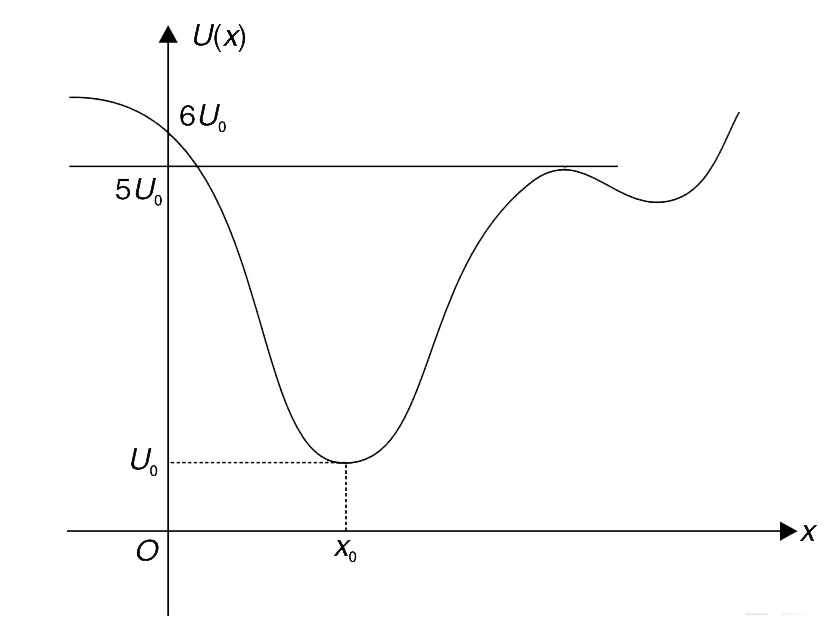
A particle is constrained to move along x axis under the action of a conservative force. The potential energy of the particle varies with position x as shown in the figure. When the particle is at x = x0, it is given a kinetic energy (k) such that 0 lt k lt 4U0 (a) Does the particle ever reach the origin? (b) Qualitatively describe the motion of the particle
View SolutionA paticle is acted upon by a force of constant magnitude which always remains perpendicular to the velocity of the particle. If that particle moves in a horizontal plane, then
View SolutionA 2.00 kg particle moves along an x axis in onedimensional motion while a conservative force along that axis acts on it. The potential energy U(x) associated with the force is plotted in Fig. 8-36a. That is, if the particle were placed at any position between x=0 and x=7.00m, it would have the plotted value of U. At x=6.5m, the particle has velocity →v0=(−4.00m/s)ˆi.
(c) Evaluate the force acting on the particle when it is in the region 1.9 m<x<4.0 m.
View SolutionA particle is moving on frictionless XY-plane. It is acted on by a conservative force described by the potential-energy function.
U(x,y,z)=12k(x2+y2+z2)
where , k=constant
Derive an expression for the force an the particle.
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

View Solution

