cylindrical volume of radius R has a uniform axial magnetic field B, which is increasing at a rate of . A chord (AB) of the circular cross section of the cylindrical region has length L.Calculate the line integral of induced electric field as one moves along the chord from A to B. Try to find the answer without actually performing the integration. Is the value of integral same if one moves along the arc from A to B ?

The correct Answer is:
Step by step video, text & image solution for cylindrical volume of radius R has a uniform axial magnetic field B, which is increasing at a rate of (dB)/(Dt) = alpha Ts^(-1). A chord (AB) of the circular cross section of the cylindrical region has length L.Calculate the line integral of induced electric field (int_(A)^(B) vec(E) vec(dl)) as one moves along the chord from A to B. Try to find the answer without actually performing the integration. Is the value of integral same if one moves along the arc from A to B ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:ARIHANTChapter:ELECTROMAGNETIC INDUCTIONExercise:Level 3
Explore 12 Videos
- ELECTROMAGNETIC INDUCTIONBook:ARIHANTChapter:ELECTROMAGNETIC INDUCTIONExercise:Level 3
Explore 12 Videos
- CURRENT ELECTRICITYBook:ARIHANTChapter:CURRENT ELECTRICITYExercise:Current Electricity
Explore 105 Videos
- ELECTROSTATICSBook:ARIHANTChapter:ELECTROSTATICSExercise:Level 3
Explore 59 Videos
Similar Questions
A uniform magnetic field →B fills a cylindrical volumes of radius R. A metal rod CD of length l is placed inside the cylinder along a chord of the circular cross-section as shown in the figure. If the magnitude of magnetic field increases in the direction of field at a constant rate dB/dt, find the magnetitude and direction of the EMF induced in the rod.

View SolutionConsider a cylindrical surface of radius R and length l in a uniform electric field E. Compute the electric flux if the axis of the cylinder is parallel to the field direction.
View Solution
Knowledge Check
Metal ring of radius R is placed perpendicular to uniform magnetic field B. Magnetic field starts changing at a rate α
AElectric field at any point on the ring is zero.BElectric field at any point on the ring is α(R)/(2)CEmf induced in the ring is zeroDEmf induced in the ring is πaR2An electron is moving in a circle of radius 'r' in a uniform magnetic field 'B'. Suddenly the field is reduced to 'B'2. The radius of the circular path now becomes
Ar2B2rCr4D4rA very long cylindrical wire is carrying a current I0 distriuted uniformly over its cross-section area. O is the centre of the cross-section of the wire and the direction of current in into the plane of the figure. The value ∫BA→B.→dl along the path AB (from A to B ) is
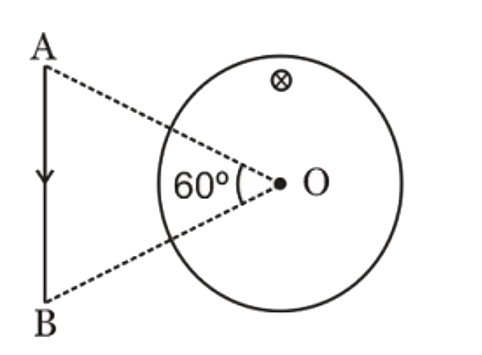 Aμ0I0B−μ0I06Cμ0I06Dμ0I03
Aμ0I0B−μ0I06Cμ0I06Dμ0I03
A conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA cylindrical space of radius R is filled with a uniform magnetic induction parallel to the axis of the cylinder. If B charges at a constant rate, the graph showin the variation of induced electric field with distance r from the axis of cylinder is
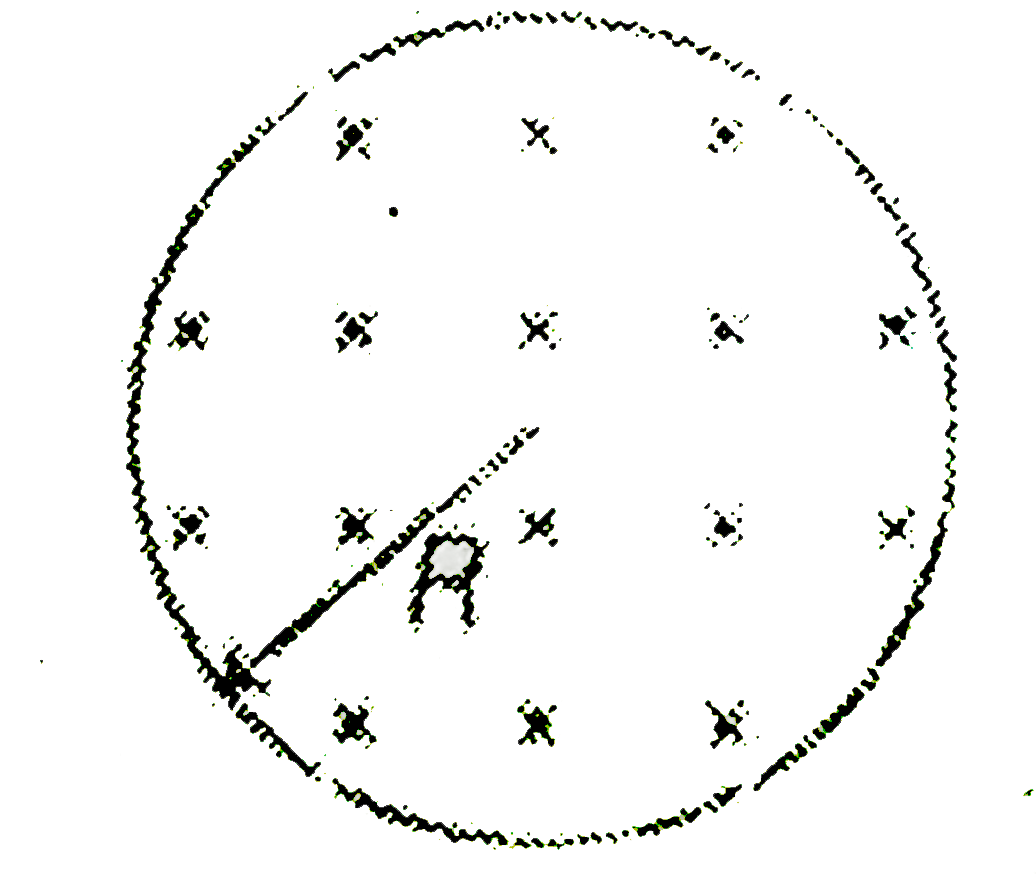
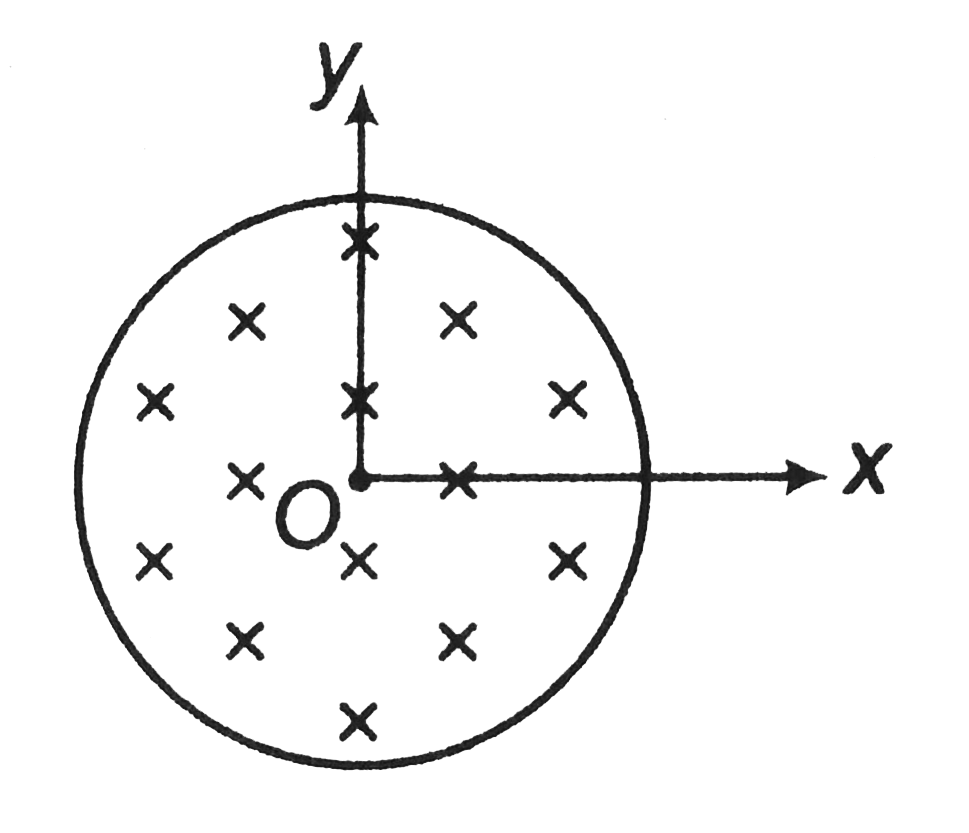
View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
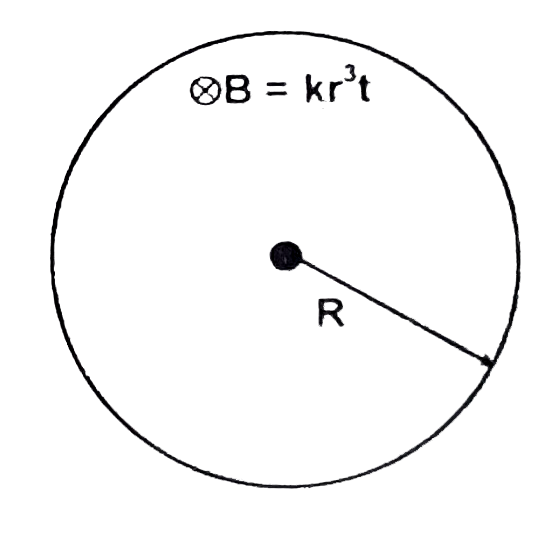
View SolutionA time varying magnetic field B=Kr3t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at rR2 is
View SolutionA: The electric field induced due to changing magnetic field is non-conservative,
R: The line integral of the electric field induced due to changing magnetic field along a closed loop is always zero.
View Solution

