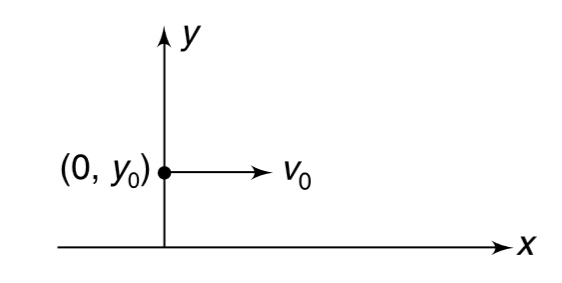
Electric field in xy plane is directed along positive y direction and

A particle of charge per unit mass $α$ is released from origin with a velocity $\to v = v_{0} ˆ i$ uniform magnetic field $\to B = - B_{0} ˆ k$ . If the particle passes through $(0, y, 0)$ , then $y$ is equal to
A $- \frac{2 v_{0}}{B_{0} α}$
B $\frac{v_{0}}{B_{0} α}$
C $\frac{2 v_{0}}{B_{0} α}$
D $- \frac{v_{0}}{B_{0} α}$
A uniform electric field $E_{0}$ is directed along positive y-driection. Find the change in electric potential energy of a positive test charge $q_{0}$ when it is displaced in this field from $y_{i} = a$ to $y_{f} = 2 a$ along the y-axis.
A $- q_{0} E_{0} a$
B $q_{0} E_{0} a$
C $\frac{- q_{0} E_{0}}{a}$
D $\frac{q_{0} E_{0}}{a}$
A charged particle of mass m and charge q is released from rest the position $(x_{0}, 0)$ in a uniform electric field $E_{0} ˆ j$ . The angular momentum of the particle about origin.
Ais zero
Bis constant
Cincreases with time
Ddecreases with time

The correct Answer is: $s q q r t (\frac{2 q a}{3 m V_{0}^{2}} (y^{3} - y_{0}^{2}))$