(i) A sinusoidal wave is travelling along positive x direction and the displacements at two positions x=0 and x=1m are given by y(0,t)=0.2cos(3πt) and y(1,t)=0.2cos(3πt+π8) Find all possible wavelength of the wave if it is known that wavelength is greater than 0.4 m.
(ii) A transverse sine wave of amplitude a=0.1cm is travelling along a string laid along the x-axis. The displacement (y) – time (t) graph of the string particle at x=0.1m is shown in first figure. The shape of the string at time t=0.1s is shown in second figure. At this time the particle at x=0.11m is having velocity in positive y direction write the equation of wave.

The correct Answer is:(i) 1615m and 1631m
(ii) y=(0.1cm)cos[(20πm−1x]+(10πs−1)t]
Step by step video, text & image solution for (i) A sinusoidal wave is travelling along positive x direction and the displacements at two positions x = 0 and x = 1 m are given by y (0, t) = 0.2 cos (3 pi t) and y(1, t)=0.2 cos (3pit+pi/8) Find all possible wavelength of the wave if it is known that wavelength is greater than 0.4 m. (ii) A transverse sine wave of amplitude a = 0.1 cm is travelling along a string laid along the x-axis. The displacement (y) – time (t) graph of the string particle at x = 0.1 m is shown in first figure. The shape of the string at time t = 0.1 s is shown in second figure. At this time the particle at x = 0.11 m is having velocity in positive y direction write the equation of wave. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A wave pulse is travelling on a string at 2m/s along positive x-directrion. Displacement y of the particle at x = 0 at any time t is given by
y=2t2+1 Find
Shape of the pulse at t = 0 and t = 1s.
View SolutionA sinusoidal wave having wavelength of 6m propagates along positive x direction on a string. The displacement (y) of a particle at x=2m varies with time (t) as shown in the graph
(a) Write the equation of the wave
(b) Draw y versus x graph for the wave at t=0

View Solution
Knowledge Check
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
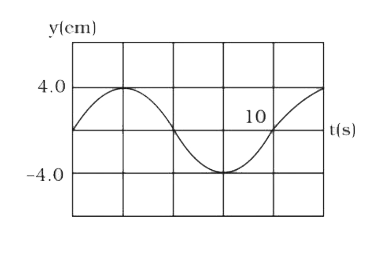
Q. Skecth of one wavelength of the wave (the portion between x=0 and x=20cm) at time t=0 is:A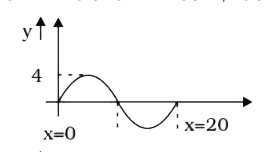 B
B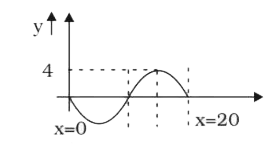 C
C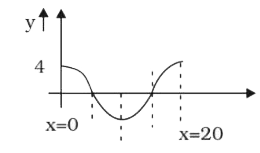 D
D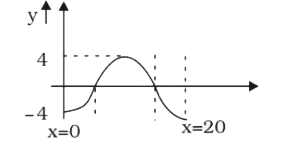
A wave travelling in the +ve x-direction having displacement along y-direction as 1m, wavelength 2π m and frequency of 1/π Hz is represented by
Ay=sin(2πx−2πt)By=sin(10πx−20πt)Cy=sin(2πx+2πtDy=sin(x−2t)A transverse wave, whose amplitude is 0.5 m wavelength is 1 m and frequency is 2Hz. is travelling along positive x direction. The equation of this wave will be-
Ay=0.5cos(2πx−4πt)By=0.5cos(2πx−4πt)Cy=0.5sin(πx−2πt)Dy=0.5cos(2πx−2πt)
A sinusoidal wave trsvelling in the positive direction on a stretched string has amplitude 2.0cm, wavelength 1.0cm and velocity 5.0m/s. At x=0 and t=0 it is given that y=0 and ∂y∂t<0. Find the wave function y(x,t).
View SolutionA transverse wave of wavelength 50 cm is travelling towards+vex-axis along a string whose linear density is 0.05g/cm. The tension in the string is 450 N. At t=0,the particle at x=0 is passing through its mean position wave. The amplitude of the wave is 2.5 cm.
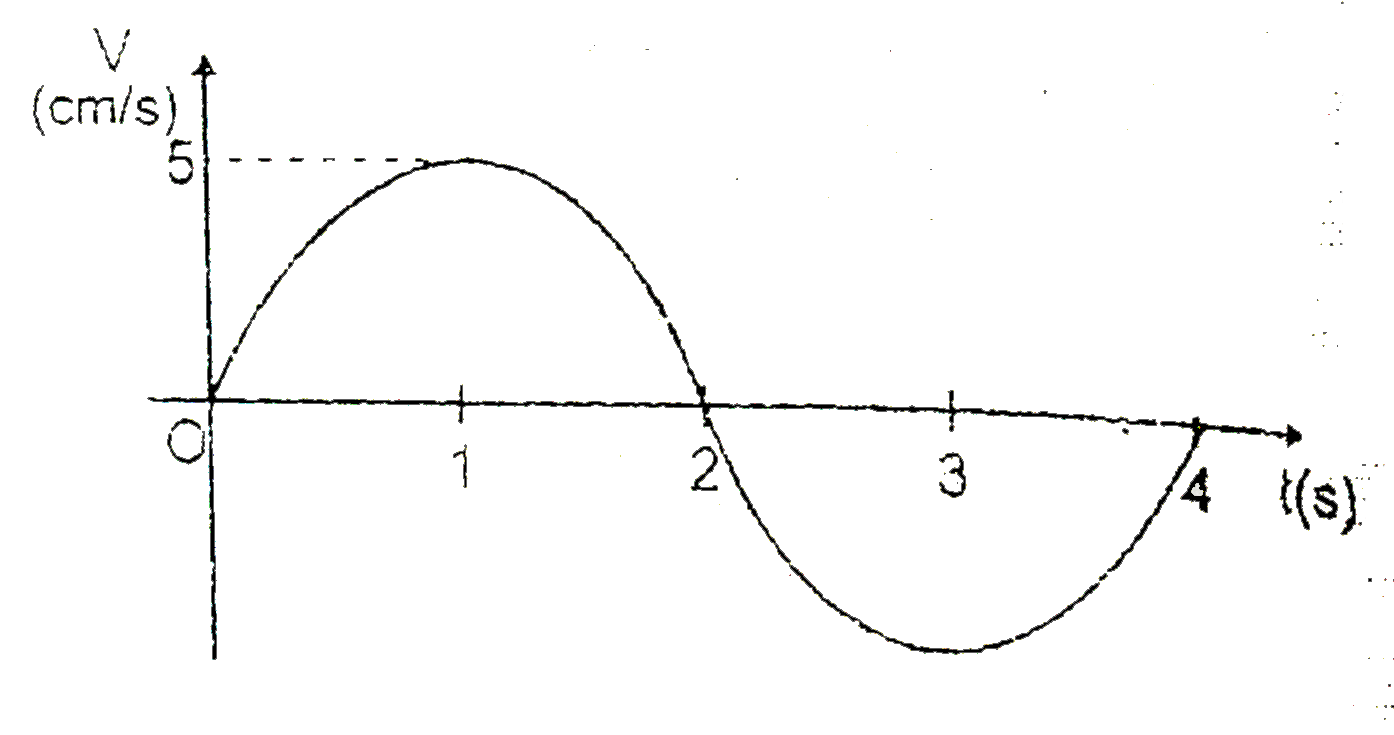
View SolutionA certain transvers sinusoidal wave of wavelength 20cm is moving in the positive X direction. The transverse velocitt of the particle at x=0 as a function of time is shonwn. The amplitude of the motion is equal to xπ (in cm). Find x :
View SolutionTwo sinusoidal waves travelling in opposite directions interfere to produce a standing wave described by the equation
y=(1.5m)sin(0.400x)cos(200t)
where, x is in meters and t is in seconds. Determine the wavelength, frequency and speed of the interfering waves.
View SolutionA standing wave is formed by the superposition of two waves travelling in the opposite directions. The transverse displacement is given by
y(x,t)=0.5sin(5π4x)cos(200πt)
What is the speed of the travelling wave moving in the postive X direction ?
View Solution

