A transverse wave of wavelength 50 cm is travelling towards+vex-axis along a string whose linear density is 0.05g/cm. The tension in the string is 450 N. At t=0,the particle at x=0 is passing through its mean position wave. The amplitude of the wave is 2.5 cm.
Let the wave be described by:
yx,tAsinωx−ωtϕ0ωandA=2.5cm
where k=2πλ=2π0.5=4π
y(0,0)=0⇒Asinϕ0=0
ϕ00,π
we also have
(dydt)0.0<0⇒−Aωcosϕ0>0
From Eqs.(i) and (ii), we get ϕ0π
Velocity of transverse wave in the string is given by
√Tμ=√4500.05×10−1=300m/s
⇒ω=2πf=2πcλ=π(300)0.5=1200πrad/s
using all the quntities, the equation is
y2.5sin4πx−1200πtπcm
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Example
9 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.1
9 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
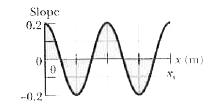
A sinusoidal wave travels along a string under tension. Figure 16-52 gives the slopes along the string at time t=0. The scale of the x axis is st by xs=0.40m What is the amplitude of the wave?
View Solution(i) A sinusoidal wave is travelling along positive x direction and the displacements at two positions x=0 and x=1m are given by y(0,t)=0.2cos(3πt) and y(1,t)=0.2cos(3πt+π8) Find all possible wavelength of the wave if it is known that wavelength is greater than 0.4 m.
(ii) A transverse sine wave of amplitude a=0.1cm is travelling along a string laid along the x-axis. The displacement (y) – time (t) graph of the string particle at x=0.1m is shown in first figure. The shape of the string at time t=0.1s is shown in second figure. At this time the particle at x=0.11m is having velocity in positive y direction write the equation of wave.

View Solution
Knowledge Check
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
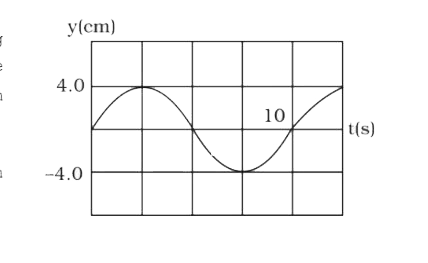
Q. The transverse velocity of the particle at x=0 at t=5.0 s is ?A−2cm/sB+2cm/sC+1.5cm/sD−2.5cm/sA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
Q. Skecth of one wavelength of the wave (the portion between x=0 and x=20cm) at time t=0 is:A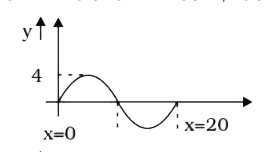 B
B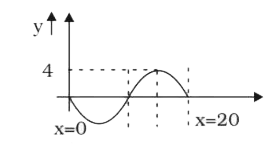 C
C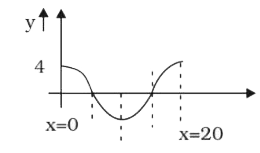 D
D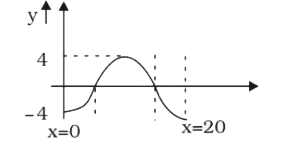
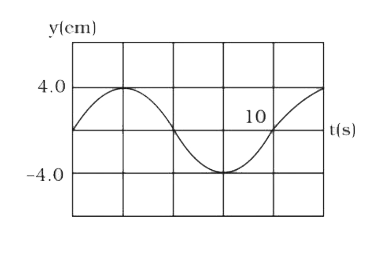
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
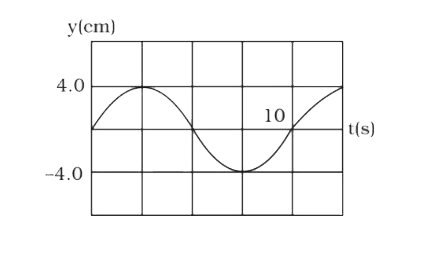
Q. The velocity of propagation of the wave is ?A2cm/sB4cm/sC1cm/sD8cm/s
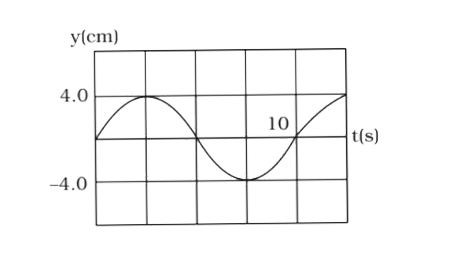
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
View SolutionA transverse wave described by y=0.5sin(x+40t) is propagating on a vibrating string of linear density 0.01 kg/m. If x and y are in metre and time is in second, then the tension in the wire is
View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is
View SolutionThe tension in a string with a linear density of 0.0010 kg/m iş 0.40 N. A 100 Hz sinusoidal wave on this string has a wavelength of
View Solution
