A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
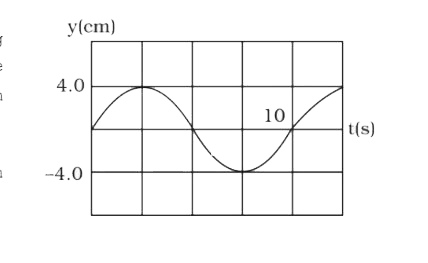
Q. The transverse velocity of the particle at x=0 at t=5.0 s is ?
−2cm/s
+2cm/s
+1.5cm/s
−2.5cm/s
The correct Answer is:D
Wave equation,
y=Asin(kx−ωt+ϕ)=4sin[2π20x−2π×0.1t+ϕ]
At t=0, x=0, y=0
⇒ϕ=0 or π
But at position x=0 as time progresses, particle starts moving along positive y-direction
∴ϕ=π satisfies
∴Equationn of wave will be y=4sin(π10x−0.2πt+π), x in cm and t is sec.
∴Particle-velocity
vp(x,y)=δyδt=4cos(π10x−0.2πt+π)×(0.2π)
∴vp(0,5)=4cos(π10×0−0.2π×5+π)×(−0.2π)=−0.8π=−2.5cm/s
Similar Questions
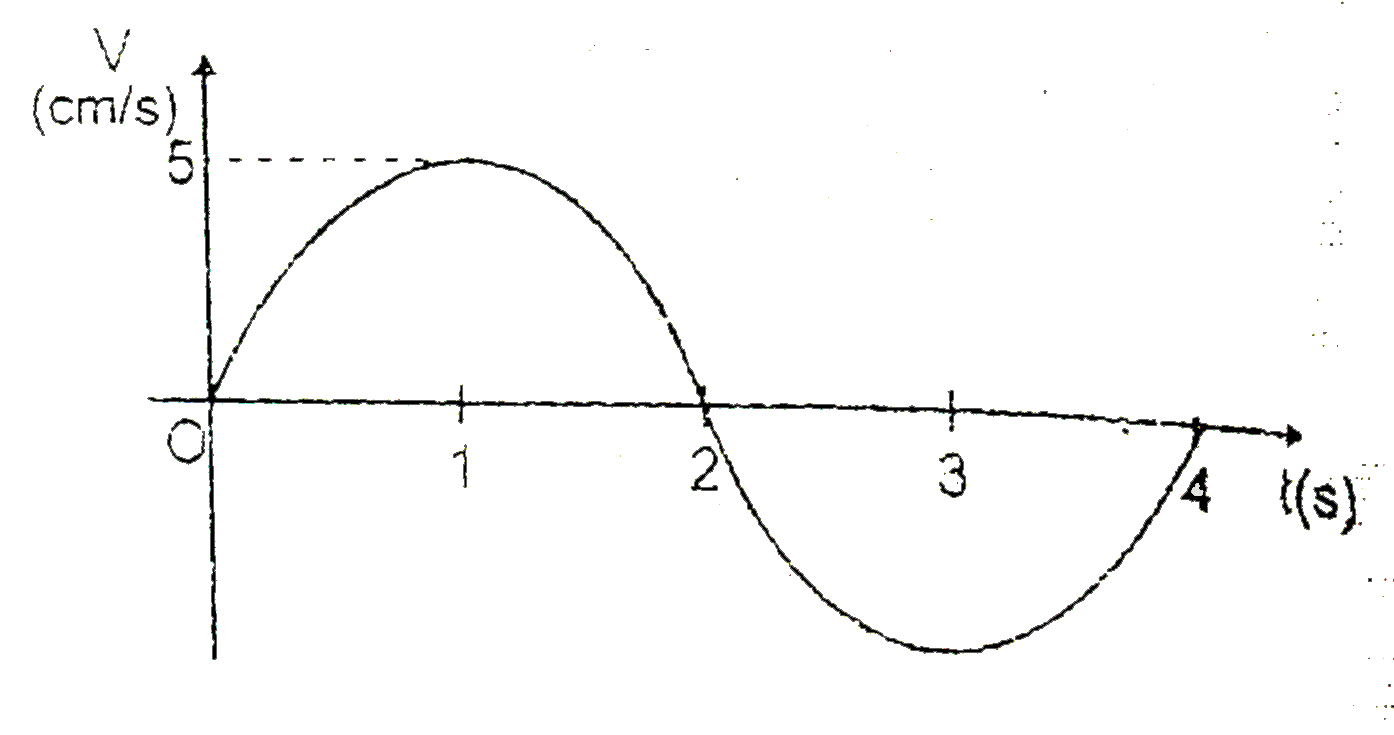
A certain transvers sinusoidal wave of wavelength 20cm is moving in the positive X direction. The transverse velocitt of the particle at x=0 as a function of time is shonwn. The amplitude of the motion is equal to xπ (in cm). Find x :
View Solution(i) A sinusoidal wave is travelling along positive x direction and the displacements at two positions x=0 and x=1m are given by y(0,t)=0.2cos(3πt) and y(1,t)=0.2cos(3πt+π8) Find all possible wavelength of the wave if it is known that wavelength is greater than 0.4 m.
(ii) A transverse sine wave of amplitude a=0.1cm is travelling along a string laid along the x-axis. The displacement (y) – time (t) graph of the string particle at x=0.1m is shown in first figure. The shape of the string at time t=0.1s is shown in second figure. At this time the particle at x=0.11m is having velocity in positive y direction write the equation of wave.

View Solution
Knowledge Check
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.

Q. The velocity of propagation of the wave is ?A2cm/sB4cm/sC1cm/sD8cm/sA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
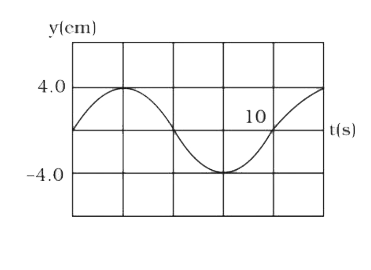
Q. Skecth of one wavelength of the wave (the portion between x=0 and x=20cm) at time t=0 is:A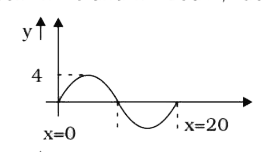 B
B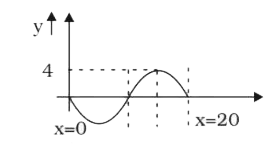 C
C D
D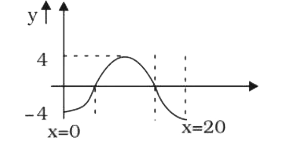
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
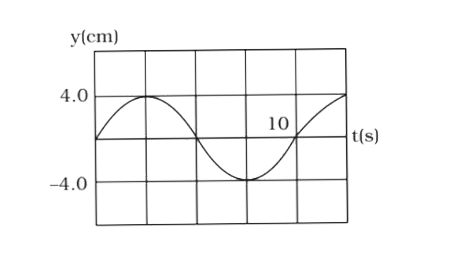 Ay=(4.0cm)sin(π10x−π5t),x in cm and t in sec.By=(4.0cm)sin(π10x+π5t),x in cm and t in secCy=(4.0cm)sin(π10x−π5t+π), x in cm and t in secDy=(4.0cm)cos(π10x−π5t+π),x in cm and t in sec
Ay=(4.0cm)sin(π10x−π5t),x in cm and t in sec.By=(4.0cm)sin(π10x+π5t),x in cm and t in secCy=(4.0cm)sin(π10x−π5t+π), x in cm and t in secDy=(4.0cm)cos(π10x−π5t+π),x in cm and t in sec
A transverse sinusoidal wave is moving along a string in the opposite direction of an x axis with a speed of 70m/s. At t=0 the string particle at x=0 has a transverse displacement of 4.0 cm and is not moving. The maximum transverse speed of the string particle at x=0 is 16m/s. (a) What is the frequency of the wave? (b) What is the wavelength of the wave? If y(x,t) =ymsin(kx±ωt+ϕ) is the form of the wave equation, what are (c) ym,(d)k,(e)ω(f)ϕ, and (g) the correct of sign in front of ω?
View SolutionA sinusoidal transverse wave of wavelength 18 cm travels along a string in the positive direction of an x axis. The displacement y of the string particle at x= 0) is given in Fig. 16-41 as a function of time t. The scale of the vertical axis is set by y1=4.0cm, The wave equation is to be in the form y(x,t)=ynIsin(kx±ωt+ϕ). (a) At t= 0), is a plot of y versus x in the shape of a positive sine function on a legative sinc function? What are (b)ynI(c)k,(d)ω(e)ϕ, (f) the sign in front of ω, and (g) the speed of the wave? (h) What is the transverse velocity of the particle at x=0 when t=5.0 s?
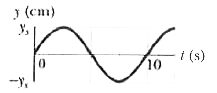
View SolutionA certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

View Solution
The velcocity displacement graph of a particle moving along a straight line is shown in figure. The velocity as function of x(0≤x≤1) is
View SolutionA pulse is started at a time t=0 along the +xdirection on a long, taut string. The shape of the pulse at t=0 is given by function f(x) with
here f and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N.
The transverse velocity of the particle at x=13cm and t=0.015s will be
View Solution

