A wave pulse is travelling on a string at $2 m / s$ along positive x-directrion. Displacement y of the particle at x = 0 at any time t is given by
$y = \frac{2}{t^{2} + 1}$ Find
Shape of the pulse at t = 0 and t = 1s.

Video Solution

Text Solution

Verified by Experts

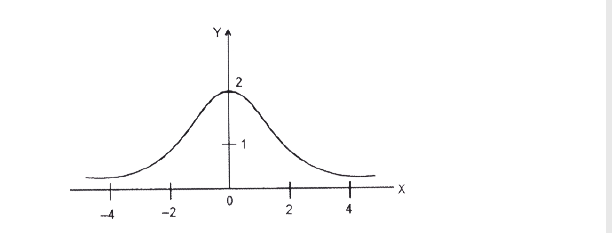
We can use wave function at a particular instant, say t = 0, to find shape of the wave pulse using different values of x.
at $t = 0 y = \frac{2}{\frac{x^{2}}{4} + 1}$
at $x = 0 y = 2$
$\begin{matrix} x = 2 & y = 1 x = - 2 & y = 1 x = 4 & y = 0.4 x = - 4 & y = 0.4 \end{matrix}$
Using these value, shape is drawn.
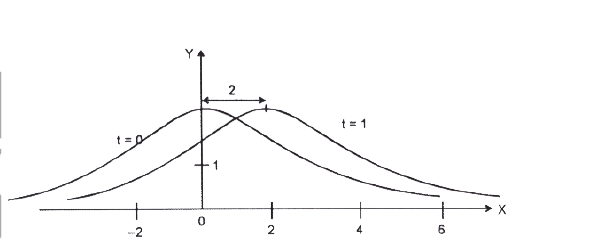
Similarly for t = 1 s shape can be drawn. What do you conclude about direction of motion of the wave from the graphs? Also check how much the pulse has moved in 1s time interval. This is equal to wave speed. Here is the procedure.
$y = \frac{2}{{(t - \frac{x}{2})}^{2} + 1} a t 1 = 1 s$
$\begin{matrix} a t & x = 2 & y = 2 (maximum value) a t & x = 0 & y = 1 a t & x = 4 & y = 1 \end{matrix}$
The pulse has moved to the right by 2 units in 1st interval

Updated on:21/07/2023

If wave y = A cos $(ω t + k x)$ is moving along x-axis The shape of pulse at t = 0 and t = 2 s
Aare different
Bare same
Cmay not be same
DNone of these
A particle moves along a straight line such that its displacement at any time t is given by $s = 3 t^{3} + 7 t^{2} + 14 t + 5$ . The acceleration of the particle at $t = 1 s$ is
A $18 m / s^{2}$
B $32 m / s^{2}$
C $29 m / s^{2}$
D $24 m / s^{2}$
A pulse travelling at a speed of $2 \frac{m}{s}$ along the positive Z-axis is given by y $= \frac{3}{z^{2} + 1}$ at t= 0 .The wave function representing the pulse at any times is given by
A $y = \frac{3}{{(z - 2 t)}^{2} + 1}$
B $y = \frac{3}{{(z + 2 t)}^{2} + 1}$
C $y = \frac{3}{{(2 z + t)}^{2} + 1}$
D $y = \frac{3}{{(2 z - t)}^{2} + 1}$