Doubtnut Promotions Sticky

(i) There is a vertical loop of radius R. A small block of mass m is slowly pushed along the loop from bottom to a point at height h. Find the work done by the external agent if the coefficient of friction is mu. Assume that the external agent pushes tangentially along the path. (ii) A block of mass m slides down a smooth slope of height h, starting from rest. The lower part of the track is horizontal. In the beginning the block has potential energy U = mgh which gets converted into kinetic energy at the bottom. The velocity at bottom is v=sqrt(2gh). Now assume that an observer moving horizontally with velocity v=sqrt(2gh) towards right observes the sliding block. She finds that initial energy of the block is E=mgh+1/2 mv^(2) and the final energy of the block when it reaches the bottom of the track is zero. Where did the energy disappear?
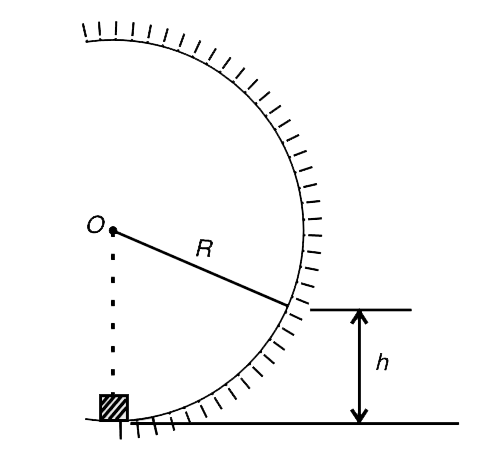
(i) There is a vertical loop of radius R. A small block of mass m is slowly pushed along the loop from bottom to a point at height h. Find the work done by the external agent if the coefficient of friction is μ. Assume that the external agent pushes tangentially along the path. (ii) A block of mass m slides down a smooth slope of height h, starting from rest. The lower part of the track is horizontal. In the beginning the block has potential energy U = mgh which gets converted into kinetic energy at the bottom. The velocity at bottom is v=√2gh. Now assume that an observer moving horizontally with velocity v=√2gh towards right observes the sliding block. She finds that initial energy of the block is E=mgh+12mv2 and the final energy of the block when it reaches the bottom of the track is zero. Where did the energy disappear?
ocr_image

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:(i)mgh+μmg√2Rh−h2

|
Answer

Step by step video, text & image solution for (i) There is a vertical loop of radius R. A small block of mass m is slowly pushed along the loop from bottom to a point at height h. Find the work done by the external agent if the coefficient of friction is mu. Assume that the external agent pushes tangentially along the path. (ii) A block of mass m slides down a smooth slope of height h, starting from rest. The lower part of the track is horizontal. In the beginning the block has potential energy U = mgh which gets converted into kinetic energy at the bottom. The velocity at bottom is v=sqrt(2gh). Now assume that an observer moving horizontally with velocity v=sqrt(2gh) towards right observes the sliding block. She finds that initial energy of the block is E=mgh+1/2 mv^(2) and the final energy of the block when it reaches the bottom of the track is zero. Where did the energy disappear? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023
Class 11PHYSICSWORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One or More

    A small mass m is moved slowly from the surface of the earth to a height h above the surface. The work done (by an external agent) in doing this is

    Amgh, for all values of h
    Bmgh, for h<<R
    C1/2 mgR for h=R
    D−1/2mgR for h=R
  • Question 2 - Select One

    A small mass m is moved slowly from the surface of the earth to a height h above the surface. The work done (by an external agent) in doing this is

    Amgh, for all values of h
    Bmgh, for h<<R
    C1/2,mgR, for h=R
    D−1/2mgR, for h=R
  • Question 3 - Select One or More

    A small mass m is moved slowly from the surface of the earth to a height h above the surface. The work done ( by an external agent) in doing this is

    Amgh, for all values of h
    Bmgh, for h<<R
    C12mgR for h = R
    D−12mgR, for h = R