A ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.

The correct Answer is:6
mv2+mg(R−r)(1−cosθ)= constant
⇒2mvdvdt+mg(R−r)sinθdthηdt=0
since v=ω(R−r)=−dthηdt(R−r)
dvdt=−d2θdt2(R−r)
2mdthηdt(R−r)d2θdt2(R−r)+mg(R−r)sinθdthηdt=0
⇒d2θdt2=−>hη2(R−r) (for small θ,sinθ=0)
⇒T=2π√2(R−r)g
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PT-01
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Pt-02
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 107 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
Similar Questions
A solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

View SolutionA semi cylindrical shell with negligible thickness oscillates without slipping on a horizontal surface. The time period of small oscillations is R
View Solution
Knowledge Check
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.A solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?
AMR22BMR2C32MR2D2MR2A symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
Av/RBContinuously increasingCDependent on mass MDIndependent of radius (R)
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA small block oscillates back and forth on a smooth concave surface of radius R. Find the time period of small oscillation.

View SolutionA small block oscillates back and forth on as smooth concave surface of radius R figure. Find the time period of small oscillation.

View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
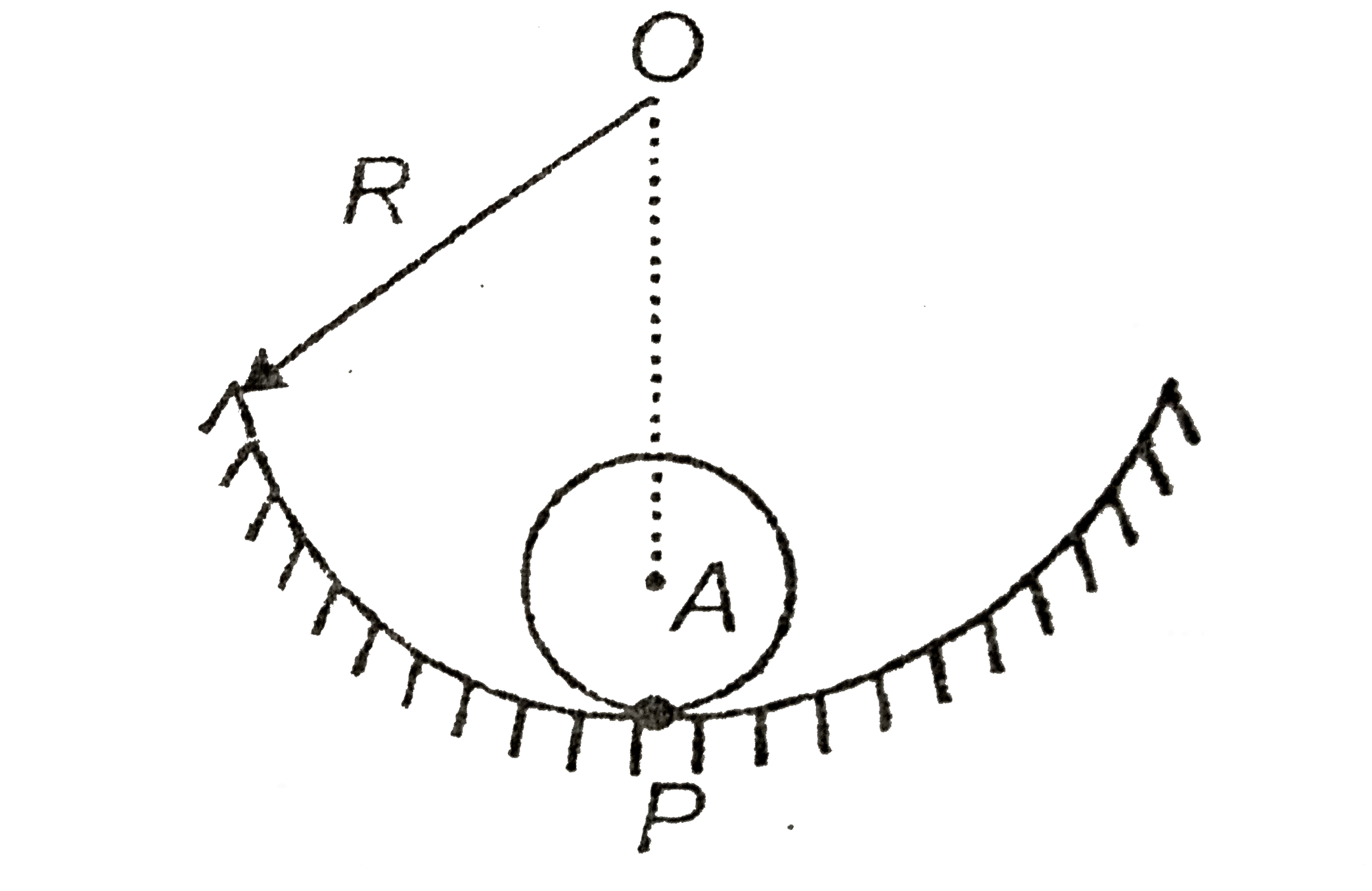
View SolutionA drum of radius R and mass M rolls down without slipping along an inclined plane of angle θ. The frictional force
View Solution