A hemisphere (radius R) is placed in electric field as shown in fig. Total outgoing flux is -

πR2E
2πR2E
4πR2E
(πR2E)/2
The correct Answer is:A
Step by step video, text & image solution for A hemisphere (radius R) is placed in electric field as shown in fig. Total outgoing flux is - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
A hemispherical bowl of radius r is placed in uniform electric field E . The electric flux passing through the bowl is
Aπr2EB2πrE2C4πr2ED4πrE2A hemispherical body of radius R is placed in a uniform electric field E. What is the flux linked with the curved surface if, the field is (a) parallel to the base, (b) perpendicular to the base.
Aϕ=(E(πR)Bϕ=(ES=E(πR3)Cϕ=E(πR2)Dϕ=(ES=E(πR4)A hemispherical body of radius R is placed in a uniform electric field E. If the field E is parallel to the base of the hemisphere the flux linked with it is
A2πREB2πR2ECπR2EDzero
A hemispherical body is placed in a uniform electric field E. What is the flux linked with the curved surface if the field is (a) parallel to base of the body , (b) perpendicular to base of the body and (c) perpendicular to the curved surface at every points as in figure.

View SolutionIf a hemispherical body is placed in a uniform electric field E then the flux linked with the curved surface is E B
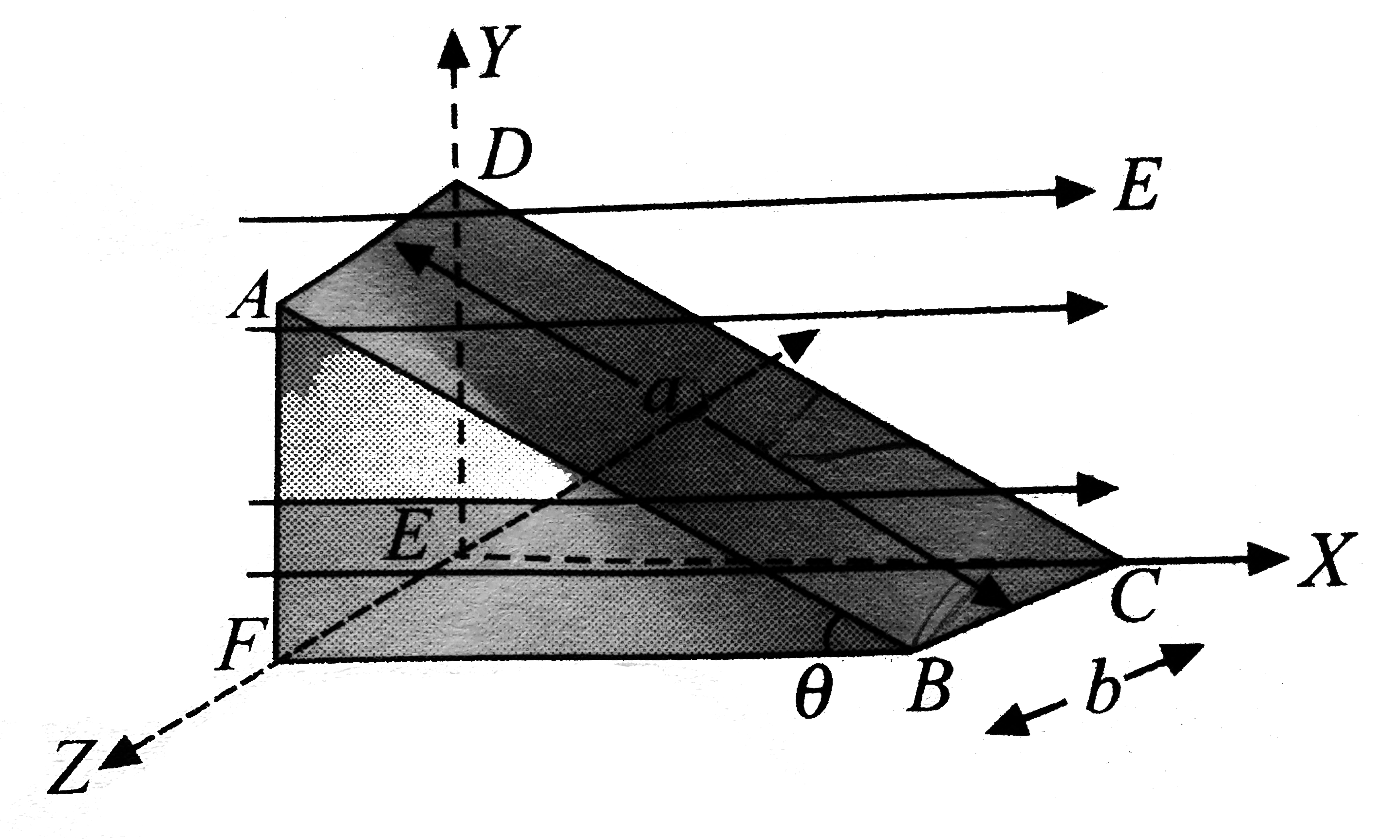
View SolutionA conic surface is placed in a uniform electric field E as shown in figure. Such that the field is perpendicular to the surface on the side AB. The base of the cone is of radius R, and the height of the cone is h. The angle of the cone is θ.

Find the magnitude of the flux that enters the cone's curved surface from the left side. Do not count the outgoing flux (θ<45∘).
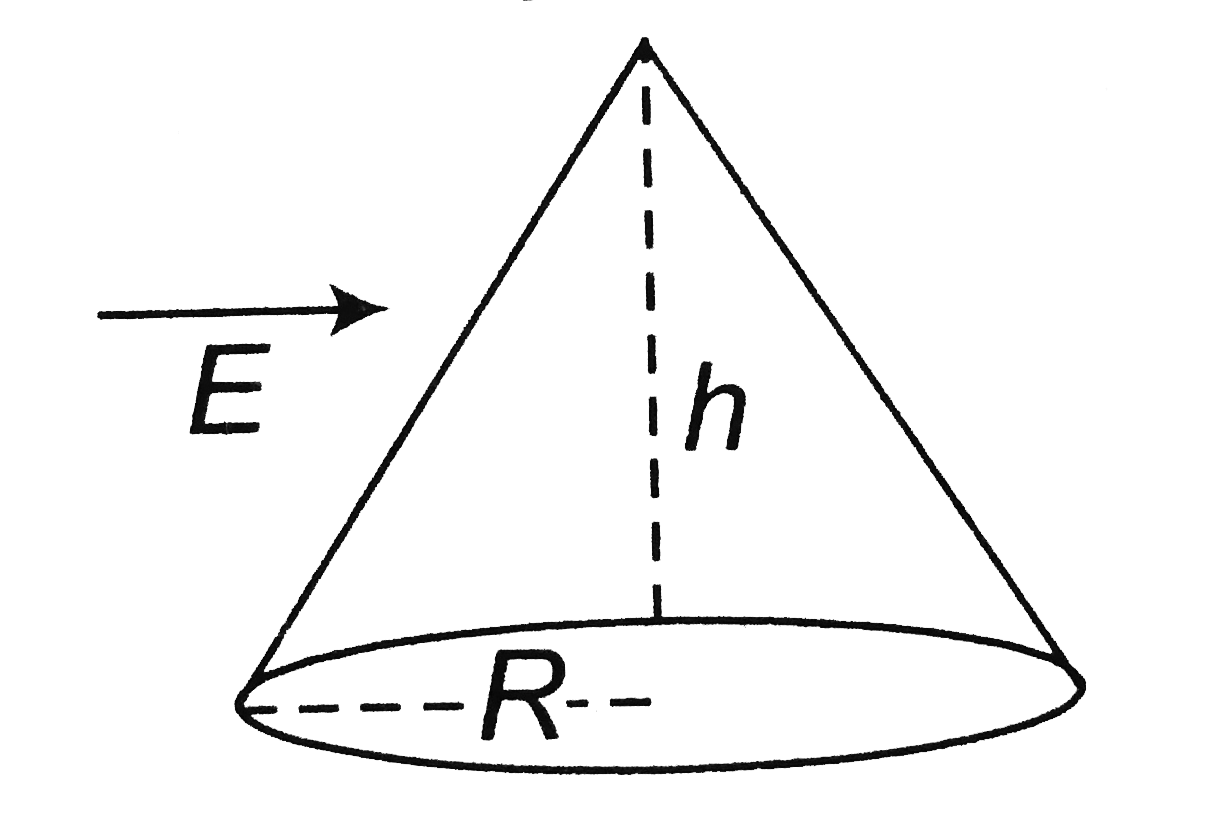
View SolutionA cone lies in a uniform electric field E as shown in figure. The electric flux entering the cone is
View SolutionThe electric flux through a hemispherical surface of radius R placed in a uniform electric field E parallel to the axis of the circular plane is
View Solution