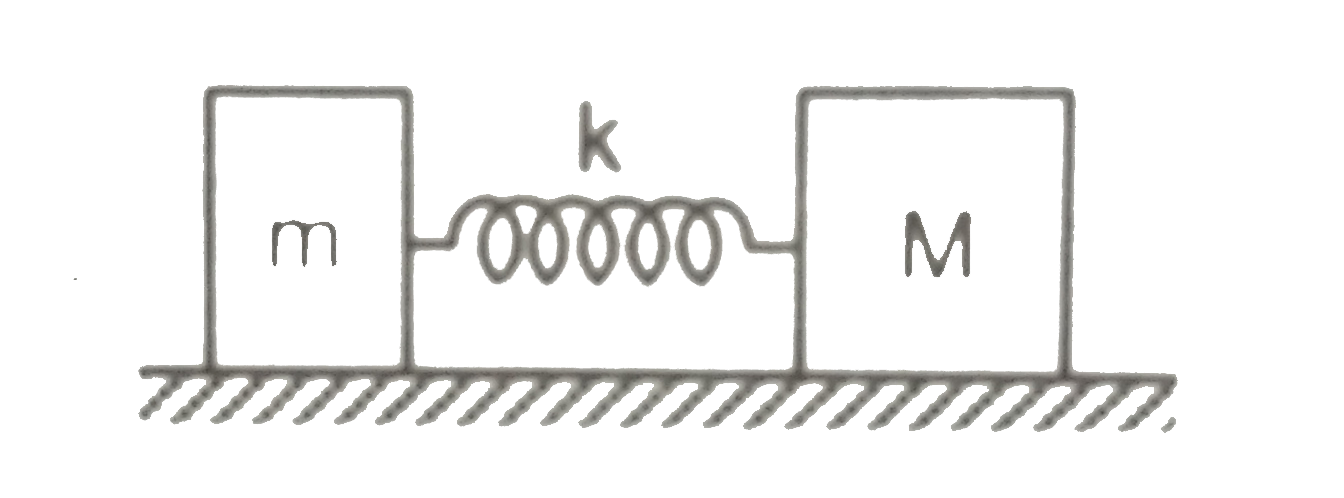
A light spring of spring constant k is kept compressed between two blocks of masses m and M on a smooth horizontal surface. When released, the blocks acquire velocities in opposite directions. The spring loses contact with the blocks when it acquires natural length. The spring was initially compressed through a distance, d. Find the final speed of the block of mass, m.
√kMm(M+m)×x
√kMm+(m+M)×x
√kMm(M−m)×x
√kMM(M−m)×x
The correct Answer is:A
Step by step video, text & image solution for A light spring of spring constant k is kept compressed between two blocks of masses m and M on a smooth horizontal surface. When released, the blocks acquire velocities in opposite directions. The spring loses contact with the blocks when it acquires natural length. The spring was initially compressed through a distance, d. Find the final speed of the block of mass, m. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
How much energy will be needed for a body of mass 100kg to escape from the earth- (G=10M/S2 and radius of earth = 6.4 xx 10^(6) m)
View SolutionA light spring of spring constant k is kept compressed between two blocks of masses m and M on a smooth horizontal surface. When released, the blocks acquire velocities in opposite directions. The spring loses contact with the blocks when it acquires natural length. I fhte spring was initially compressed through a distance d find the final speeds of the two blocks.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View SolutionA light spring of constant k is kept compressed between two blocks of masses m and M on a smooth horizontal surface. When released, the block acquire velocities in opposite directions. The spring loses contact with the blocks when it acquires natural length. if the spring was initially compressed through a distance x, find the final speeds of the two blocks.
View SolutionA block of mass m moving at a speed v_0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View SolutionA block of mass m is placed on a smooth block of mass M = m with the help of a spring as shown in the figure. A velocity v_(0) is given to upper block when spring is in natural length. Find maximum compression in the spring.
View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k'. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm'.
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force on the block of mass m.
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force on the block of mass m
View SolutionA light spring of spring constant k is kept compressed between two blocks of masses m and M on a smooth horizontal surface. When released, the blocks acquire velocities in opposite directions. The spring loses contact with the blocks when it acquires natural length. If the spring was initially compressed through a distance d find the final speeds of the two blocks.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially, the blocks are at rest and the spring is unstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstreatched. Then a constant force F starts acting on the block of mass M to pull it. Find the force on the block of mass m.
View Solution

