Question

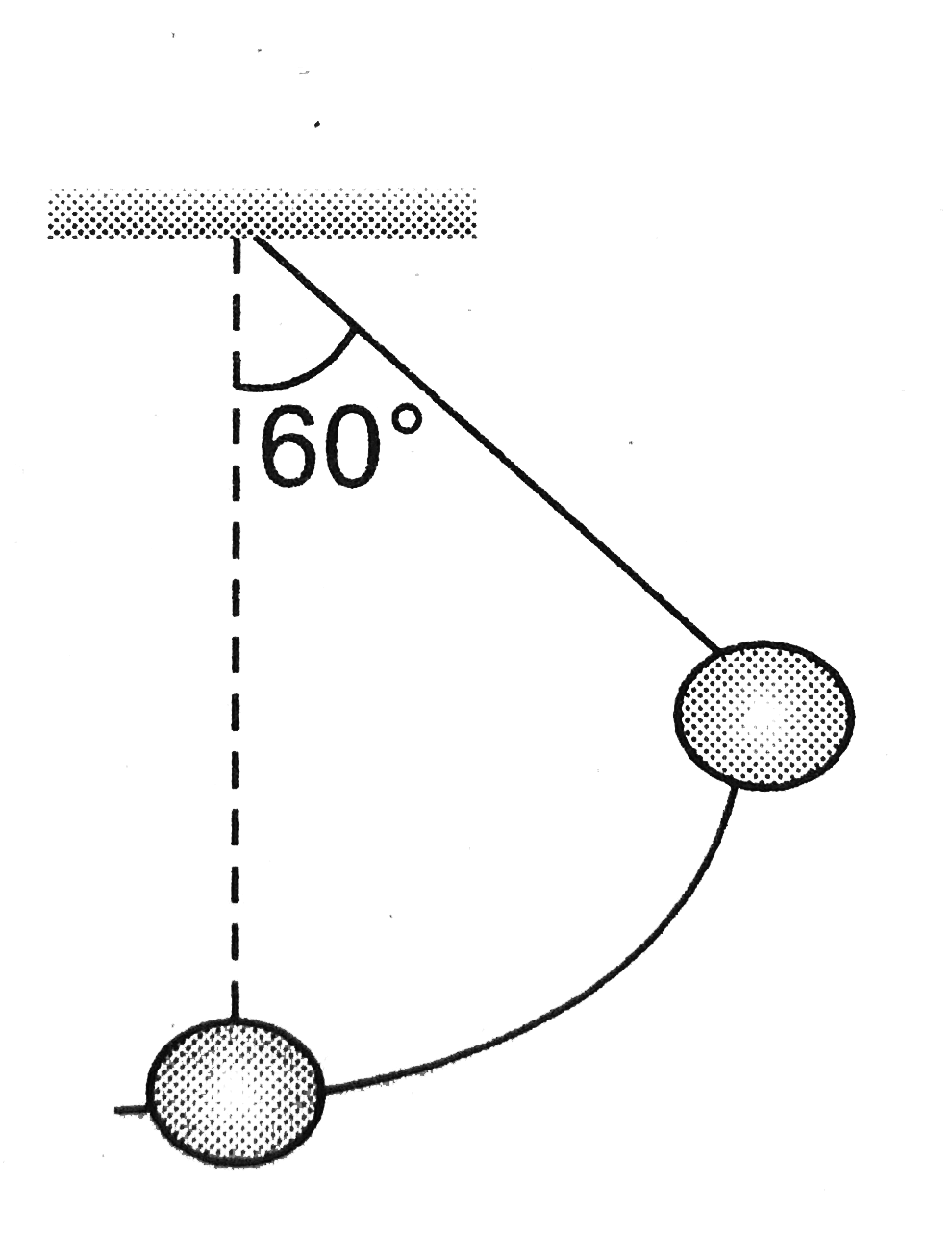
A pendulum of mass 1 kg and length  = 1m is released from rest at angle  = 60º. The power delivered by all the forces acting on the bob at angle  = 30º will be: (g = 10 m/s2)

Options

A. `13.4W`
B. 20.4W
C. 24.6W
D. zero

Answer

A

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the problem
We have a pendulum bob of mass \( m = 1 \, \text{kg} \) and length \( \ell = 1 \, \text{m} \) released from an angle of \( \theta = 60^\circ \). We need to find the power delivered by all forces acting on the bob when it reaches an angle of \( \theta = 30^\circ \).

Step 2: Identify the forces acting on the bob
The forces acting on the bob are:
1. Gravitational force (\( \vec{F_g} = m \vec{g} \))
2. Tension in the string (\( \vec{T} \))

Step 3: Calculate the gravitational force components
At \( \theta = 30^\circ \):
- The component of the gravitational force acting along the direction of motion (tangential) is given by:
\( F_{\text{tangential}} = mg \sin(30^\circ) = 1 \times 10 \times \frac{1}{2} = 5 \, \text{N} \)

Step 4: Determine the velocity of the bob at \( \theta = 30^\circ \)
Using conservation of mechanical energy:
- Initial potential energy at \( \theta = 60^\circ \):
\( h_1 = \ell (1 - \cos(60^\circ)) = 1 \times (1 - 0.5) = 0.5 \, \text{m} \)
\( PE_1 = mgh_1 = 1 \times 10 \times 0.5 = 5 \, \text{J} \)

- Final potential energy at \( \theta = 30^\circ \):
\( h_2 = \ell (1 - \cos(30^\circ)) = 1 \times (1 - \frac{\sqrt{3}}{2}) = 1 - 0.866 = 0.134 \, \text{m} \)
\( PE_2 = mgh_2 = 1 \times 10 \times 0.134 = 1.34 \, \text{J} \)

- Kinetic energy at \( \theta = 30^\circ \):
\( KE = PE_1 - PE_2 = 5 - 1.34 = 3.66 \, \text{J} \)

Using the kinetic energy formula:
\( KE = \frac{1}{2} mv^2 \implies 3.66 = \frac{1}{2} \times 1 \times v^2 \implies v^2 = 7.32 \implies v = \sqrt{7.32} \approx 2.71 \, \text{m/s} \)

Step 5: Calculate the power delivered by the forces
The power delivered by the tangential component of the gravitational force is:
\( P = F_{\text{tangential}} \cdot v = 5 \times 2.71 \approx 13.55 \, \text{W} \)

Final Answer
The power delivered by all the forces acting on the bob at angle \( \theta = 30^\circ \) is approximately \( 13.55 \, \text{W} \).

---