If f(x)=4x−3 and g(x)=x−4, which of the following has a value of −11 ?
f(g(2))
g(f(2))
g(f(3))
f(g(3))
The correct Answer is:A
To solve the problem, we need to evaluate the functions f(x)=4x−3 and g(x)=x−4 for different options to find which one equals −11.
1. Evaluate Option A: f(g(2))
- First, calculate g(2):
g(2)=2−4=−2
- Now, substitute g(2) into f:
f(g(2))=f(−2)=4(−2)−3=−8−3=−11
- Thus, f(g(2))=−11.
2. Evaluate Option B: g(f(2))
- First, calculate f(2):
f(2)=4(2)−3=8−3=5
- Now, substitute f(2) into g:
g(f(2))=g(5)=5−4=1
- Thus, g(f(2))=1.
3. Evaluate Option C: g(f(3))
- First, calculate f(3):
f(3)=4(3)−3=12−3=9
- Now, substitute f(3) into g:
g(f(3))=g(9)=9−4=5
- Thus, g(f(3))=5.
4. Evaluate Option D: f(g(3))
- First, calculate g(3):
g(3)=3−4=−1
- Now, substitute g(3) into f:
f(g(3))=f(−1)=4(−1)−3=−4−3=−7
- Thus, f(g(3))=−7.
Summary of Results:
- Option A: f(g(2))=−11
- Option B: g(f(2))=1
- Option C: g(f(3))=5
- Option D: f(g(3))=−7
The only option that has a value of −11 is Option A: f(g(2)).
- First, calculate g(2):
g(2)=2−4=−2
- Now, substitute g(2) into f:
f(g(2))=f(−2)=4(−2)−3=−8−3=−11
- Thus, f(g(2))=−11.
- First, calculate f(2):
f(2)=4(2)−3=8−3=5
- Now, substitute f(2) into g:
g(f(2))=g(5)=5−4=1
- Thus, g(f(2))=1.
- First, calculate f(3):
f(3)=4(3)−3=12−3=9
- Now, substitute f(3) into g:
g(f(3))=g(9)=9−4=5
- Thus, g(f(3))=5.
- First, calculate g(3):
g(3)=3−4=−1
- Now, substitute g(3) into f:
f(g(3))=f(−1)=4(−1)−3=−4−3=−7
- Thus, f(g(3))=−7.
- Option A: f(g(2))=−11
- Option B: g(f(2))=1
- Option C: g(f(3))=5
- Option D: f(g(3))=−7
Topper's Solved these Questions
Similar Questions
Knowledge Check
If f(x)=x3andg(x)=x2+1, which of the following is an odd functionn (are odd functions)?
I. f(x)⋅g(x)
II. f(g(x))
III. g(f(x))AOnly IBonly IIConly IIIDOnly II and IIIIf f(x)=4x+2, which of the following is the graph of f(x)?
A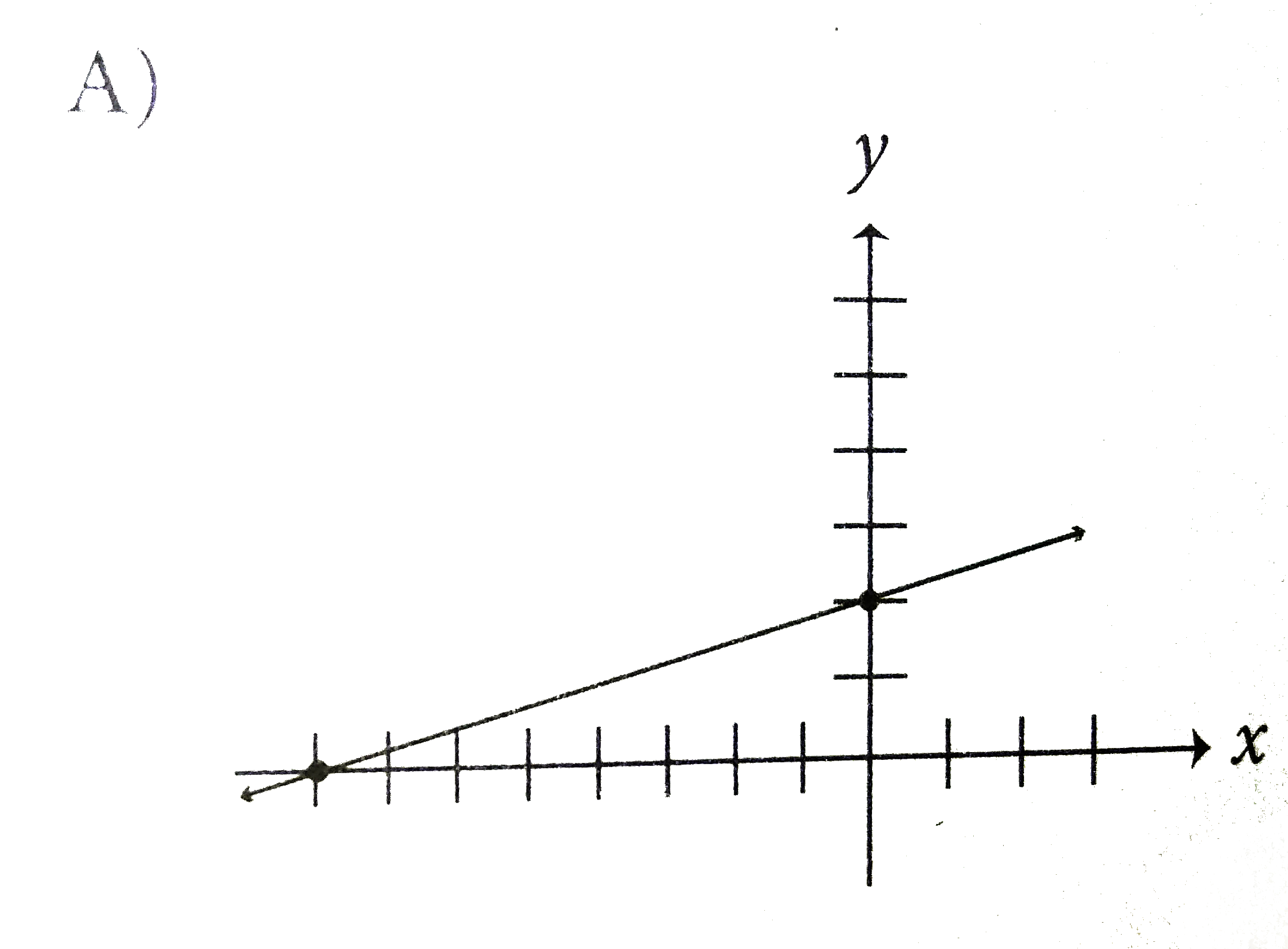 B
B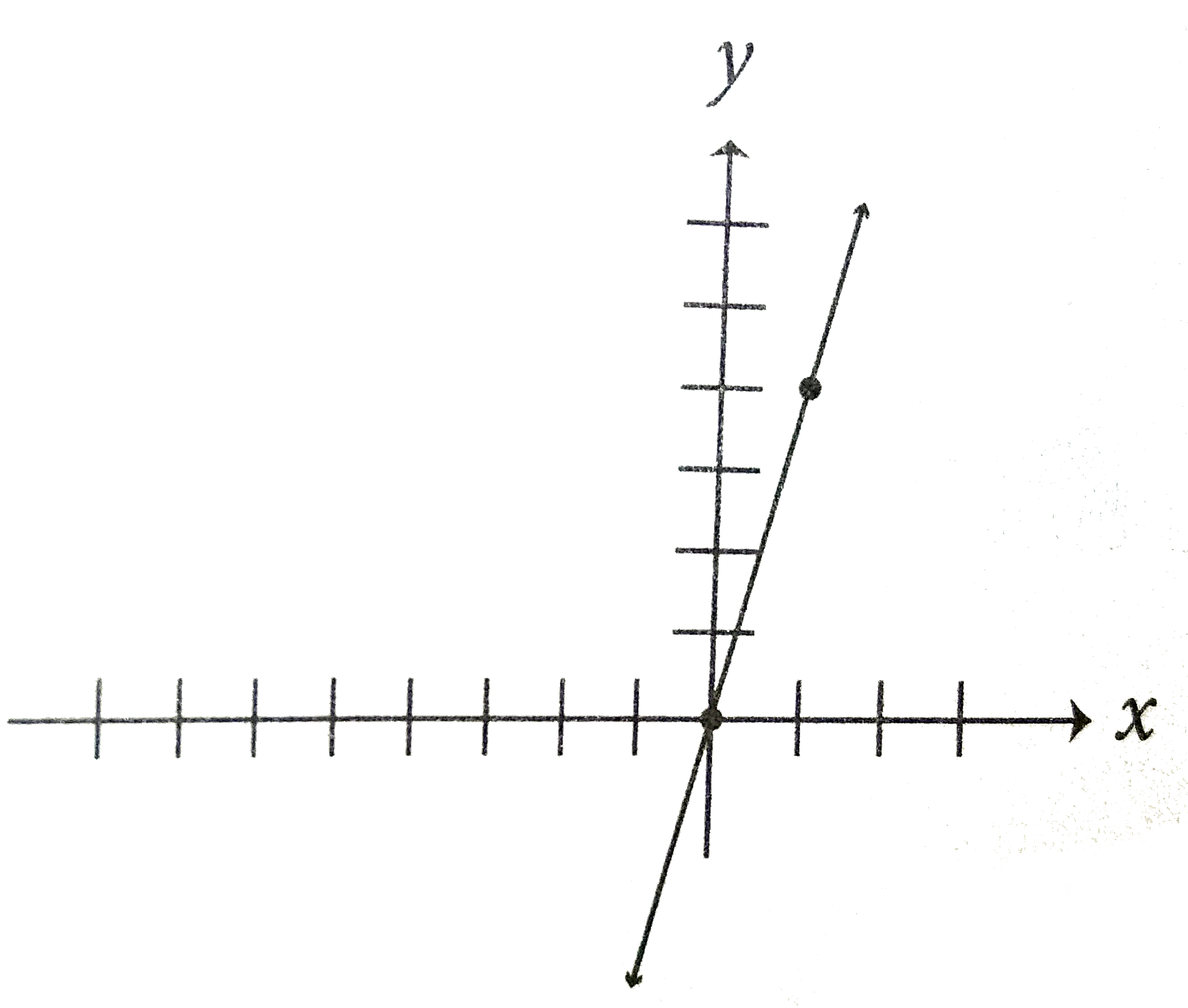 C
C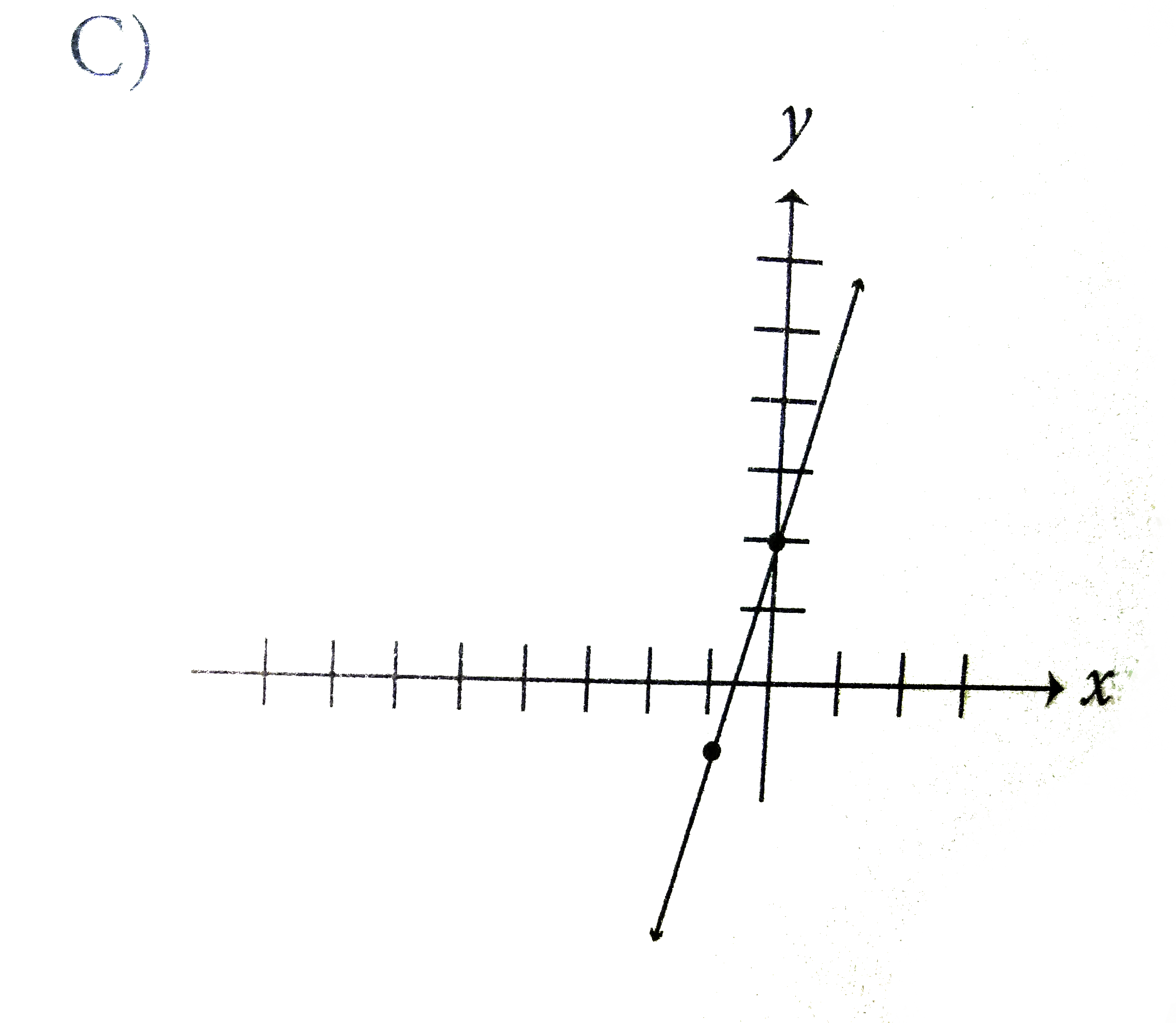 D
D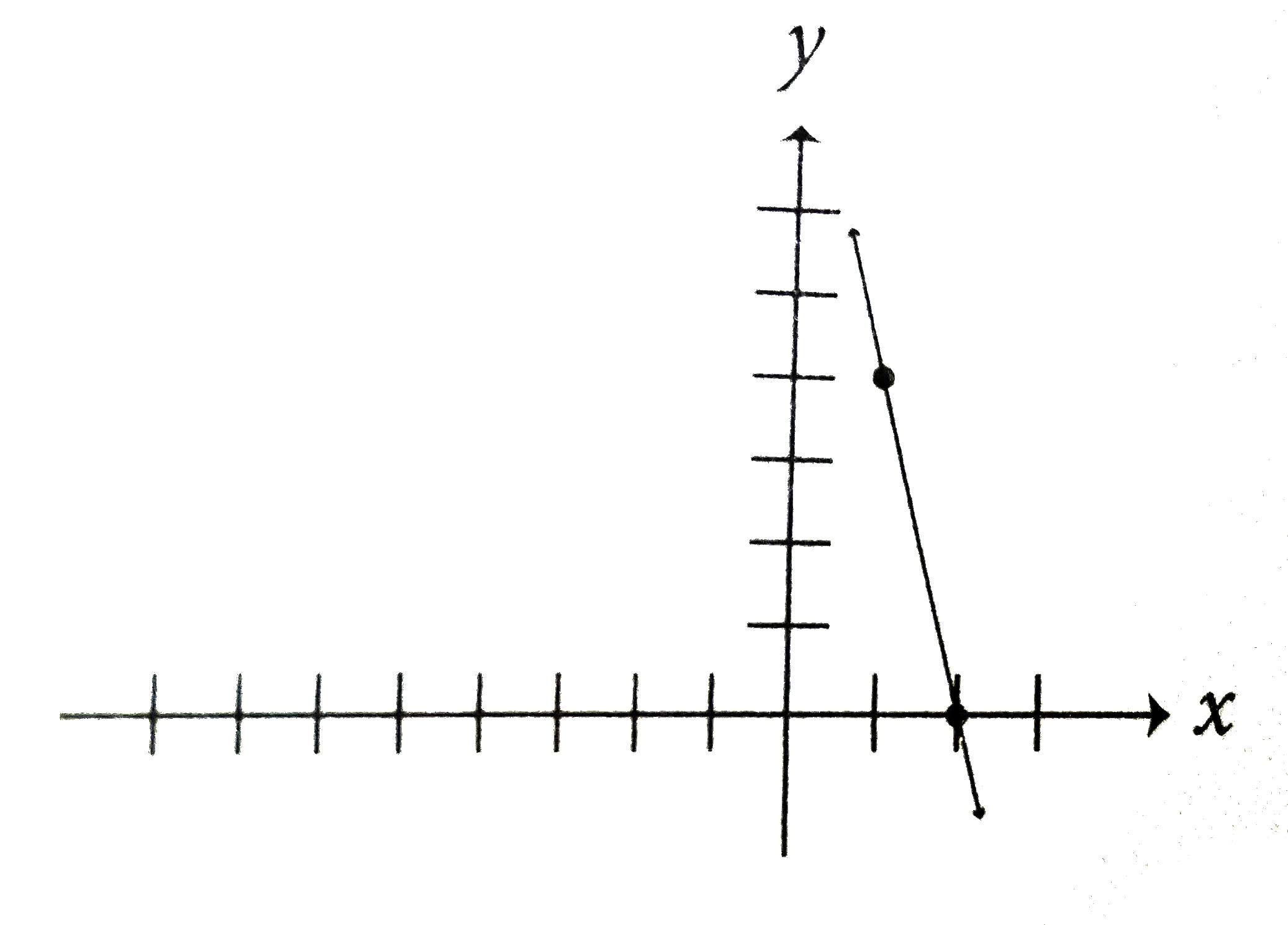
If f(x)=12x−4 and f(g(x))=g(f(x)), which of the following can be g(x) ?
I. 2x−14
II. 2x+8
III. 12x−4AI onlyBII onlyCIII onlyDII and III only
If f(x)=3x−2andg(x)=x2−4, write an expresion for each of the following functions:
(f+g)(x)
View SolutionIf f(x)=3x−2andg(x)=x2−4, write an expresion for each of the following functions:
(fg)(x)
View SolutionIf f(x)=4x−5andg(x)=3x, then f(g(2))=
View Solutionf(x)=|4x|−2x3. If f(a)=66, which of the followintg could be the value of a ?
View SolutionIf f(x)=3−xandg(x)=x22, which of the following is NOT in the range of f(g(x) ?
View Solution
