g(x+y)=g(x)+g(y)+3xy(x+y)∀x,y∈R and g'(0)=−4.
For which of the following values of x is √g(x) not defined ?
[−2,0]
[2,∞)
[−1,1]
none of these
The correct Answer is:[-1,1]
To solve the problem, we need to analyze the function g(x) defined by the equation:
g(x+y)=g(x)+g(y)+3xy(x+y)
We also know that g′(0)=−4.
Step 1: Differentiate the given equation
We start by differentiating both sides of the equation with respect to x:
ddx(g(x+y))=ddx(g(x)+g(y)+3xy(x+y))
Using the chain rule on the left side and the product rule on the right side, we get:
g′(x+y)=g′(x)+3y(x+y)+3xy
Step 2: Substitute x=0
Now, we substitute x=0:
g′(y)=g′(0)+3y(0+y)+0
Given g′(0)=−4, we have:
g′(y)=−4+3y2
Step 3: Integrate to find g(y)
Next, we integrate g′(y) to find g(y):
g(y)=∫(−4+3y2)dy=−4y+y3+C
Where C is a constant.
Step 4: Find g(0)
To find the constant C, we can use the original equation by setting x=0 and y=0:
g(0)=g(0)+g(0)+0
This implies g(0)=0. Therefore, we set g(0)=−4(0)+03+C=0, which gives C=0.
Step 5: Write the final form of g(x)
Thus, we have:
g(x)=−4x+x3
Step 6: Find when √g(x) is not defined
The expression √g(x) is not defined when g(x)<0. We need to find the values of x for which:
−4x+x3<0
This can be rearranged to:
x3−4x<0
Factoring gives:
x(x2−4)<0⇒x(x−2)(x+2)<0
Step 7: Analyze the intervals
To find the intervals where this inequality holds, we can analyze the sign changes around the roots x=−2,0,2:
- For x<−2: All factors are negative, so the product is negative.
- For −2<x<0: x is negative, (x−2) is negative, (x+2) is positive, so the product is positive.
- For 0<x<2: x is positive, (x−2) is negative, (x+2) is positive, so the product is negative.
- For x>2: All factors are positive, so the product is positive.
Thus, g(x)<0 in the intervals (−∞,−2) and (0,2).
Conclusion
The values of x for which √g(x) is not defined are:
- x∈(−∞,−2)
- x∈(0,2)
- For −2<x<0: x is negative, (x−2) is negative, (x+2) is positive, so the product is positive.
- For 0<x<2: x is positive, (x−2) is negative, (x+2) is positive, so the product is negative.
- For x>2: All factors are positive, so the product is positive.
- x∈(0,2)
Topper's Solved these Questions
- DIFFERENTIATIONBook:CENGAGE ENGLISHChapter:DIFFERENTIATIONExercise:Matrix Match Type
Explore 6 Videos
- DIFFERENTIATIONBook:CENGAGE ENGLISHChapter:DIFFERENTIATIONExercise:Numerical Value Type
Explore 45 Videos
- DIFFERENTIATIONBook:CENGAGE ENGLISHChapter:DIFFERENTIATIONExercise:Multiple Correct Answers Type
Explore 29 Videos
- DIFFERENTIAL EQUATIONSBook:CENGAGE ENGLISHChapter:DIFFERENTIAL EQUATIONSExercise:Matrix Match Type
Explore 5 Videos
- DOT PRODUCTBook:CENGAGE ENGLISHChapter:DOT PRODUCTExercise:DPP 2.1
Explore 15 Videos
Similar Questions
Knowledge Check
The functions r is defined as g(x)=x23−|x−4|. For which values of x is g(x) NOT defined?
Ax=4 and x=7Bx=3 and x=4Cx=3 and x=7Dx=1 and x=7
Let g:R→R be a differentiable function satisfying g(x)=g(y)g(x−y)∀x,y∈R and g′(0)=aandg′(3)=b. Then find the value of g′(−3).
View SolutionLet g:R→R be a differentiable function satisfying g(x)=g(y)g(x−y)∀x,y∈R and g′(0)=aandg′(3)=b. Then find the value of g′(−3).
View SolutionLet y=f(x) such that xy=x+y+1,x∈R−{1}andg(x)=xf(x)
The minimum value of g(x) is:
View SolutionLet f(x+y)=f(x)+f(y) and f(x)=x2g(x)∀x,y∈R where g(x) is continuous then f'(x) is
View SolutionLet f:R→R be a continous and differentiable function such that f(x+y)=f(x).F(y)∀x,y,f(x)≠0andf(0)=1andf'(0)=2.
Let g(xy)=g(x).g(y)∀x,yandg'(1)=2.g(1)≠=0
The number of values of x, where f(x)g(x):
View SolutionGraph of y=f(x)andy=g(x) is given in the following figure. If h(x)=f(g(x)), then find the value of h'(2).
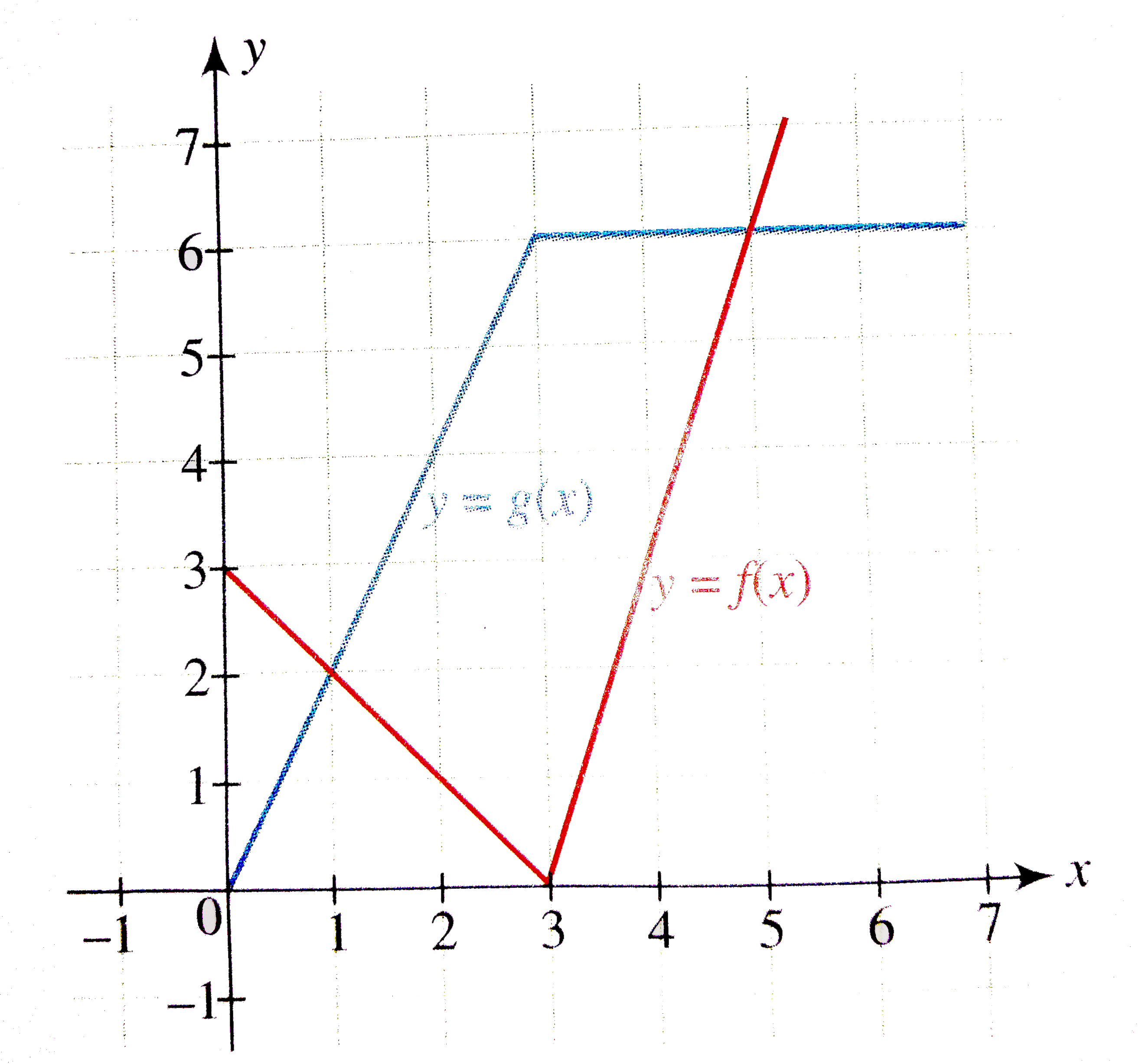
View SolutionIf f(x−y)=f(x).g(y)−f(y).g(x) and g(x−y)=g(x).g(y)+f(x).f(y) for all x∈R . If right handed derivative at x=0 exists for f(x) find the derivative of g(x) at x =0
View Solution