If , then =
3
9
27
31
The correct Answer is:D
To solve the problem, we need to find the value of f(g(2)) given the functions f(x)=4x−5 and g(x)=3x.
1. Calculate g(2):
g(x)=3x
Substitute x=2:
g(2)=32=9
2. Substitute g(2) into f(x):
Now we need to find f(g(2)), which is f(9):
f(x)=4x−5
Substitute x=9:
f(9)=4×9−5
3. Calculate f(9):
f(9)=36−5=31
Thus, the final answer is:
f(g(2))=31
g(x)=3x
Substitute x=2:
g(2)=32=9
Now we need to find f(g(2)), which is f(9):
f(x)=4x−5
Substitute x=9:
f(9)=4×9−5
f(9)=36−5=31
f(g(2))=31
Topper's Solved these Questions
Similar Questions
If {(3,2),(4,2),(3,1),(7,1),(2,3)} is to be a function, which one of the following must be removed from the set?
View SolutionIf xa⋅(xa+1)a⋅(xa)1−a=xk, then k=
View Solution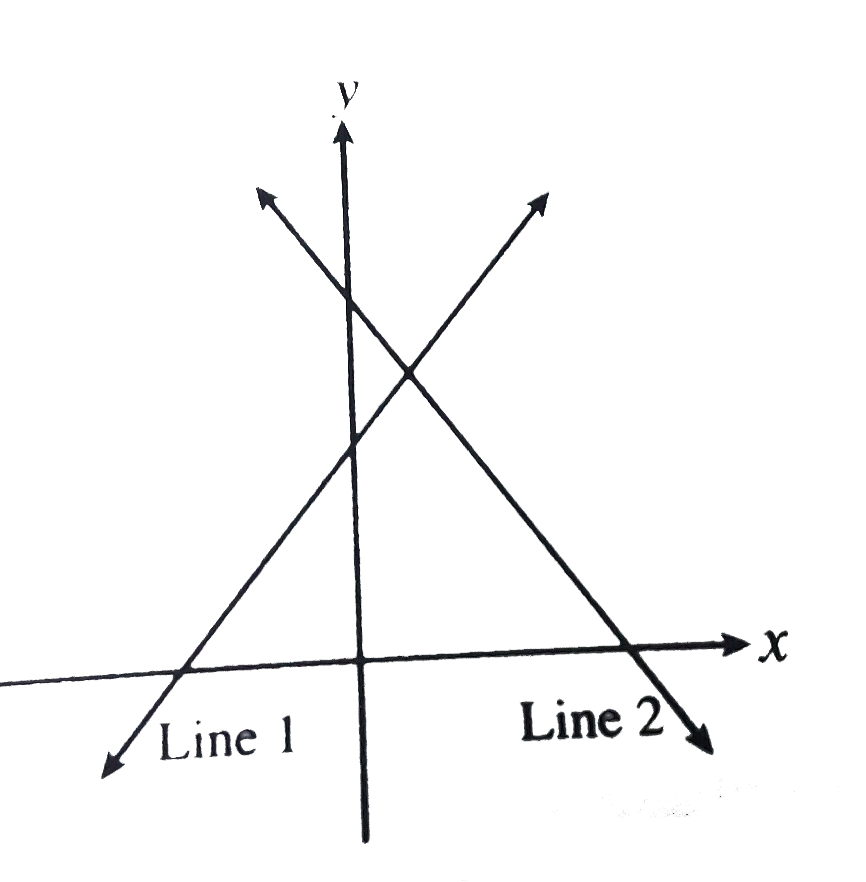
Consider two lines in the xy-plane , as shown above. If line 1 has equation y=m1x+b1, and line 2 has equation y=m2x+b2. Which is a true statement ?
View SolutionSuppose thath (x)=f(x).g(x) and F(x)=f(g(x))f(2)=3;g(2)=5;g(2)=4;f(2)-=2 and f'(5)=11 then
View SolutionLet f(x)=x^(2)-4x-3,x>2 and let g be the inverse of f. Find the value of g', where f(x)=2
View SolutionThe solution set of f'(x)>g'(x) where f(x)=((1)/(2))5^(2x+1) and g(x)=5^(x)+4x log5
View SolutionThe solution set of f'(x)>g'(x) where f(x)=((1)/(2))5^(2x+1) and g(x)=5^(x)+4x log5
View SolutionIf f(g(x)) = g(f(x)) = x for all real numbers x, and f(2) = 5 and f(5) = 3, then the value of g(3)+ g(f(2)) is
View SolutionQ.5 If f(g(x))=g(f(x))=x for all real numbers x, and f(2)=5 and f(5)=3, then the value g(3)+g(f(2)) is
View SolutionIf g(x)=x2+x+x−1andg(f(x))=4x2−10x+5 then find f(54)
View SolutionIf f(x)=4x2 and g(x) =f(sin x)+f(cos x), then g(23∘) is
View SolutionIf g(x)=x3+x−2 and g(f(x))=x3+3x2+4x then f(1)+f(2) is equal to ________
View SolutionIf the function f(x)=4x5+3x3+2x2+ex7 and g(x)=f−1(x) then the value of g'(1) is
View SolutionIf the function f(x)=4x5+3x3+2x2+ex7 and g(x)=f−1(x) then the value of g'(1) is
View SolutionLet f(x)=x2−4x−3,x>2 and g(x) be the inverse of f(x). Then the value fo(g'), where f(x)=2, is (here, g' represents the first derivative of g)
View Solution

