If f(x)=x, the inverse of f,f−1, could be represented by
f−1(x)=x
f−1(x)=1
f−1(x)=1x
f−1(x)=y
The correct Answer is:A
To find the inverse of the function f(x)=x, we can follow these steps:
Step 1: Replace f(x) with y
We start by rewriting the function:
y=f(x)=x
Step 2: Solve for x in terms of y
In this case, since y=x, we can directly see that:
x=y
Step 3: Express the inverse function
Now we can express the inverse function. Since we have x=y, we can write:
f−1(y)=x
Substituting y back with x gives us:
f−1(x)=x
Conclusion
Thus, the inverse of the function f(x)=x is:
f−1(x)=x
Final Answer
The inverse function f−1 could be represented by f−1(x)=x.
---
We start by rewriting the function:
y=f(x)=x
In this case, since y=x, we can directly see that:
x=y
Now we can express the inverse function. Since we have x=y, we can write:
f−1(y)=x
Substituting y back with x gives us:
f−1(x)=x
Thus, the inverse of the function f(x)=x is:
f−1(x)=x
The inverse function f−1 could be represented by f−1(x)=x.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If f(x)=2x−3, the inverse of f,f−1 could be represented by
Af−1(x)=3x−2Bf−1(x)=12x−3Cf−1(x)=x−23Df−1(x)=x+32If f(x)=x3−4, then the inverse of f=
A−x3+4B3√x+4C3√x−4D1x3−4If f(x)−1x, then f(a)+f(1a)=
A0B2a−2aCa−1aDa4−a2+1a(a2−1)
Find the inverse of f(x)=⎧⎪⎨⎪⎩xx<1x21≤x≤48√xx>4
View SolutionLet f:A→Bf(x)=x+abx2+cx+2, where A represent domain set and B represent range set of function f(x) a,b,c ∈R,f(−1)=0andy=1 is an asymptote of y=f(x)andy=g(x) is the inverse of f(x).
Area of region enclosed by asymptotes of curves y=f(x)andy=g(x) is:
View SolutionLet f:A→Bf(x)=x+abx2+cx+2, where A represent domain set and B represent range set of function f(x) a,b,c ∈R,f(−1)=0andy=1 is an asymptote of y=f(x)andy=g(x) is the inverse of f(x).
g (0) is equal to :
View SolutionIf f(x)=1−4x, and f−1(x) is the inverse of f(x), then f(−3)f−1(−3)=
View SolutionThe graph of y=f(x) is shown to the right. If f(−1)=v, then which one of the following could be the value of f(v) ?
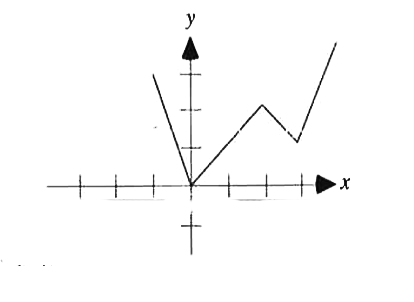
View Solution

