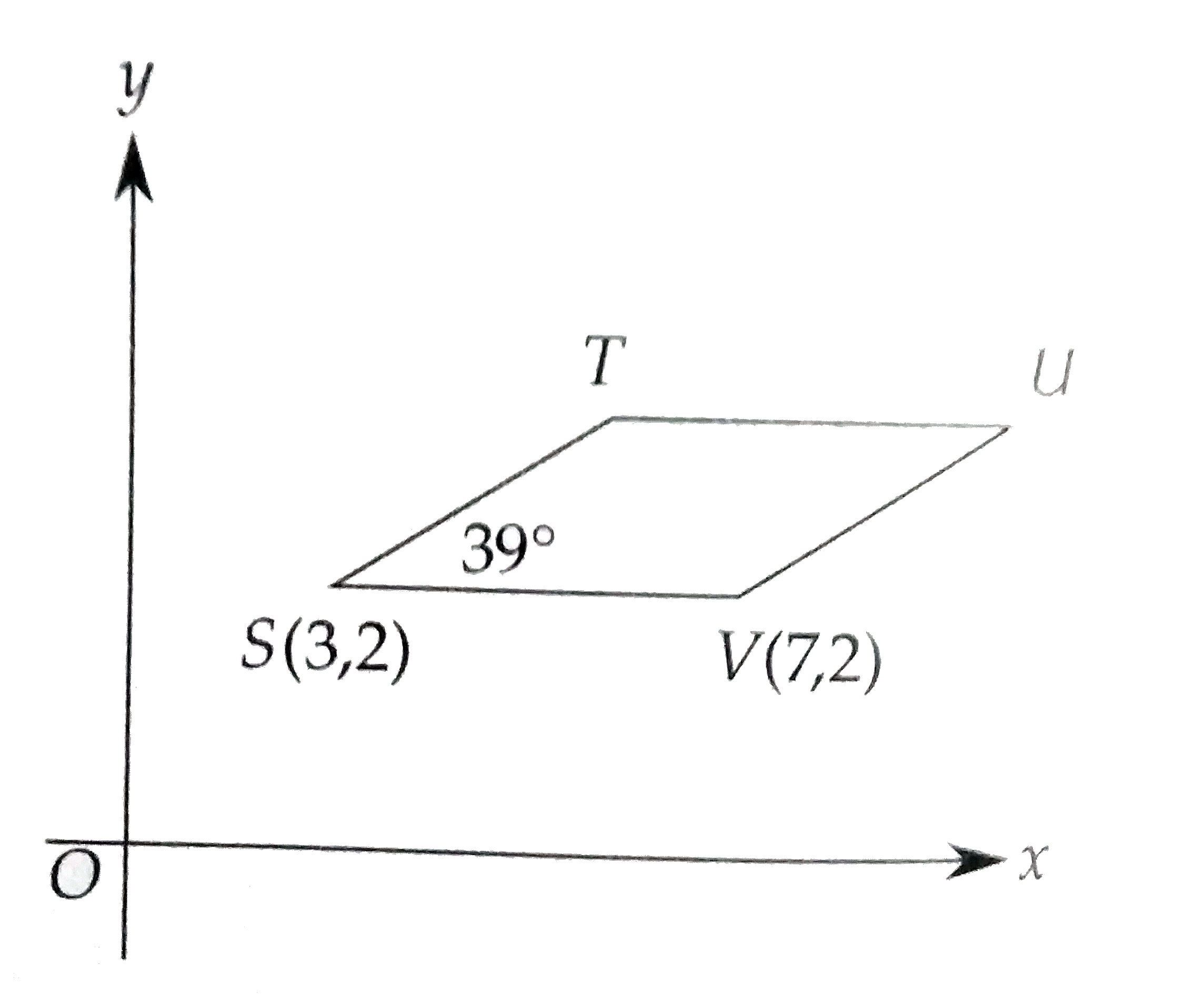
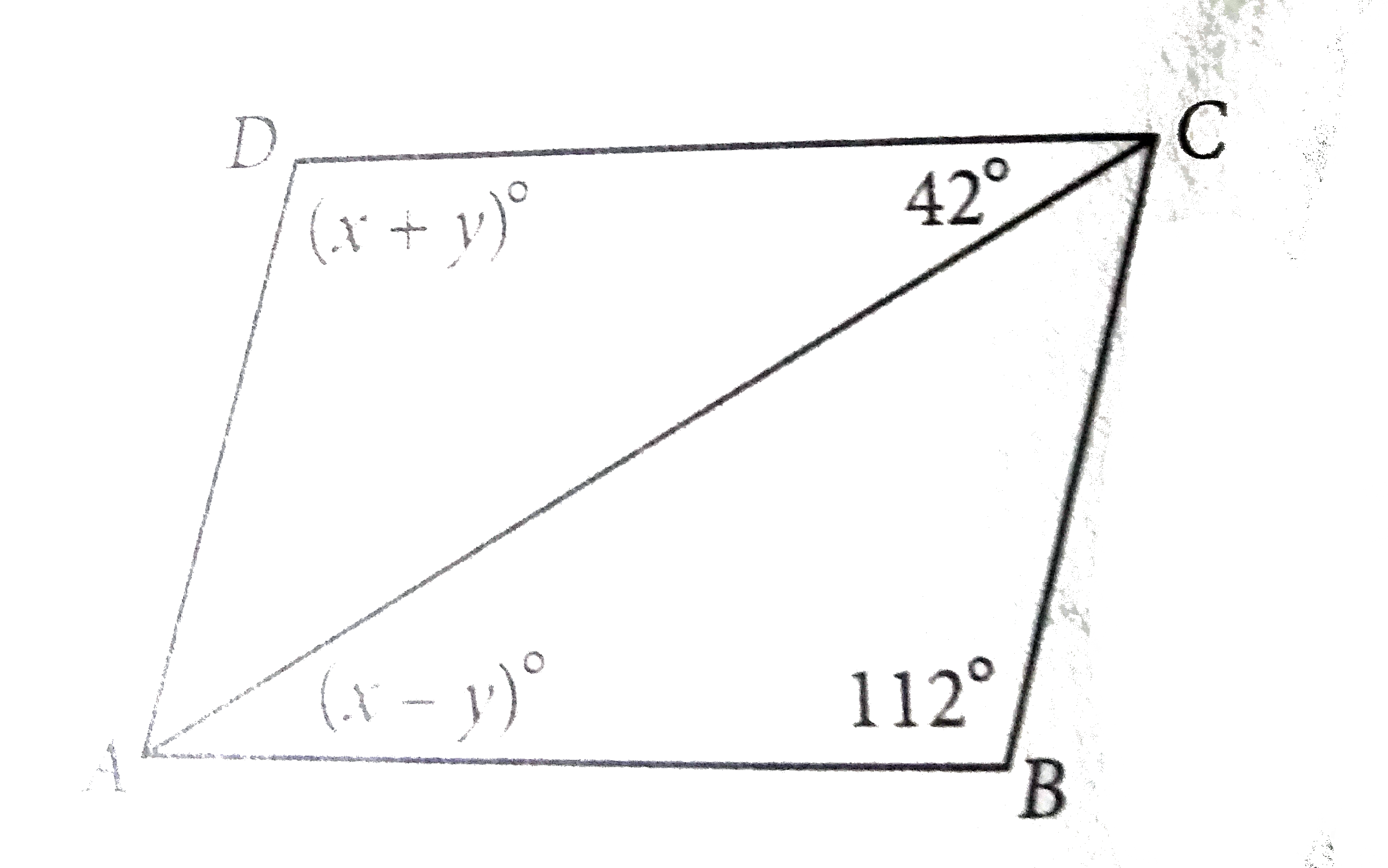In Figure STUV is a parallelogram with a perimeter of 14. What is the y - coordinate of point T ?
A
1.26
B
1.89
C
3.26
D
3.89
Video Solution
Text Solution
The correct Answer is:D
The perimeter of any polygon is the sum of the lengths of its sides. Since points S and V have the same y - coordinate of 2, SV is parallel to the x - axis. The length of SV is the positive difference of the x - coordinates of points V and S. The length of SV is 7−3=4. Opposite sides of a parallelogram are equal, so the length of TU is also 4. ST and UV are opposite sides of parallelogram STUV, so ST and UV also have equal lengths. The perimeter of the parallelogram is 2(4)+2(ST). So 2(4)+2(ST)=14,8+2(ST)=14,(ST)=6, and ST = 3. Drop a perpendicular line from point T to SV that meets side SV at point P.
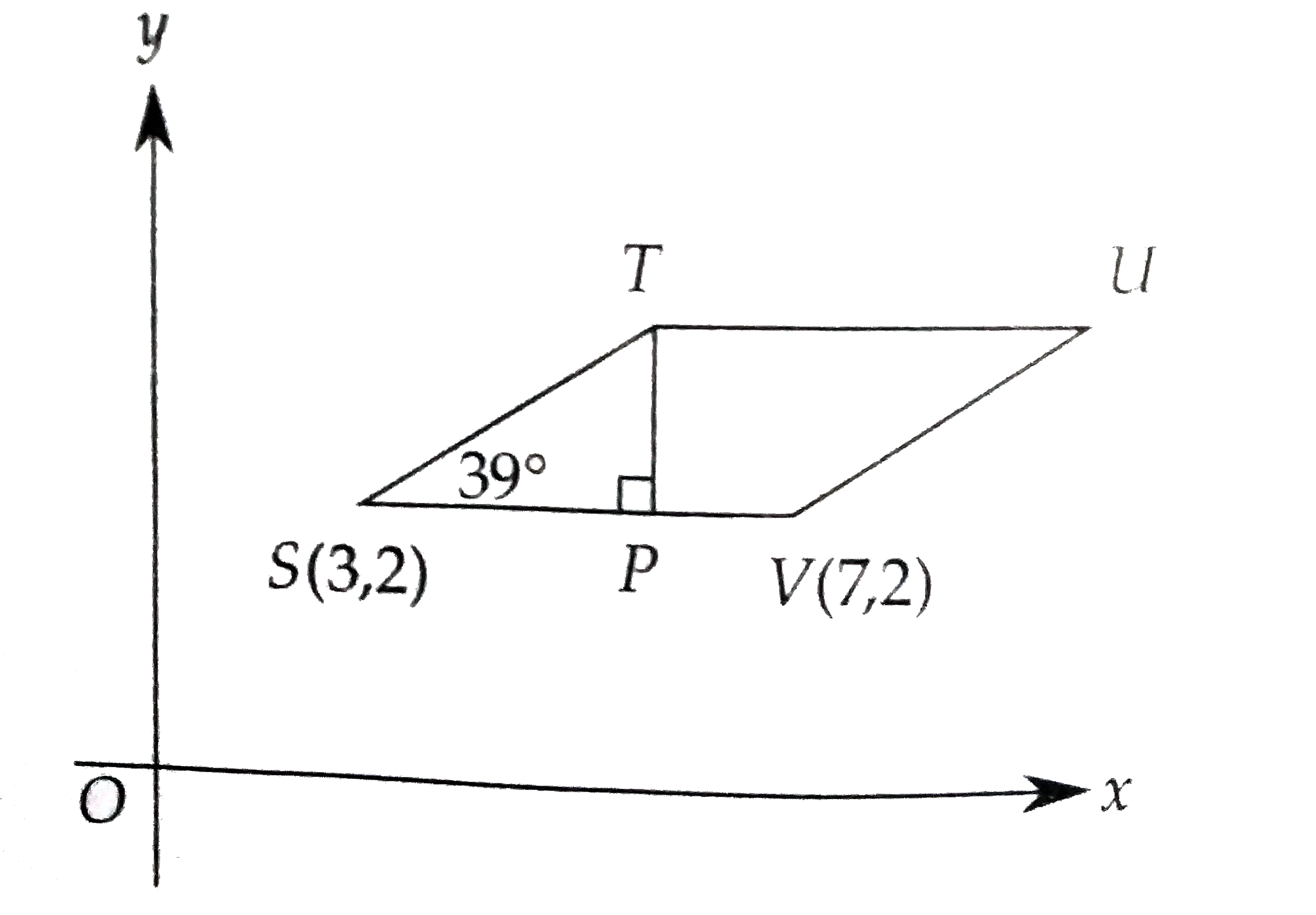
Since point P is on segment SV, the y - coordinate of point P is also 2. Then the y - coordinate of point T is equal to 2 plus the length of TP. Now sin 39∘=TPST. Since ST=3,sin39∘=TP3, so TP=3sin90∘.
The y - coordinate of T is 2+3sin39∘≈3.89.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, ABCD is a parallelogram, what is the value of b?
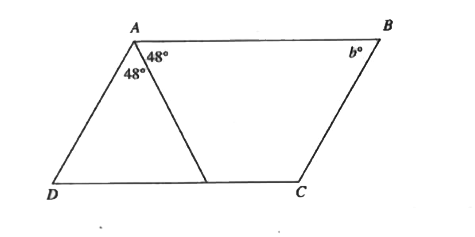 A46B48C72D84
A46B48C72D84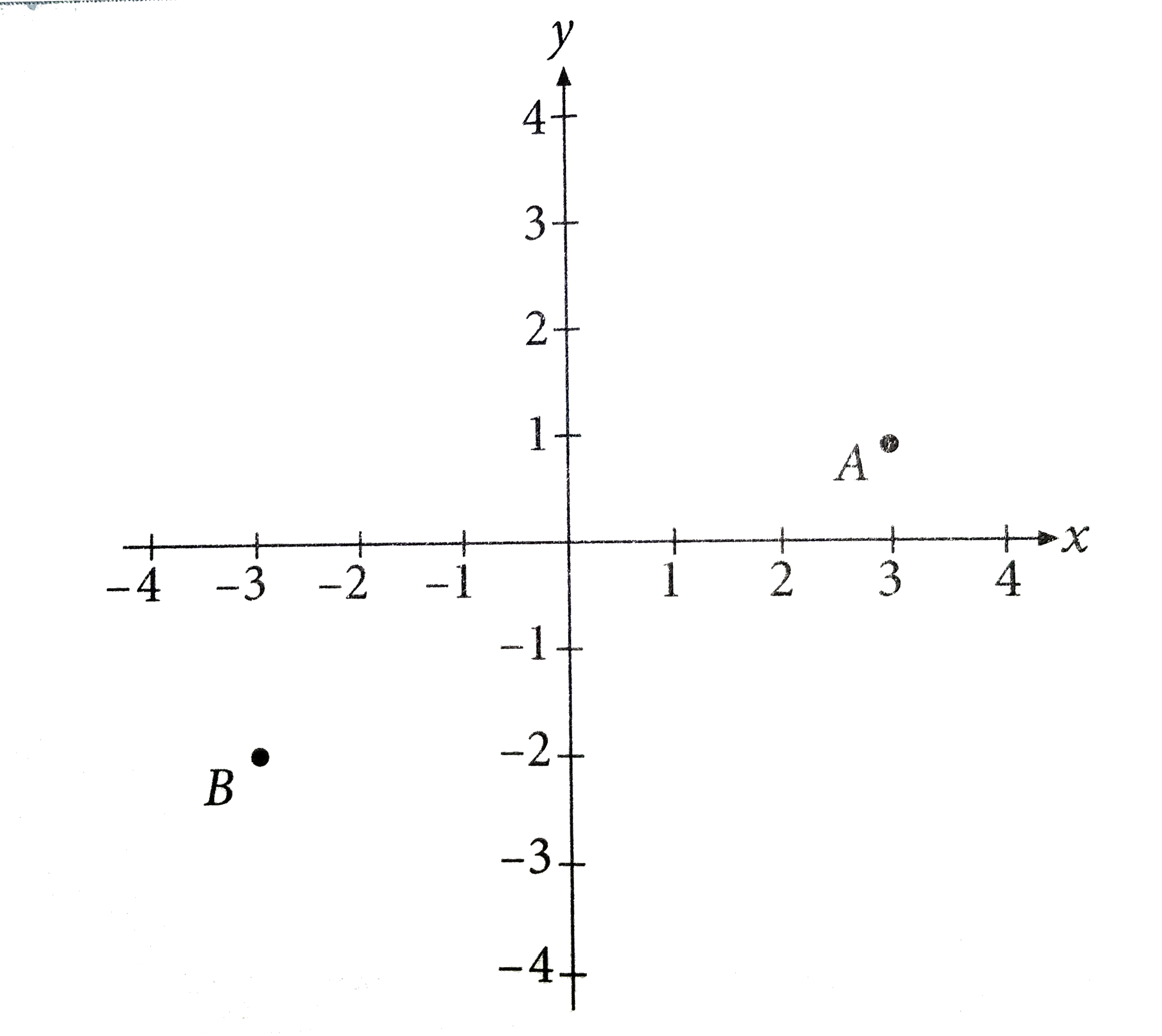
In the xy-plane above, what is the value of the x-coordinates of Point A minus the y-coordinates of Point B?A−2B−1C3D5What is the perimeter of ΔABC shown in the figure?
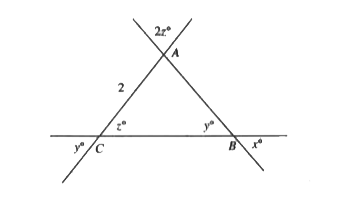 A2+4√2B4+2√2C8D4+4√2
A2+4√2B4+2√2C8D4+4√2
In figure LM is a line parallel to the Y-axis at a distance of 3 units .
(i) What are the coordinates of the points P,R and Q ?
(ii) What is the difference between the abscissa of the points L and M ?
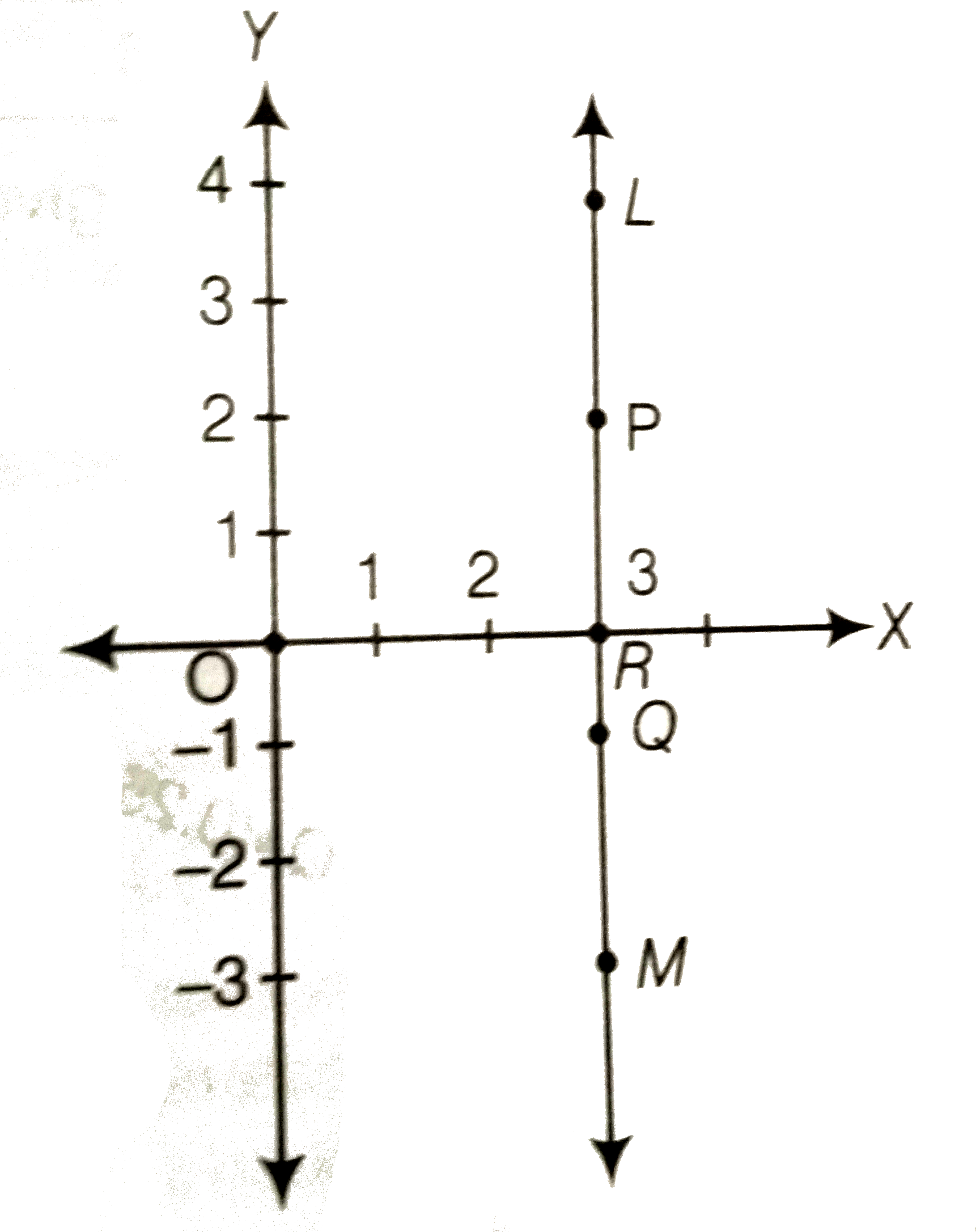
View SolutionIn Figure, RICE is parallelogram. Find x, y, z.
View SolutionIn the given figure, ABCD is a parallelogram. Find the values of x, y and z
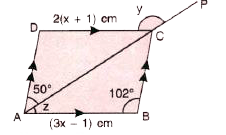
View SolutionWhat is the perimeter of the parallelogram ?
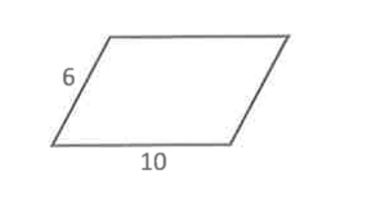
View SolutionThe equation (x+4)2+(y−7)2=25 represents a circle in the xy-plane . Points A and B on the circle are the endpoints of diameter, and point A has coordinates (-4, 2). What are the coordinates of point B?
View Solution