The equation (x+4)2+(y−7)2=25 represents a circle in the xy-plane . Points A and B on the circle are the endpoints of diameter, and point A has coordinates (-4, 2). What are the coordinates of point B?
(−9,7)
(−4,12)
(−4,7)
(1,7)
The correct Answer is:C
To find the coordinates of point B, we will follow these steps:
Step 1: Identify the center and radius of the circle
The equation of the circle is given as:
(x+4)2+(y−7)2=25
This can be compared to the standard form of a circle's equation:
(x−h)2+(y−k)2=r2
where (h,k) is the center and r is the radius.
From the given equation, we can see:
- h=−4
- k=7
- r2=25 which gives r=5
Step 2: Find the coordinates of point A
We are given that point A has coordinates:
A(−4,2)
Step 3: Determine the coordinates of point B
Since A and B are endpoints of the diameter of the circle, the center of the circle is the midpoint of segment AB. The coordinates of the center (h, k) can be calculated as:
(xA+xB2,yA+yB2)=(h,k)
Substituting the known values:
(−4+xB2,2+yB2)=(−4,7)
Step 4: Set up the equations
From the x-coordinates:
−4+xB2=−4
Multiplying both sides by 2:
−4+xB=−8
Solving for xB:
xB=−8+4=−4
From the y-coordinates:
2+yB2=7
Multiplying both sides by 2:
2+yB=14
Solving for yB:
yB=14−2=12
Step 5: Write the coordinates of point B
Thus, the coordinates of point B are:
B(−4,12)
Summary
The coordinates of point B are (−4,12).
---
The equation of the circle is given as:
(x+4)2+(y−7)2=25
This can be compared to the standard form of a circle's equation:
(x−h)2+(y−k)2=r2
where (h,k) is the center and r is the radius.
- h=−4
- k=7
- r2=25 which gives r=5
We are given that point A has coordinates:
A(−4,2)
Since A and B are endpoints of the diameter of the circle, the center of the circle is the midpoint of segment AB. The coordinates of the center (h, k) can be calculated as:
(xA+xB2,yA+yB2)=(h,k)
Substituting the known values:
(−4+xB2,2+yB2)=(−4,7)
From the x-coordinates:
−4+xB2=−4
Multiplying both sides by 2:
−4+xB=−8
Solving for xB:
xB=−8+4=−4
2+yB2=7
Multiplying both sides by 2:
2+yB=14
Solving for yB:
yB=14−2=12
Thus, the coordinates of point B are:
B(−4,12)
The coordinates of point B are (−4,12).
Topper's Solved these Questions
- PROBLEM SETSBook:PRINCETONChapter:PROBLEM SETSExercise:PROBLEM SET 11: TRIANGLES
Explore 11 Videos
- PROBLEM SETSBook:PRINCETONChapter:PROBLEM SETSExercise:PROBLEM SET 12: CIRCLES, QUADRILATERALS, AND VOLUME
Explore 11 Videos
- PROBLEM SETSBook:PRINCETONChapter:PROBLEM SETSExercise:PROBLEM SET 9: EXPONENTS, ROOTS, AND EQUATIONS
Explore 11 Videos
- PRACTICE TEST 4Book:PRINCETONChapter:PRACTICE TEST 4Exercise:Math Test-Calculator
Explore 38 Videos
- SAT MATH: THE BIG PICTUREBook:PRINCETONChapter:SAT MATH: THE BIG PICTUREExercise:Example
Explore 4 Videos
Similar Questions
The point (p,0) lies on a circle in the xy-plane. The points (2,3.5) and (-2,0.5) are the endpoints of a diameter of the circle . If p>0, what is the value of p?
View SolutionThe line represented by the equation y=−2x+6 is the perpendicular bisector of the line segment AB. If A has the coordinates (7,2), what are the coordinates for B?
View Solution
Knowledge Check
The equation (x−7)2+(y−8)2=10 is that of a circle that lies in the standard (x,y) coordinate plane. One endpoint of a diameter of the circle has y-coordinate 11. What is the y-coordinate of the other endpoint of that diameter?
A1B3C4D5Line segment ¯¯¯¯¯¯AB has midpoint (7,-1) . If point A has coordinates (2,6) , then point B has coordinates
A(92,52)B(192,−92)C(12,-8)D(14,-8)
Point K is the center of the circle above, and the coordinates of Point K are (2, -1). What is the area of the circle?AπB2πC4πD8π
Find the equation of the circle, the coordinates of the end points of whose diameter are (−1,2)and(4,−3).
View SolutionThe center of circle Q has coordinates (3,−2) in the xy-plane. If an endpoint of a radius of circle Q has coordinates R(7,1), what is the equation of circle Q?
View Solution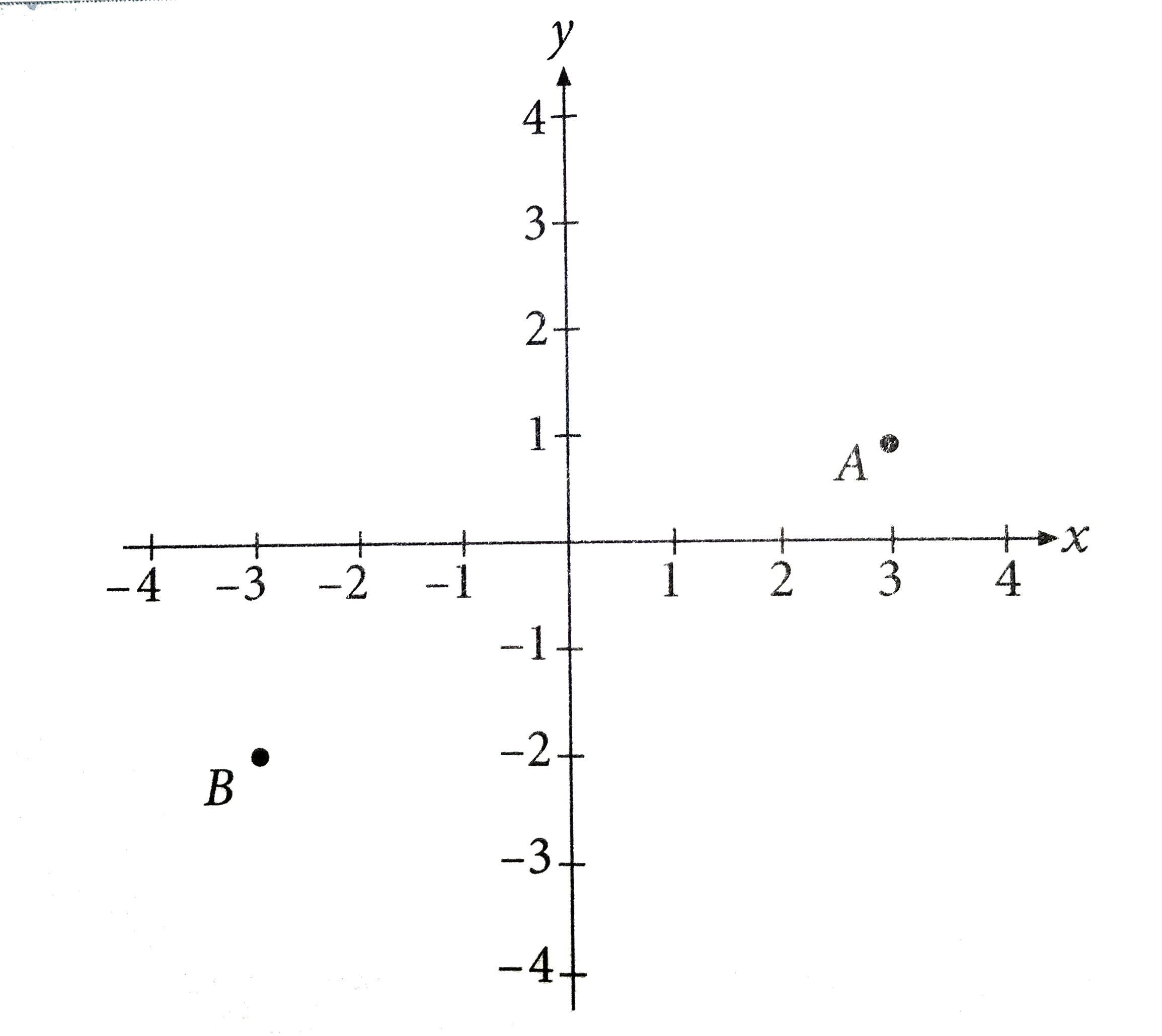
In the xy-plane above, what is the value of the x-coordinates of Point A minus the y-coordinates of Point B?
View SolutionWhen points A and B (-3, 4) are graphed in the standard (x,y) coordinate plane below, the midpoint of ¯¯¯¯¯¯AB will be (1,2). What will be the coordinate of point A?

View Solutionx2+y2+4x−2y=−1
The equation of a circle in the xy-plane is shown above. What is the radius of the circle?
View Solution

