Question

The greatest possible distance between any two points on the surface of a right circular cylinder is $\sqrt{193}$ and the area of the circular base of the right circular cylinder is $36\pi$. What is the volume of the right circular cylinder ?

Options

A. `252 pi`
B. `294 pi`
C. `343 pi`
D. `386 pi`

Answer

A

Explanation

The volume of a right circular cylinder having a radius r and a height h is `pi r^(2)h`. To find the volume of this right circular cylinder, you need its radius and its height. Now the area of a circle with a radius r is `pi r^(2)`. The area of the circular base is `36pi`. If the radius of the circular base is r, then `pi r^(2)=36pi, r^(2)=36`, and r = 6. You now have the radius. Thediameter is 2(6) = 12. Let's call the height of the right circular cylinder h and draw a picture.

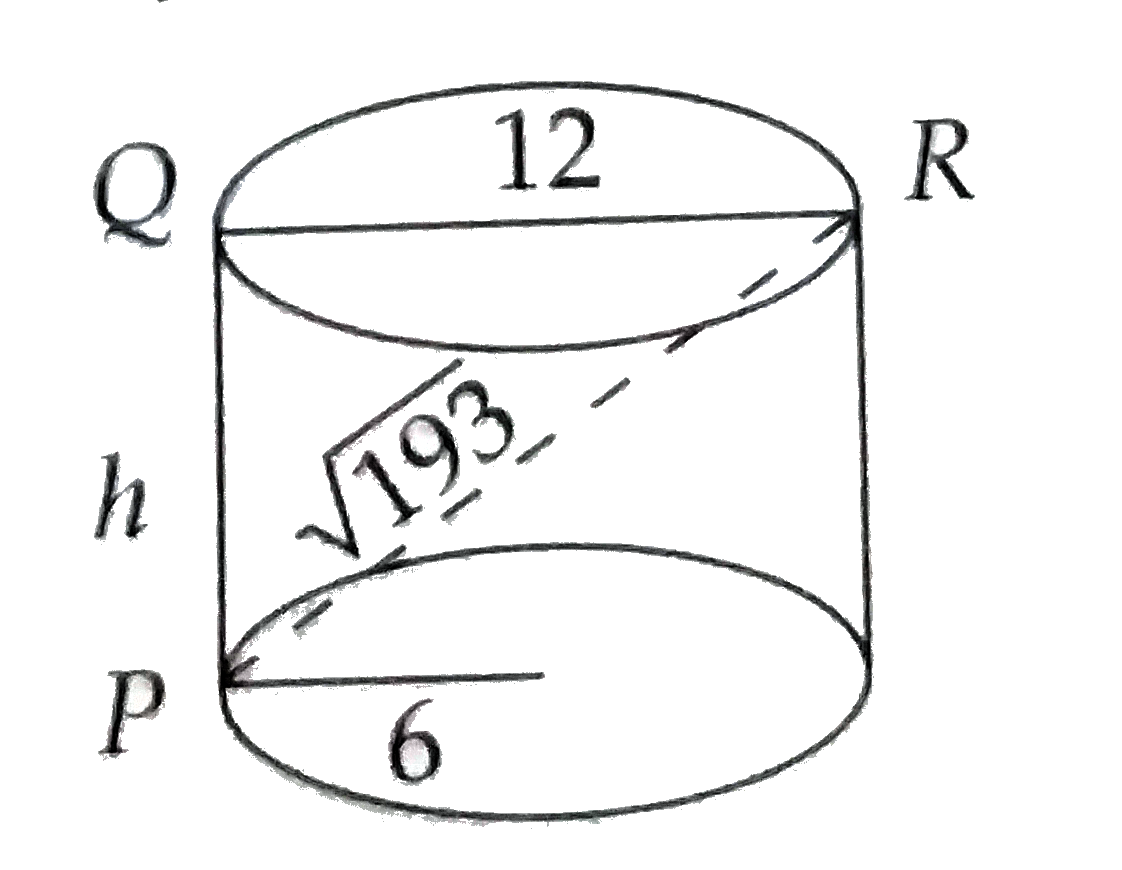
The greatest possible distance between two points on the surface of the right circular cylinder is the distance between points P and R. Use the Pythagorean theorem in right triangle PQR to find the height h.
`12^(2)+h^(2)=(sqrt(193))^(2)`
`144+h^(2)=193`
`h^(2)=49`
h = 7
The volume of the right circular cylinder is `pi r^(2)h=pi(6^(2))(7)=pi(36)(7)=252 pi`.