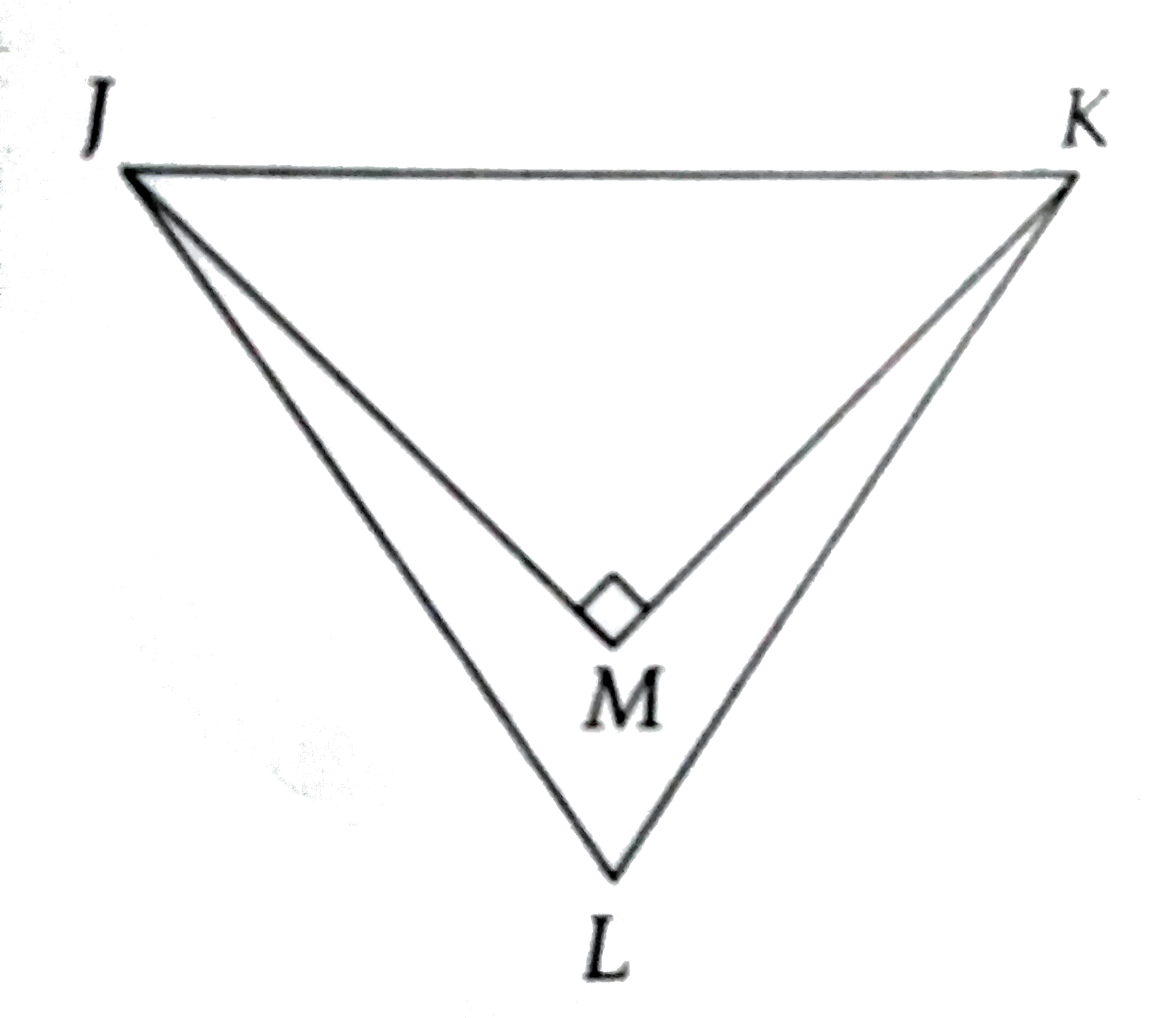
ΔJKL is equilateral, and ΔJKM is isosceles. If ¯¯¯¯¯¯KL=2, what is the distance from L to M ?
0.572
0.636
0.667
0.732
The correct Answer is:D
To get the answer to this question, you need to know about equilateral, 45-45-90, and 30-60-90 triangles. If you drop an altitude from a new point, N, through M to L, you you will divide the equilateral triangle into two 30-60-90 triangles and divide the right isosceles (or 45-45-90) triangle into two smaller right into two smaller right isosceles triangles :
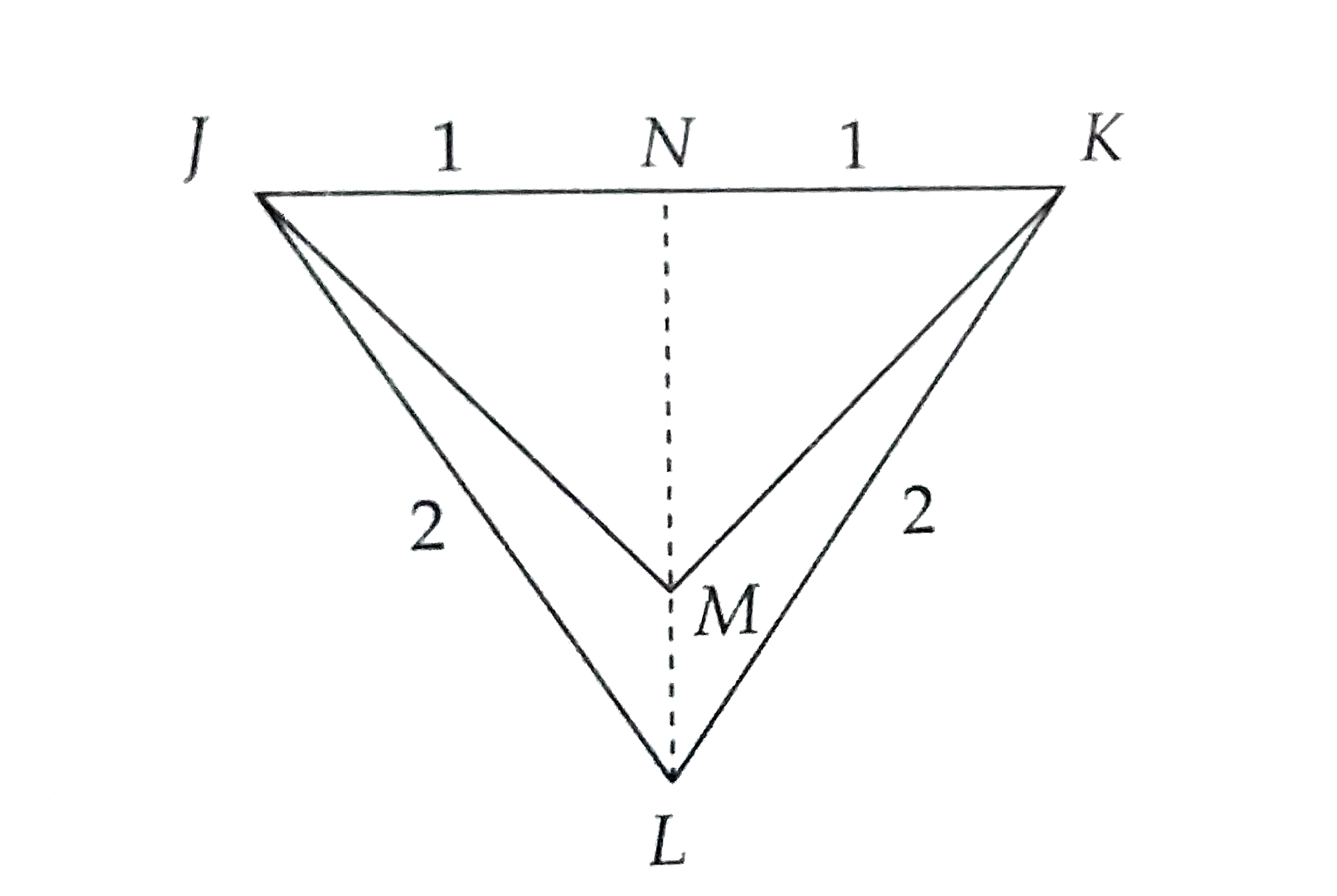
Using the side ratios for 30-60-90s and 45-45-90s, you know that ¯¯¯¯¯¯LN=√3 and that ¯¯¯¯¯¯¯¯MN=1.
Therefore, ¯¯¯¯¯¯¯LM=¯¯¯¯¯¯LN−¯¯¯¯¯¯¯¯MN=√3−1≈1.732−1=0.732.
Topper's Solved these Questions
- PLANE GEOMETRY Book:KAPLANChapter:PLANE GEOMETRY Exercise:PLANE GEOMETRY FOLLOW - UP TEST
Explore 6 Videos
- MISCELLANEOUS TOPICS Book:KAPLANChapter:MISCELLANEOUS TOPICS Exercise:MISCELLANEOUS TOPICS FOLLOW - UP TEST
Explore 12 Videos
- PRACTICE TEST 1 Book:KAPLANChapter:PRACTICE TEST 1 Exercise:PRACTICE TEST
Explore 50 Videos
Similar Questions
Knowledge Check
In the diagram below ,ΔABC is isosceles and ΔBCD is equilateral . ¯¯¯¯¯¯AB=¯¯¯¯¯¯BC and the measure of ∠ABC is half the measure of ∠BAC. what is the measure of ∠ABD ?
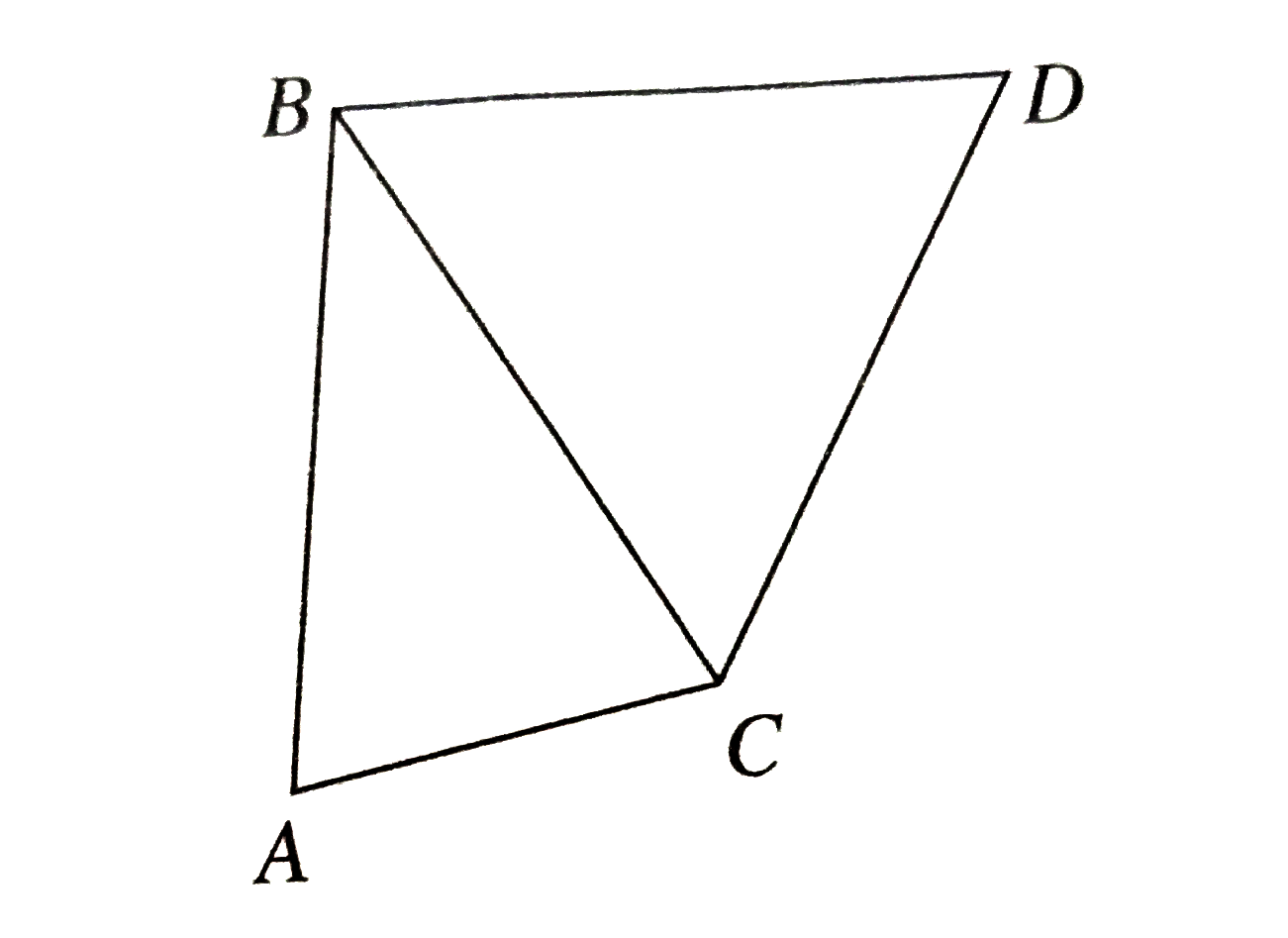 A36∘B60∘C72∘D96∘
A36∘B60∘C72∘D96∘An equilateral triangle has three lines of symmetry, an isosceles triangle will have :
Ano line of symmetryBone line of symmetryCtwo lines of symmetryDThree lines of symmetry
A point 'P' is an arbitrary interior point of an equilateral triangle of side 4. If x, y, z are the distances of 'P' from sides of the triangle then the value of (x+y+z)2 is equal to -
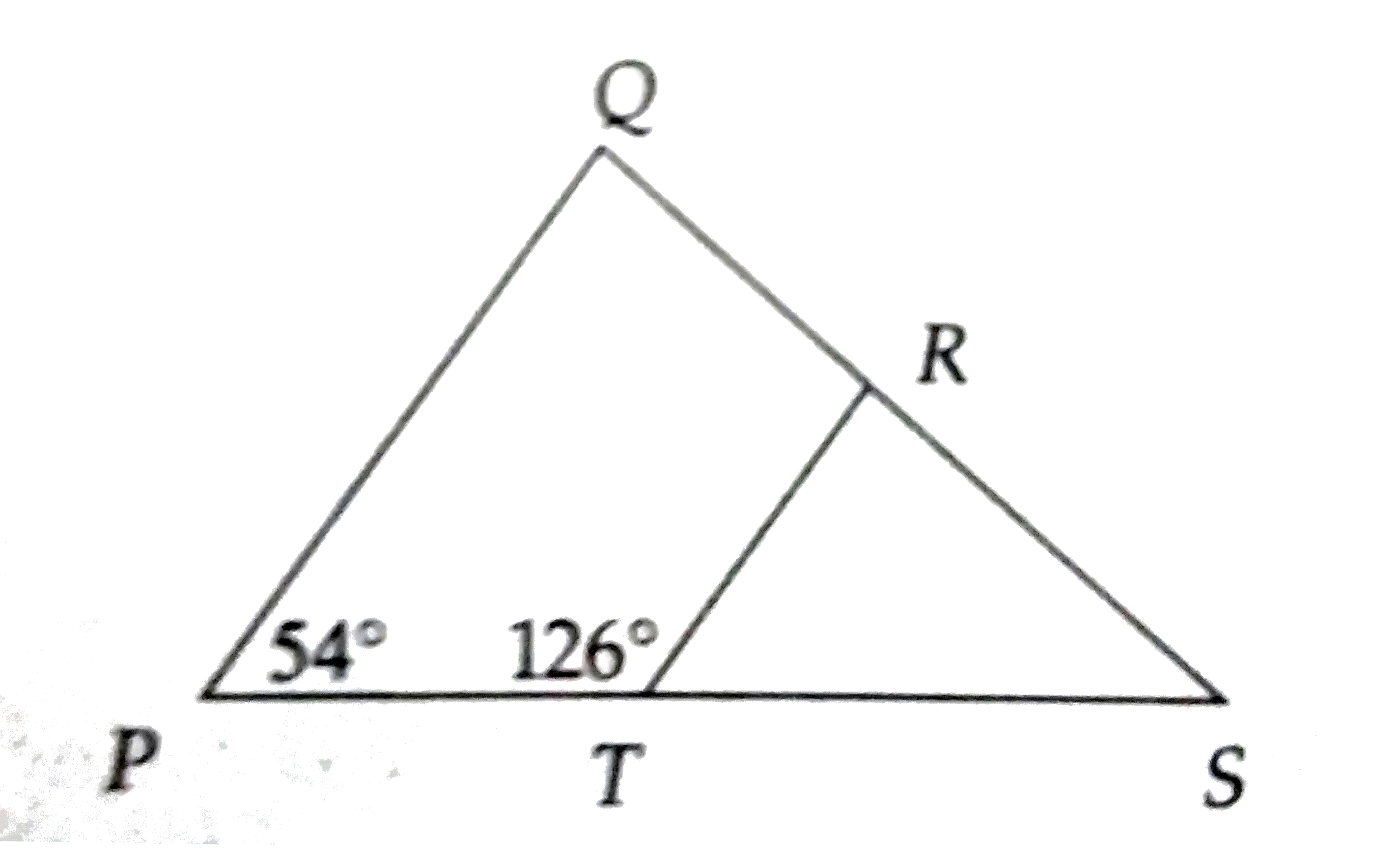
View Solution¯¯¯¯¯¯QR=¯¯¯¯¯RS. If the area of ΔRST is c2, what is the area of ΔQSP ?
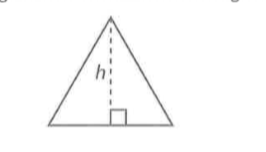
View SolutionEach side of the equilateral triangle shown is 2. What is the height h of the triangle?
View SolutionIf the length of two sides of an isosceles triangle are 3 and 7, what is the perimeter of the triangle?
View SolutionIf each side of an equilateral triangle is tripled then what is the percentage increase in the area of the triangle?
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral ΔPQR and a mass of 2kg is placed at the centroid O of the triangle which is at a distance of √2m from each the verticles of the triangle. Find the force (in newton) acting on the mass of 2 kg.
View Solution