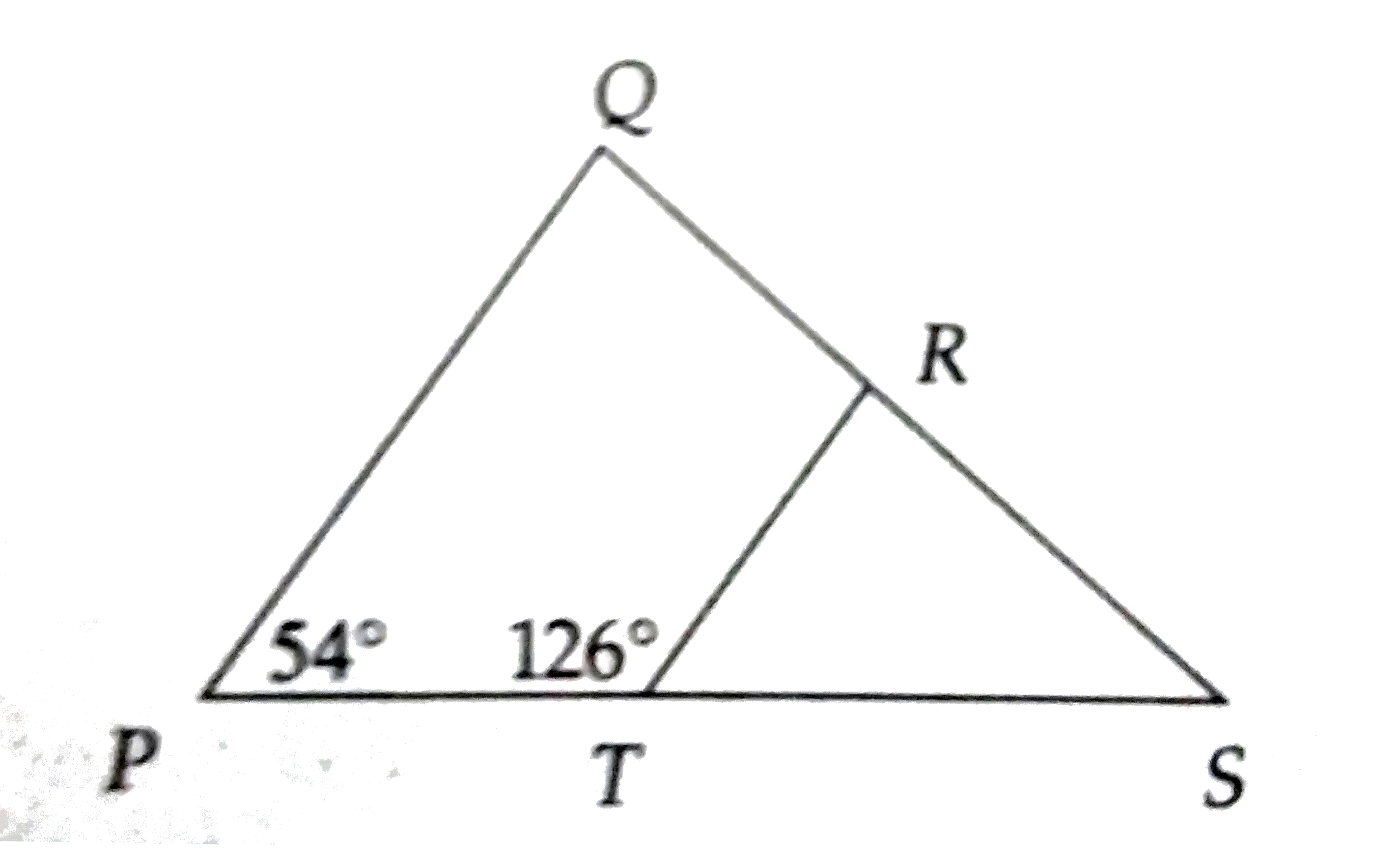
¯¯¯¯¯¯QR=¯¯¯¯¯RS. If the area of ΔRST is c2, what is the area of ΔQSP ?
A
c√2
B
c√3
C
c
D
2c
Video Solution
Text Solution
The correct Answer is:D
You might wonder here how you're supposed to find the area of ΔQSP when you're given no lengths you can for a base or an altitude. The only numbers you have are the angle measures. They must be there for some reason - the makers never provide superfluous information. In fact, because the two angle measures provided add up to 180∘, you know that ¯¯¯¯¯¯PQ and ¯¯¯¯¯¯TR are parallel. And that, in turn you that ΔRST is similar to ΔQSP, because they have the same three angles.
Similar triangles are triangles that have the same shape : Corresponding angles are equal and corresponding sides are proportional. In this case, because it's given that ¯¯¯¯¯¯QR=¯¯¯¯¯RS, you know that ¯¯¯¯¯¯QS is twice ¯¯¯¯¯¯QR and that corresponding sides are in a ratio of 2 : 1. Each side of the larger triangle is twice the length of the corresponding side of the smaller triangle. That doesn't mean, however, that the ratio of the areas is also 2 : 1. In fact, the area ratio is the square of the side ratio, and the larger triangle has four times the area of the smaller triangle.
area of ΔQSP=4× area of ΔRST=4×c2=2c.
|
Topper's Solved these Questions
- PLANE GEOMETRY Book:KAPLANChapter:PLANE GEOMETRY Exercise:PLANE GEOMETRY FOLLOW - UP TEST
Explore 6 Videos
- MISCELLANEOUS TOPICS Book:KAPLANChapter:MISCELLANEOUS TOPICS Exercise:MISCELLANEOUS TOPICS FOLLOW - UP TEST
Explore 12 Videos
- PRACTICE TEST 1 Book:KAPLANChapter:PRACTICE TEST 1 Exercise:PRACTICE TEST
Explore 50 Videos
Similar Questions
Knowledge Check
What is the area of the triangle?
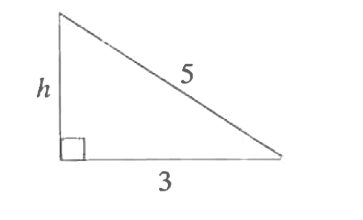 A6B7.5C8D11
A6B7.5C8D11In the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2In the figure, what is the area of ΔABC?
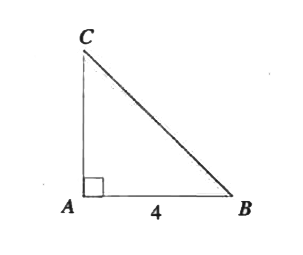 A6B7C8DIt cannot be determined from the information given
A6B7C8DIt cannot be determined from the information given
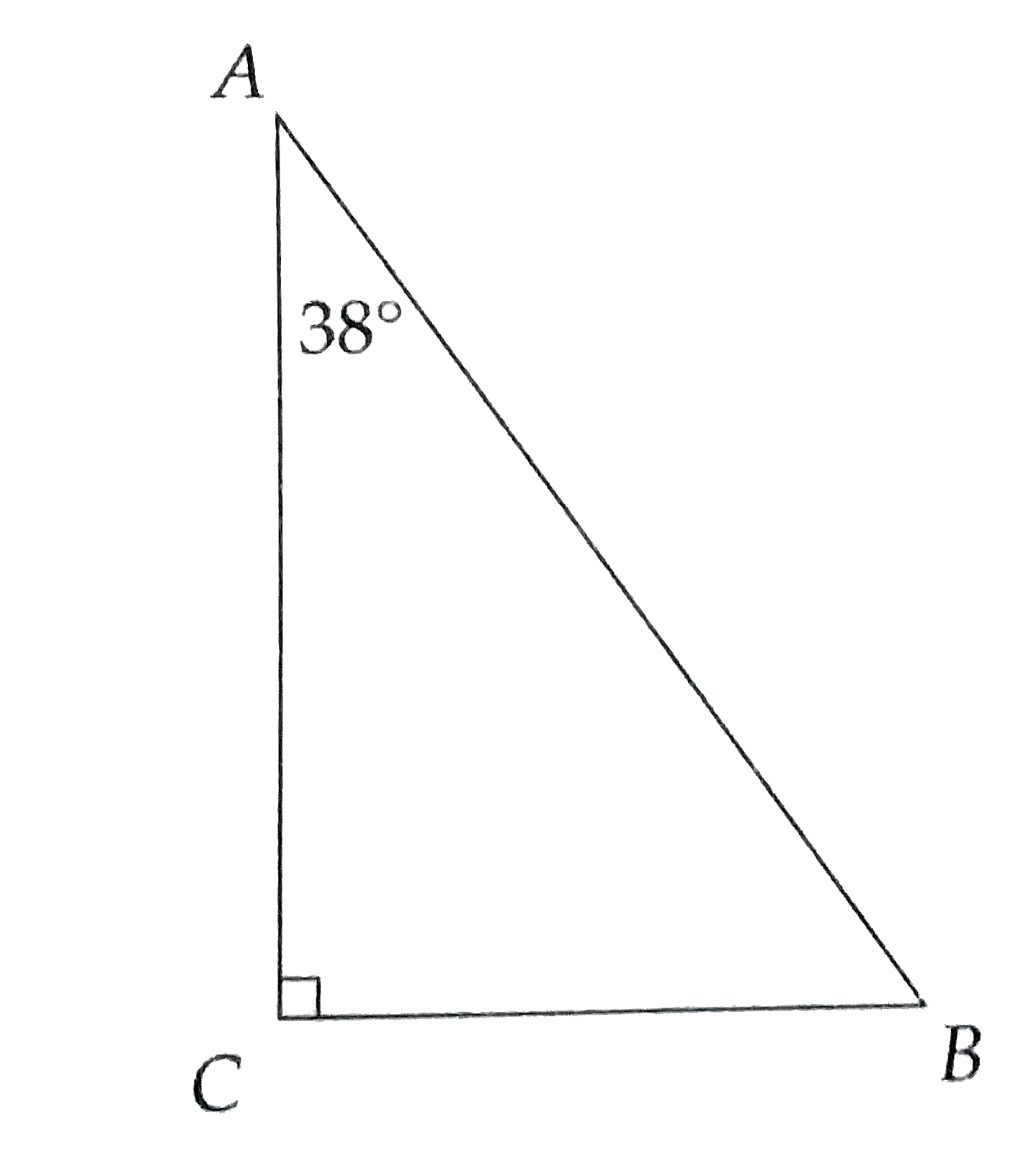
If the area of triangle ABC is 15, what is the length of AC ?
View SolutionIf Δ=a2−(b−c)2,Δ is the area of the ΔABC then tanA= ?
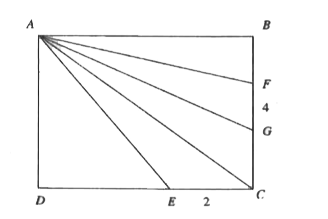
View SolutionIf ABCD is a square and the area of ΔAFG is 10, then what is the area of ΔAEC ?
View Solution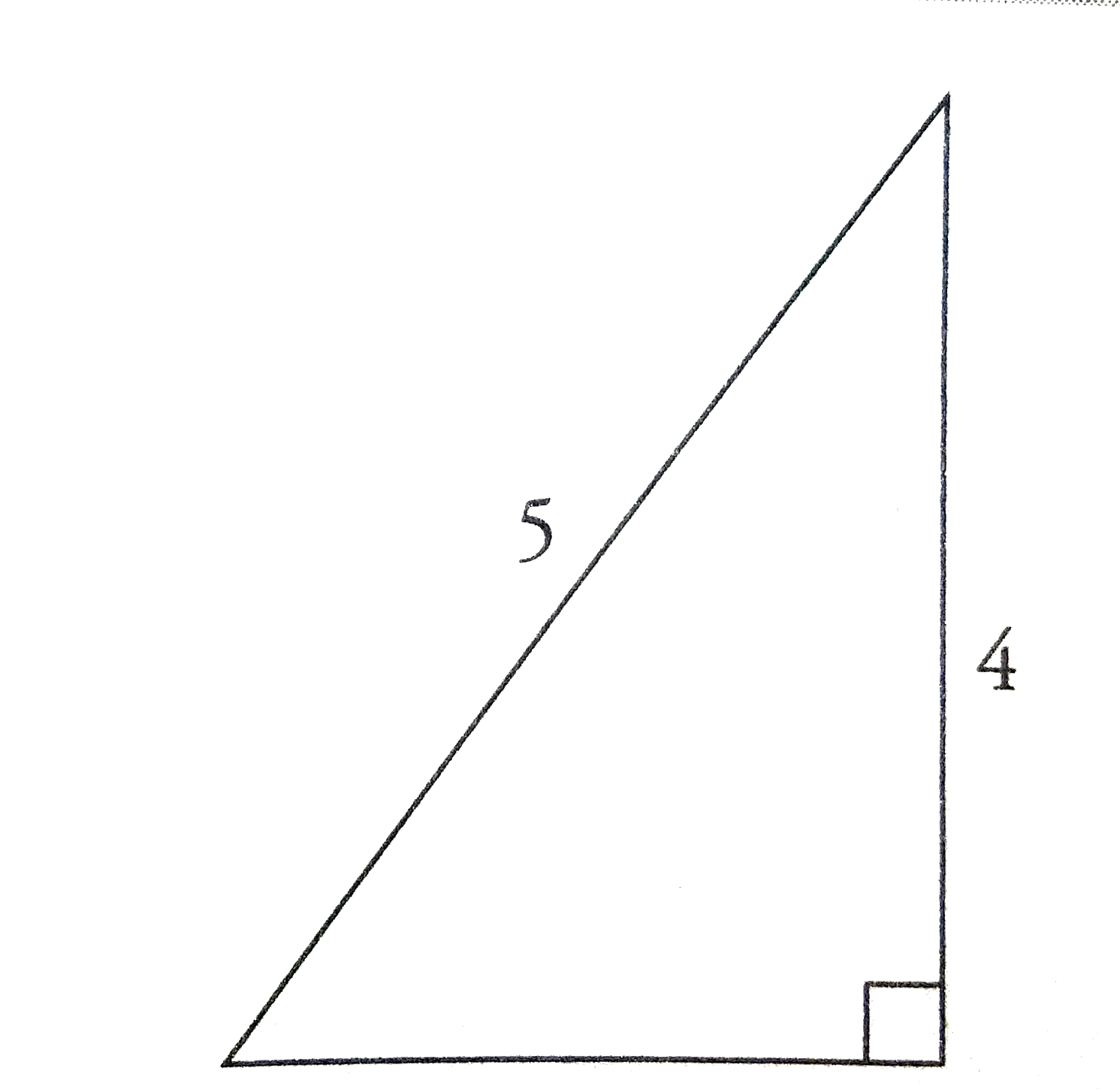
If the area of the triangle above is 6, what is its perimeter?
View Solution
If the perimeter above is 18, what is the area of the triangle?
View Solution