The ratio of ¯¯¯¯¯¯DB to ¯¯¯¯¯¯EF is 4 to 9. If ¯¯¯¯¯¯DF=2, what is the distance from D to the midpont of ¯¯¯¯¯¯EF ?
A
913
B
1213
C
1413
D
1713
Video Solution
Text Solution
The correct Answer is:D
Mark up the figure :
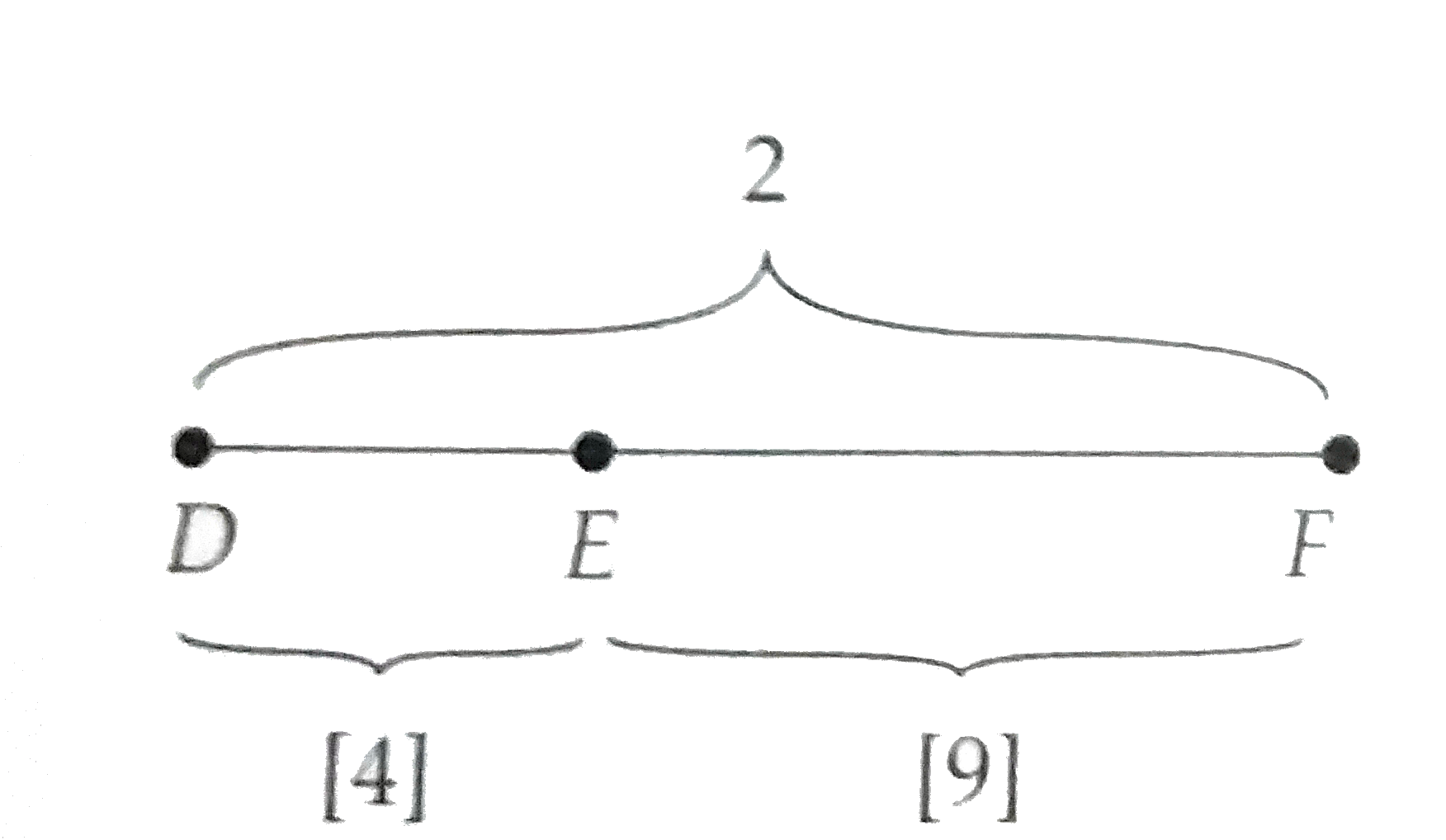
The brackets around the 4 and the 9 are meant to show that they're proportions, not actual lengths. Since the ratio of ¯¯¯¯¯¯DE to ¯¯¯¯¯¯EF is 4 9, you can say that 4 parts out of 13 are in ¯¯¯¯¯¯DE and 9 parts out of 13 are in ¯¯¯¯¯¯EF.
Because the whole length ¯¯¯¯¯¯DF=2,¯¯¯¯¯¯DE=413×2=813
and ¯¯¯¯¯¯EF=913×2=1813. The midpoint of ¯¯¯¯¯¯EF divides it in half, so each half length is half of 1813, which is 913. The length you're looking for is 813+913=1713.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
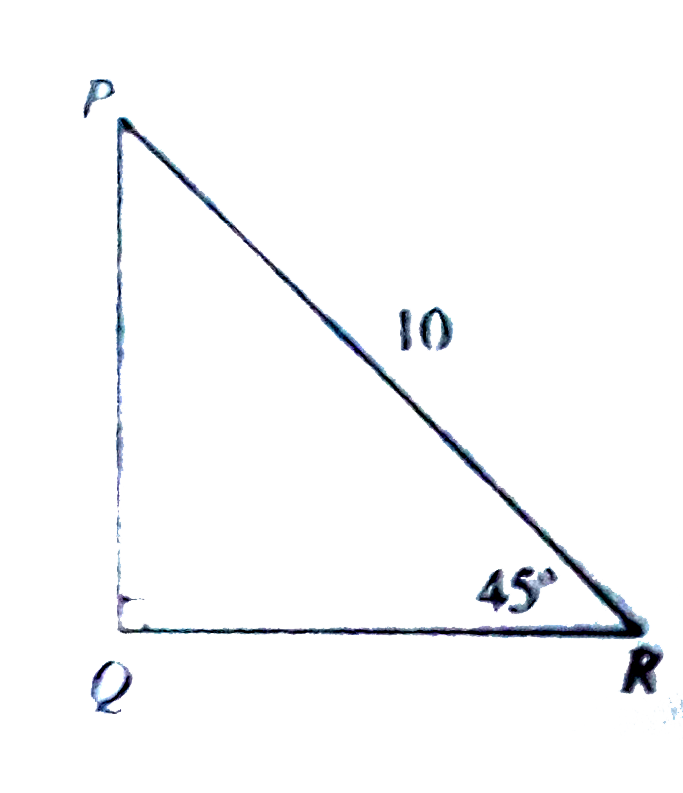
What is the length of ¯¯¯¯¯¯QR ?A5B5√22C10√2D5√2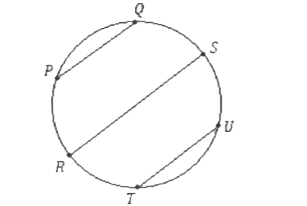
In the circle above with diameter d, chords ¯¯¯¯¯¯PQand¯¯¯¯¯¯TU are parallel to diameter ¯¯¯¯¯RS. If ¯¯¯¯¯¯PQand¯¯¯¯¯¯TU are each 34 of the length of ¯¯¯¯¯RS, what is the distance between chords ¯¯¯¯¯¯PQand¯¯¯¯¯¯TU in terms of d?Ad√78Bd√74Cπd4D3πd4In the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
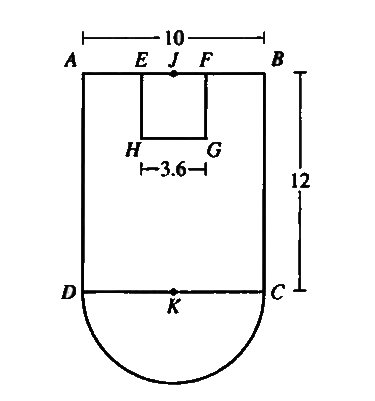
The length of ¯¯¯¯¯¯EH is what precent of the length of ¯¯¯¯¯¯AD?A0.156B0.3C0.36D0.432
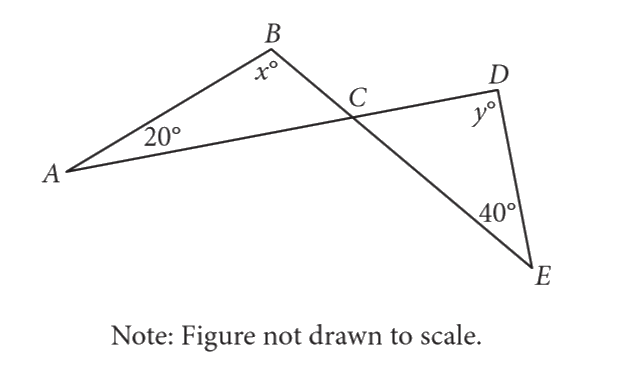
In the figure above, ¯¯¯¯¯¯AD intersects ¯¯¯¯¯¯BE at C. If x = 100, what is the value of y ?
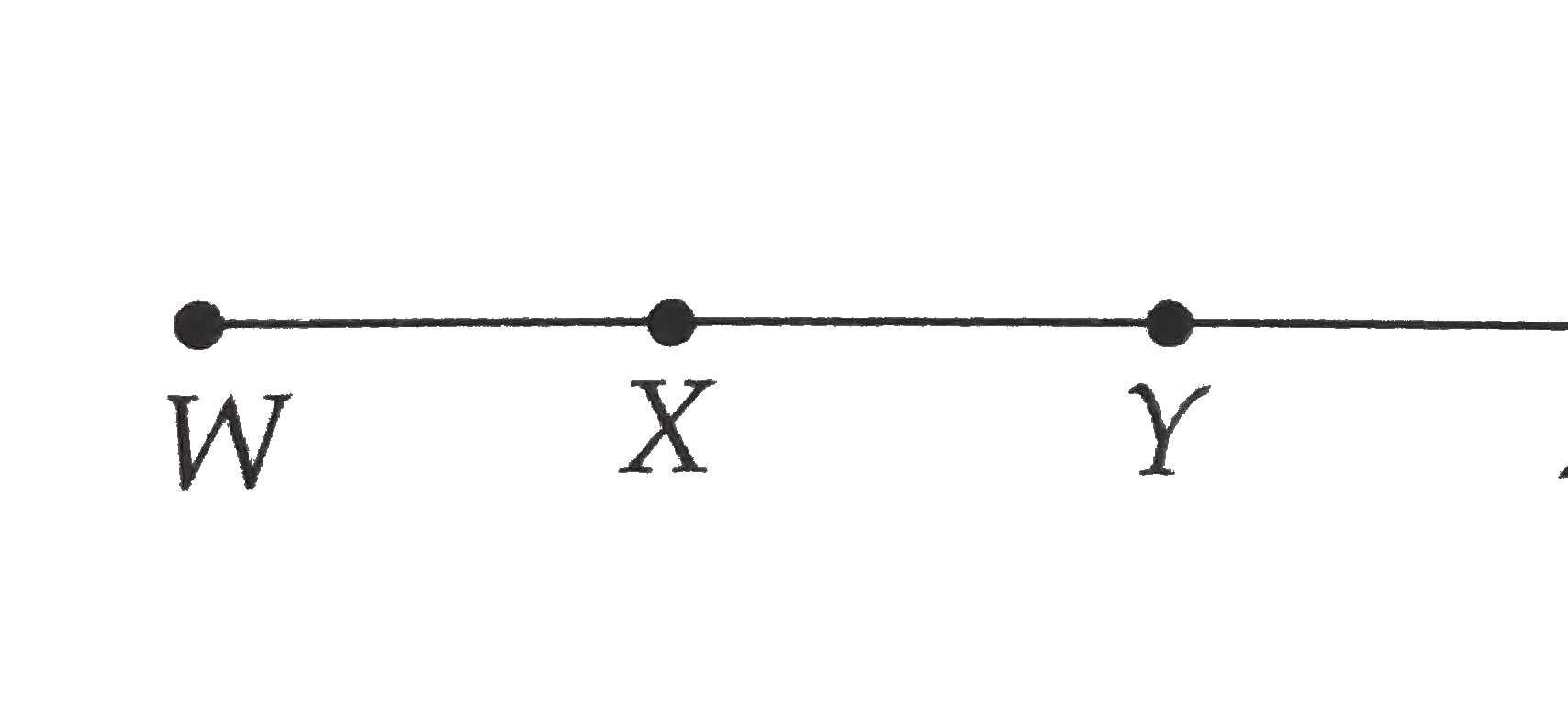
View SolutionThe length of ¯¯¯¯¯¯¯WZ is 3a+15, and the length of ¯¯¯¯¯¯¯WX is 7a+5. If Y is the midpoint of ¯¯¯¯¯¯XZ, what is the length of ¯¯¯¯¯¯¯WY ?
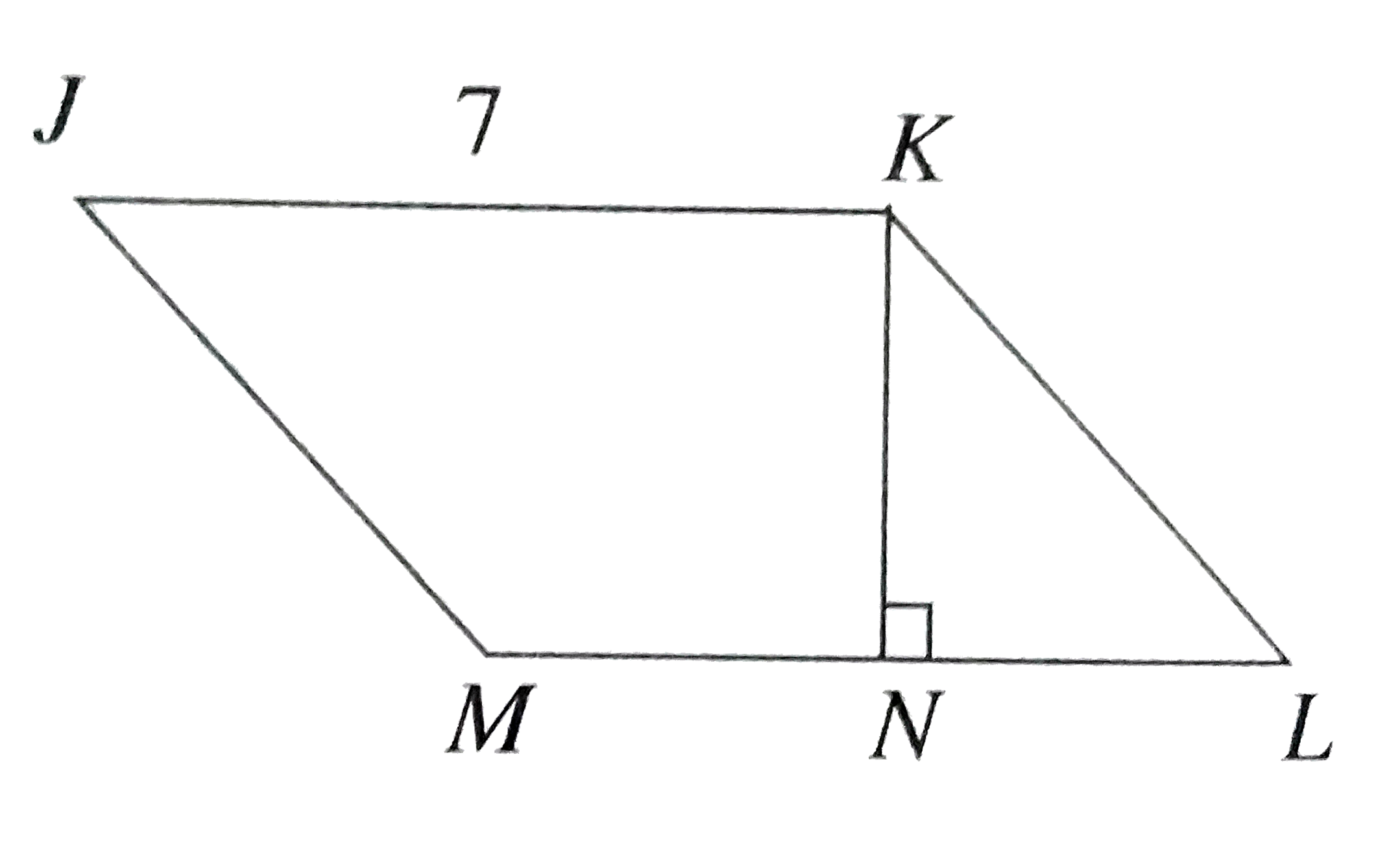
View SolutionThe area of parallelogram JKLM is 28 ¯¯¯¯¯¯JK=7. If ¯¯¯¯¯¯¯KN is perpendicular to ¯¯¯¯¯¯¯ML and if N is the midpoint of ¯¯¯¯¯¯¯ML, what is the perimeter of JKLM ?
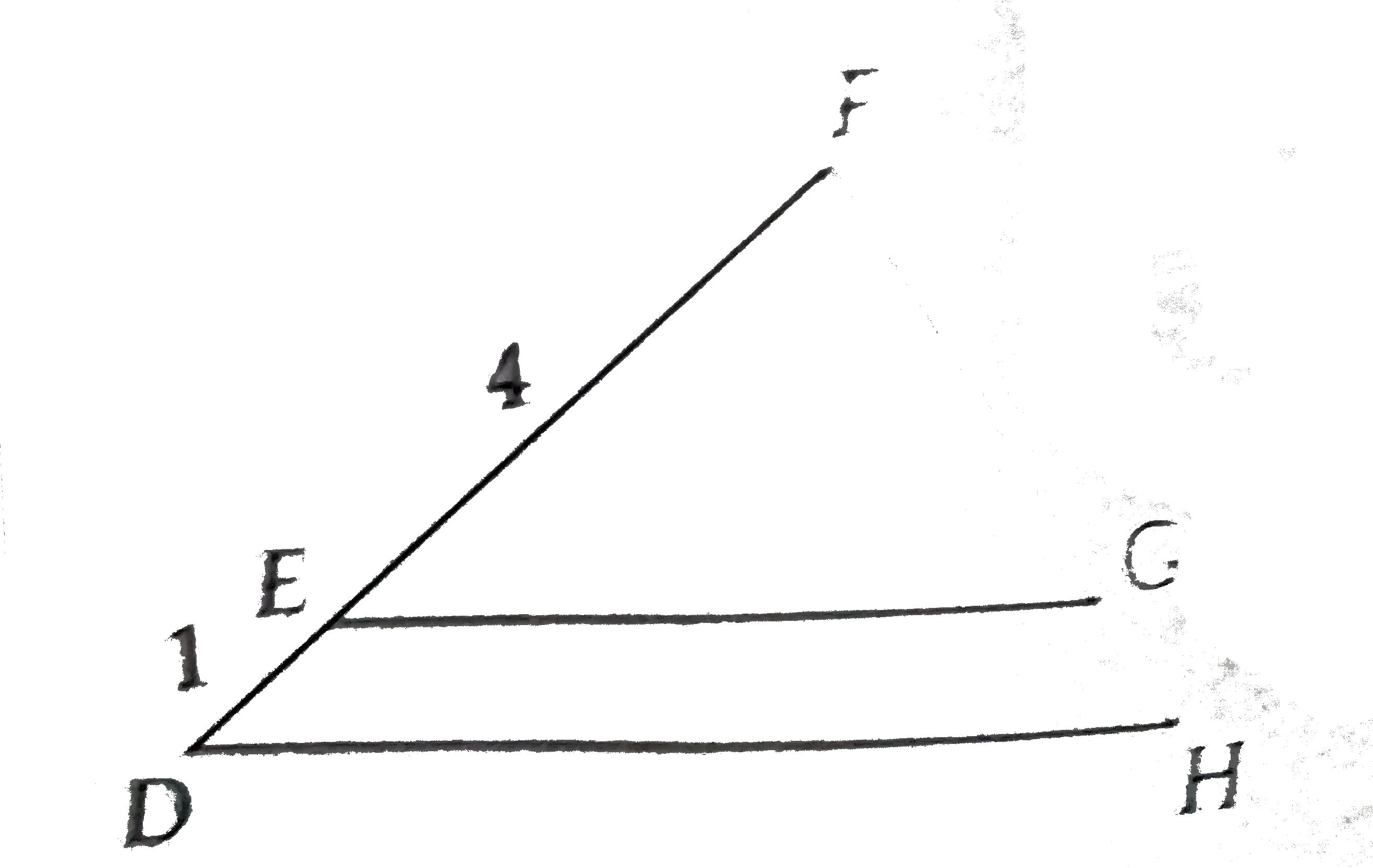
View Solution¯¯¯¯¯¯EG∣∣¯¯¯¯¯¯¯DH, and the length of segments ¯¯¯¯¯¯DE and ¯¯¯¯¯¯EF are as marked. If the area of ΔEFG is a, what is the area of ΔDFH in terms of a ?
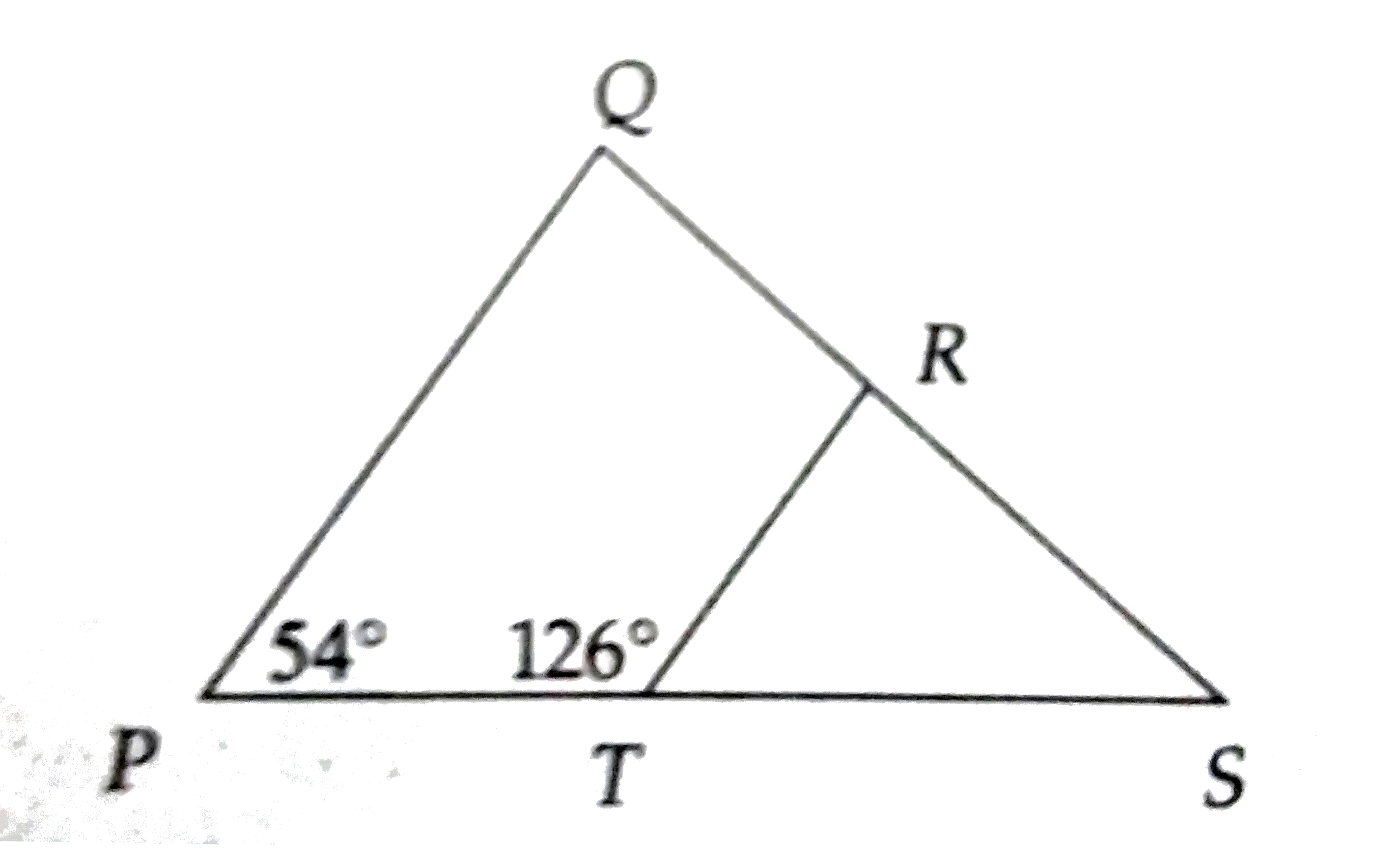
View Solution¯¯¯¯¯¯QR=¯¯¯¯¯RS. If the area of ΔRST is c2, what is the area of ΔQSP ?
View Solution