Three equal masses of 1 kg each are placed at the vertices of an equilateral ΔPQR and a mass of 2kg is placed at the centroid O of the triangle which is at a distance of √2m from each the verticles of the triangle. Find the force (in newton) acting on the mass of 2 kg.
To solve the problem of finding the force acting on the mass of 2 kg placed at the centroid O of the equilateral triangle formed by three 1 kg masses at vertices P, Q, and R, we can follow these steps:
Step 1: Understand the setup
We have three equal masses (1 kg each) located at the vertices of an equilateral triangle PQR. The centroid O of this triangle has a mass of 2 kg placed at it. The distance from each vertex to the centroid is given as √2 m.
Step 2: Calculate the gravitational force exerted by each mass on the mass at the centroid
The gravitational force F exerted by a mass m1 on another mass m2 separated by a distance r is given by the formula:
F=G⋅m1⋅m2r2
In our case:
- m1=1 kg (mass at the vertex)
- m2=2 kg (mass at the centroid)
- r=√2 m
Substituting these values into the formula:
F=G⋅1⋅2(√2)2=G⋅22=G
Thus, the gravitational force exerted by each 1 kg mass on the 2 kg mass at the centroid is G.
Step 3: Determine the direction of the forces
The forces exerted by the three 1 kg masses on the 2 kg mass are directed towards each of the vertices (P, Q, and R). Since the triangle is equilateral, the angles between the lines of force are 120∘.
Step 4: Use vector addition to find the resultant force
The three forces F1,F2, and F3 acting on the mass at the centroid can be represented as vectors. Since the magnitudes of these forces are equal and the angles between them are 120∘, we can use the principle of vector addition.
Using the concept of symmetry in an equilateral triangle, we can conclude that the resultant force from the three equal forces will be zero. This is because the forces will cancel each other out due to their equal magnitudes and symmetrical arrangement.
Conclusion
The net force acting on the mass of 2 kg at the centroid O is:
Net Force=0N
We have three equal masses (1 kg each) located at the vertices of an equilateral triangle PQR. The centroid O of this triangle has a mass of 2 kg placed at it. The distance from each vertex to the centroid is given as √2 m.
The gravitational force F exerted by a mass m1 on another mass m2 separated by a distance r is given by the formula:
F=G⋅m1⋅m2r2
In our case:
- m1=1 kg (mass at the vertex)
- m2=2 kg (mass at the centroid)
- r=√2 m
F=G⋅1⋅2(√2)2=G⋅22=G
Thus, the gravitational force exerted by each 1 kg mass on the 2 kg mass at the centroid is G.
The forces exerted by the three 1 kg masses on the 2 kg mass are directed towards each of the vertices (P, Q, and R). Since the triangle is equilateral, the angles between the lines of force are 120∘.
The three forces F1,F2, and F3 acting on the mass at the centroid can be represented as vectors. Since the magnitudes of these forces are equal and the angles between them are 120∘, we can use the principle of vector addition.
The net force acting on the mass of 2 kg at the centroid O is:
Net Force=0N
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Solved Examples
16 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples
8 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Three equal masses of 2kg each are placed at the vertices of an equilateral triangle and a mass of 4 kg is placed at the centroid of the triangle which is at a distance of √2 m from each of the vertices of the triangle. The force, (in newton) acting on the mass of 4 kg is
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle and other particle of mass 2kg is placed on centroid of triangle which is at a distance of √2 m from each of the vertices of the triangle .The force in newton , acting on the particle of mass 2 kg is
View Solution
Knowledge Check
Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
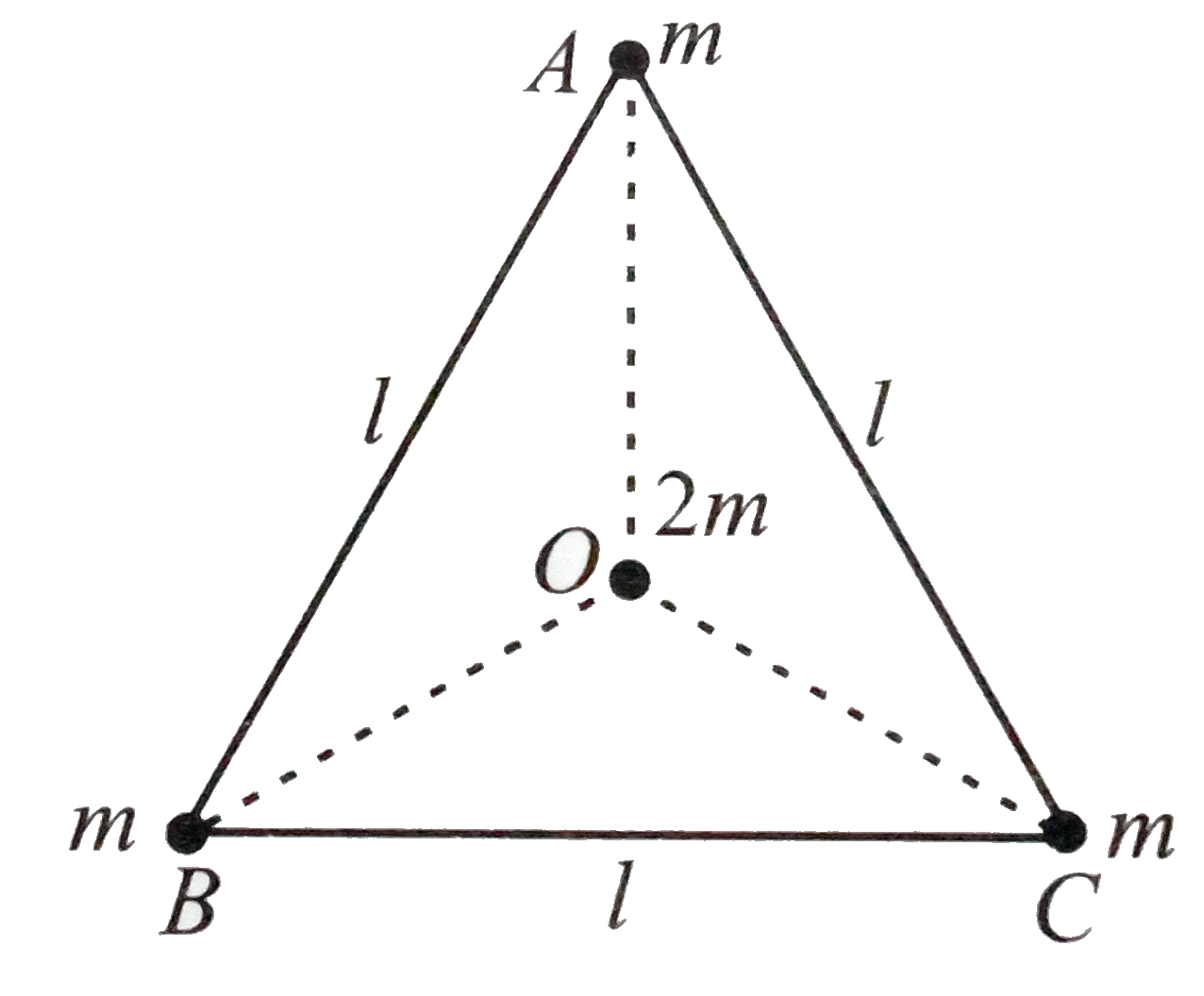 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2
Three equal charges, each +q are placed on the corners of an equilatreal triangel . The electric field intensity at the centroid of the triangle is
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
View SolutionThree equal masses of mkg each are fixed at the vertices of an equilateral triangle ABC.
a. What is the force acting on a mass 2m placed at the centroid G of the triangle?
b. What is the force if the mass at the vertex A is doubled? Take AG=BG=CG=1m
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)
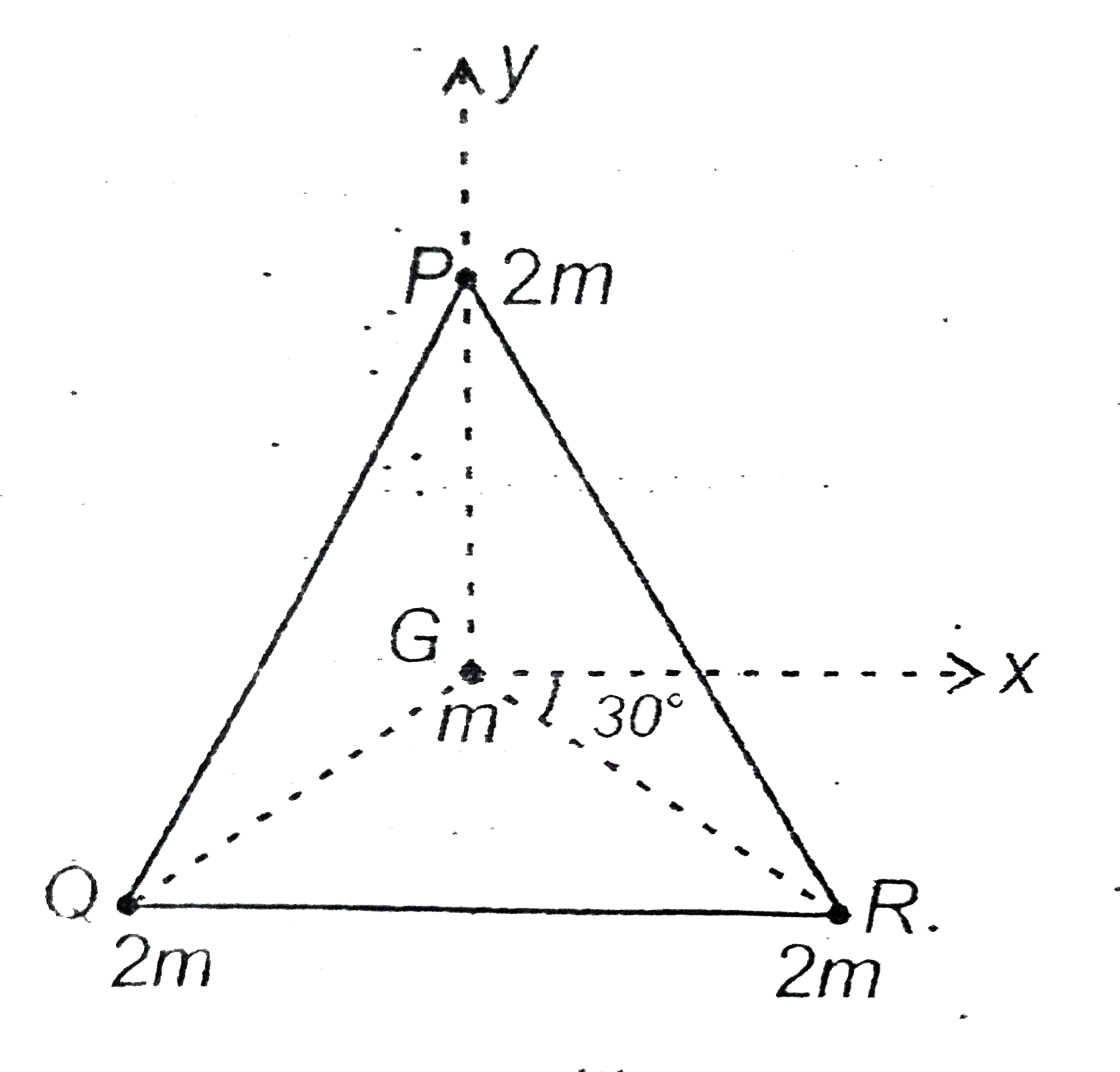
View SolutionThree equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m
View SolutionThree masses 3, 4 and 5 kg are placed at the centre of an equiliteral triangle of 1 m sides. Locate its centre of mass.
View Solution
