A ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept on a smooth, horizontal surface as shown in figure. If impulse between ball and wedge during collision is J. Then make two equations which relate J with velocity components of wedge and ball. Also find impulse on wedges from ground during impact.
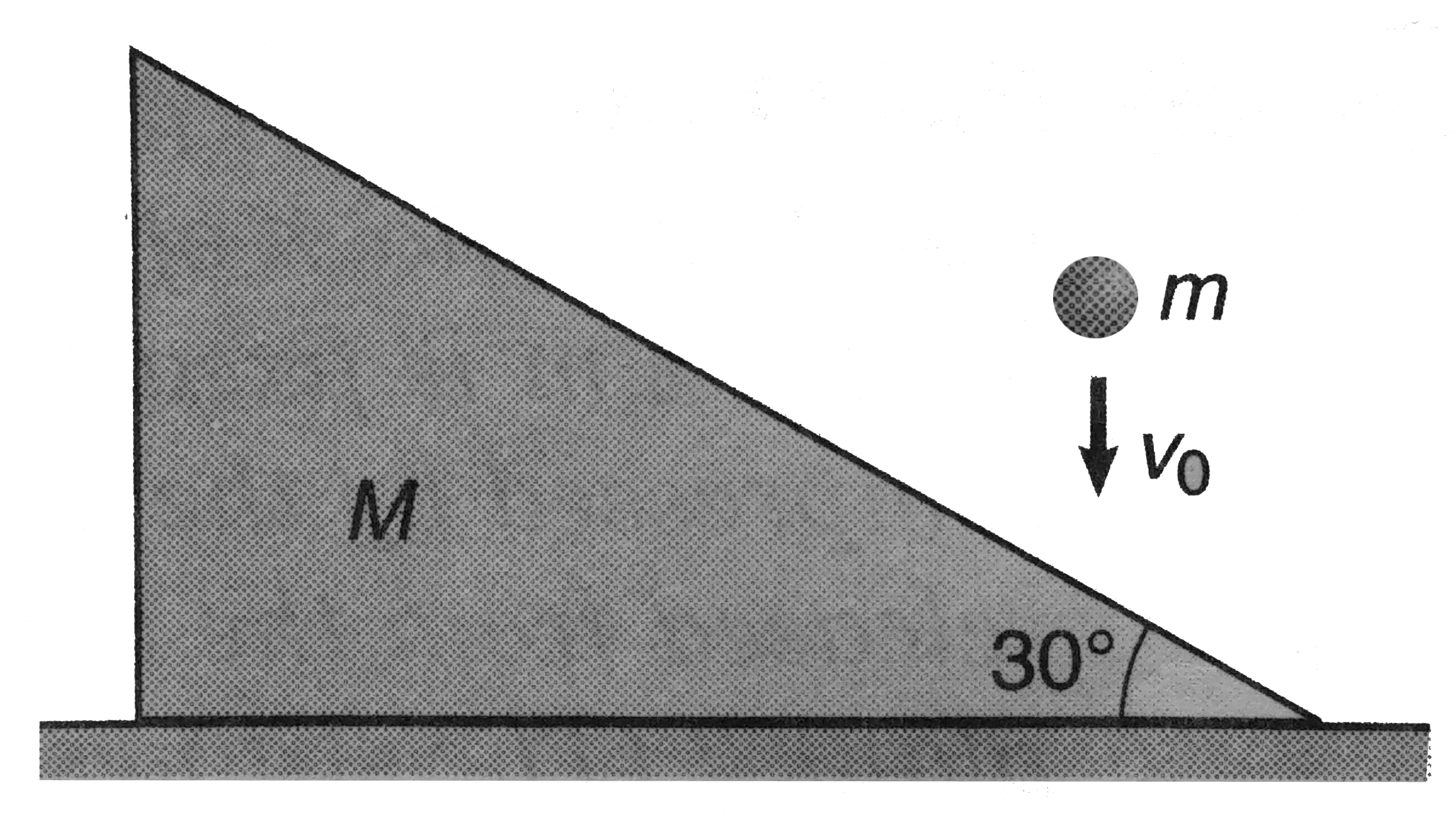
The correct Answer is:v1=1√3ms−1,v2=2√3ms−1
Let v= velocity of the ball after collision along the normal
J= impulse on ball
=v−(−2cos30∘)=v+√3
Impulse on wedge Jsin30∘=mv1=2v1
⇒v=4v1−√3 …..(i)
e=−(v2−v1u2−u1)⇒12=(v+v12)2cos30∘
⇒v=√32−v12 ....(ii)
Solving we get v1−1√3m/s
For th eball velocity along incline remains constant.
∴v'=2sin30∘=1m/s
∴ Final velocity of ball =
⎷12+(1√3)2=−2√3m/s
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-V A
Explore 20 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-V B
Explore 19 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-IV A
Explore 32 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
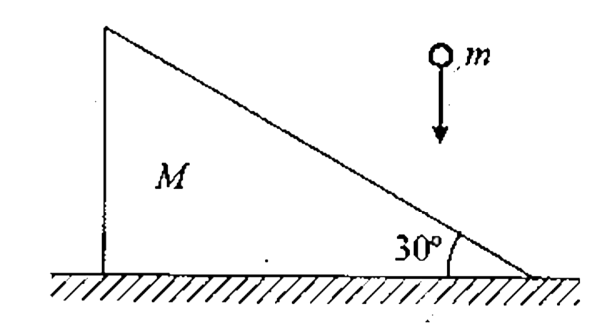
A ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept o a smooth, horizontal surface as shown in figure. The coefficient of resitution between the ball and the wege is e=1/2. Find the velocity of the wedge is e=1/2. find the velocity of the wedge and the ball immediately after collison.
View SolutionA particle of mass m strikes normally to a stationary wedge of mass 5m kept on the smooth horizontal surface as shown.If the particle sticks to the wedge then loss in kinetic energy of the system during collision is?
View Solution
Knowledge Check
A ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is
 A(a) 6.25NsB(b) 1.76NsC(c) 7.8NsD(d) 2.2Ns
A(a) 6.25NsB(b) 1.76NsC(c) 7.8NsD(d) 2.2NsA small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. It h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
 AMhcotθM+mB(b) mhcotθM+mC(c) MhcosecθM+mD(d) mhcosecθM+m
AMhcotθM+mB(b) mhcotθM+mC(c) MhcosecθM+mD(d) mhcosecθM+m
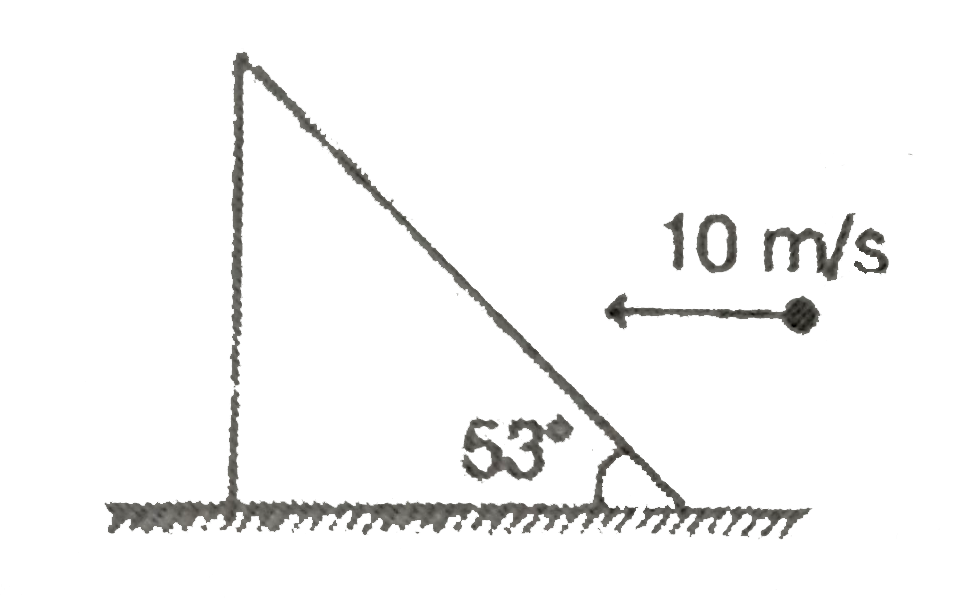
A ball mass 2 kg moving horizontally with velocity 10 m/s hits a wedge of mass 5 kg placed on a horizontal surface as shown in the figure. Just after collision klvelocity of wedge is 3.2 m/s. There is no friction at any contact surface. Then (take sin 30∘=3/5)
View SolutionA small particle of mass m=2kg moving with constant horizontal velocity u=10m/s strikes a wedge shaped block of mass M=4kg placed on smooth horizontal surface on its inclined surface as shown in figure. After collision particle starts moving up the inclined plane. Calculate the velocity of wedge immediately after collision.
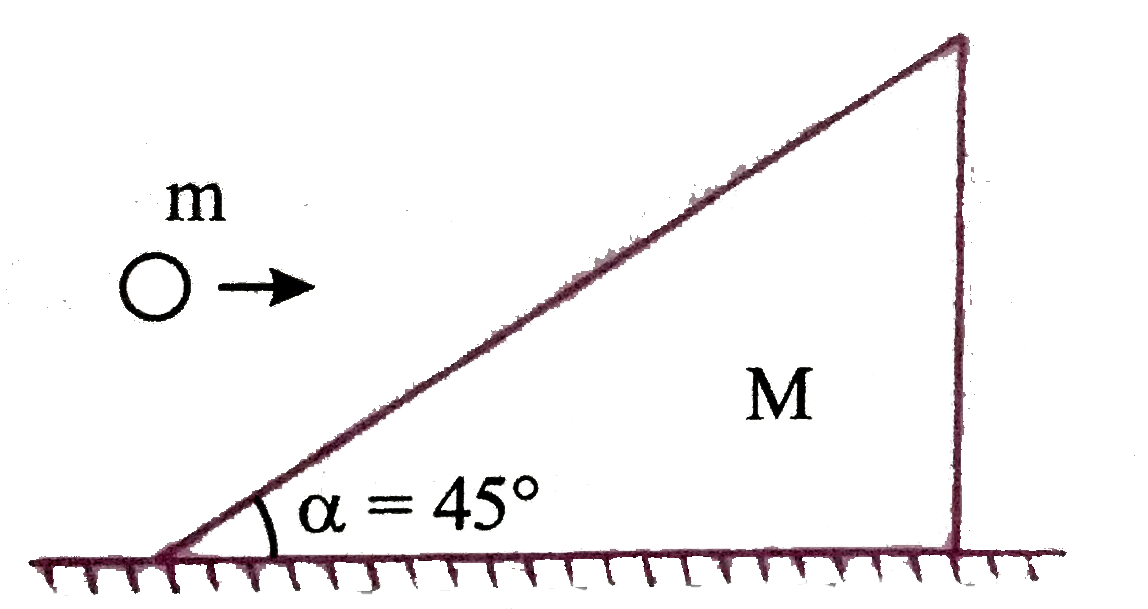
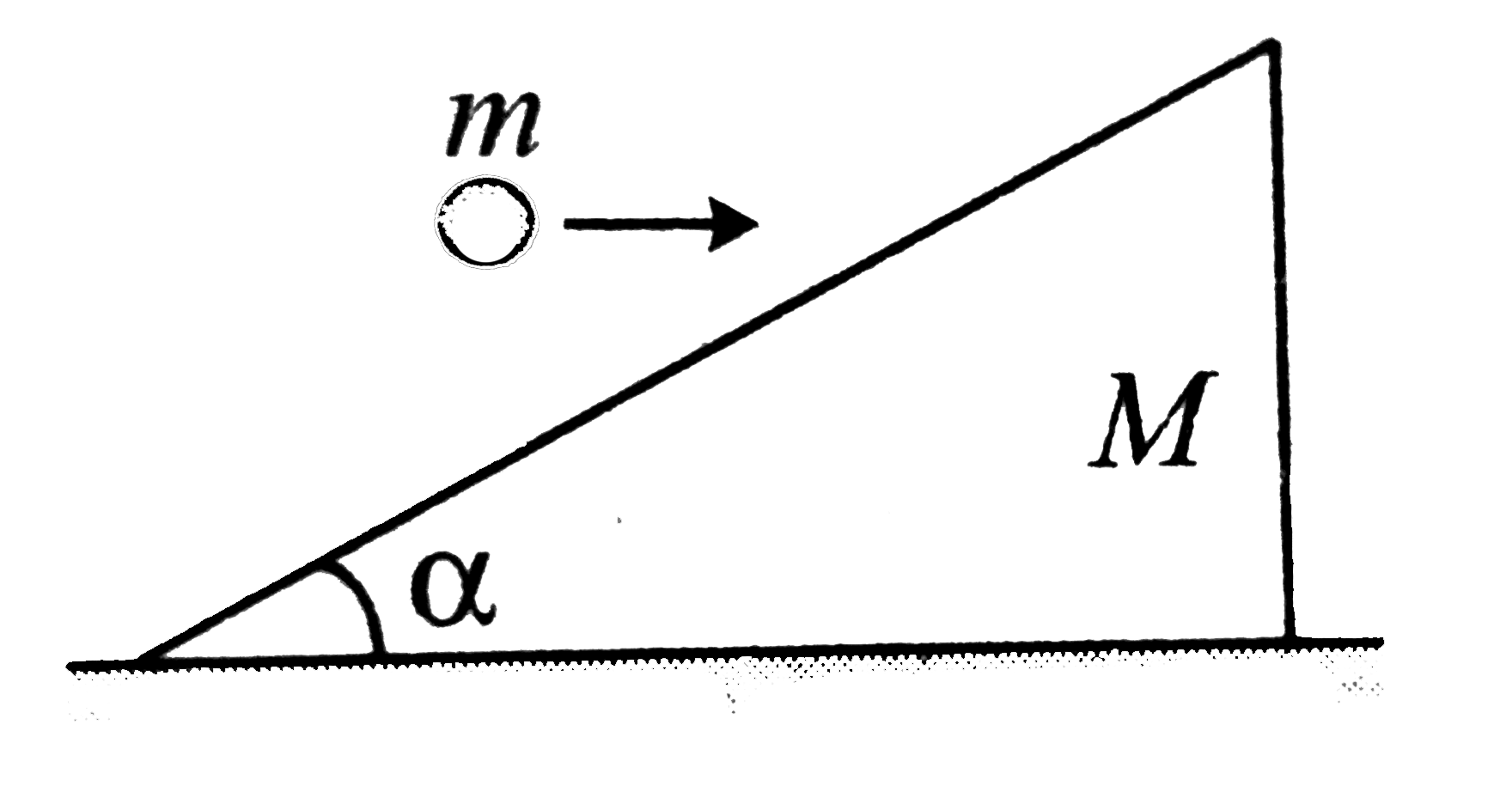
View SolutionA ball of mass m moving with constant horizontal velocity u strikes a stationary wedge of mass M on its inclined surface as shown in the figure. After collision, the ball starts moving up the inclined plane. The wedge is placed on frictionless horizontal surface.
a. Calculate the velocity of wedge immediately after collision.
b. Calculate the maximum height the ball can ascend on the wedge.
View SolutionA ball of mass m moving horizotally which velocity u hits a wedge of mass M. The wedge is situated on a smooth horizontal source. If after striking with wedge the ball starts moving in vertical direction and the wedge starts moving in horizotal plane. calculate
a. the velocity of wedge V.
b. the velocity (v) at which the ball moves in vertical direction.
c. the impulse imparted by the ball on the wedge.
d. the coefficient of restitution e=?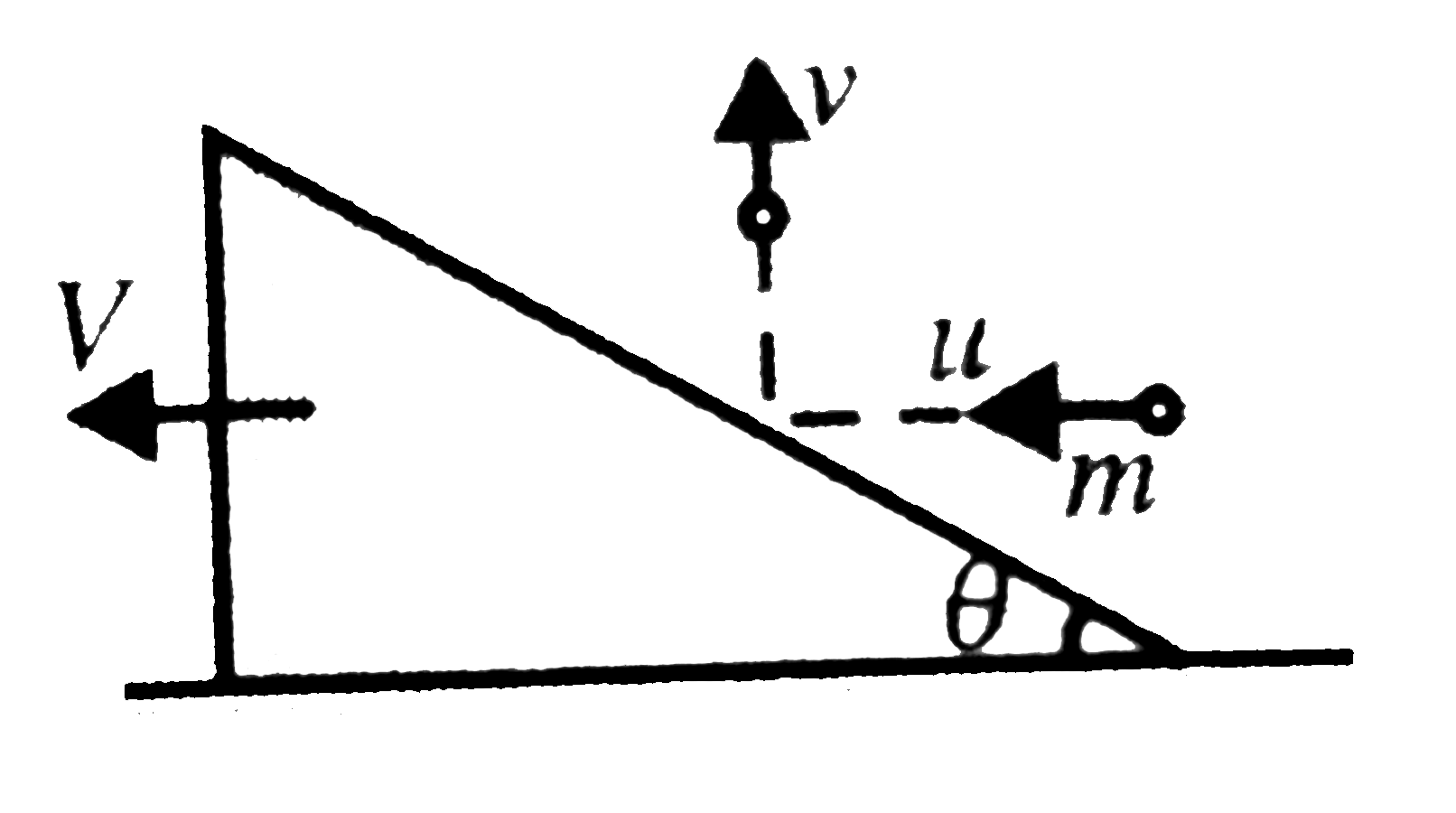
View SolutionA 250 g ball moving horizontally with velocity 10.0m/s strikes inclined surface of a 720g smooth wedge as shown in the figure. The wedge is placed at rest on a frictionless horizontal ground. If the coefficient of restitution is 0.8, calculate the velocity of the wedge after the impact.

View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
View Solution

