A 250 g ball moving horizontally with velocity 10.0m/s strikes inclined surface of a 720g smooth wedge as shown in the figure. The wedge is placed at rest on a frictionless horizontal ground. If the coefficient of restitution is 0.8, calculate the velocity of the wedge after the impact.

Let us consider the ball as the body A and the wedge as the body B. Before collision let velocity of ball is u^a after the impact, the ball bounces with velocity vA and the wedge advances in horizontal direction with velocity vB. These velocities and their t and n-components are immediately before and after the impact are shown in the following figures.

Component along t-axis The ball is free to move before and after the impact, therefore its t-component of momentum conserved. hence, t-component of velocities of the ball remains unchanged.
vAt=UAt=10cos37.=8m/s ...(i)
Momentum Conservation In the horizontal direction, there is no extrnal force on both the bodies. Therefore horizontal component of total momentum of both the bodies remain conserved. mAuA=mA(vAtcos37.−vAncos53.)+mBvB
0.25×10=0.25(8×45−3vAn5)+0.72vB
Coefficient of restitution Concept of coefficient of restitution e is applicable only for the n-component velocities.
vBn−vAn=e(uAn−UBn)→3vB5−vAn=0.8(6−0) ...(iii)
From equations (i), (ii) and (iii), we obtain vB=2.0m/s
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
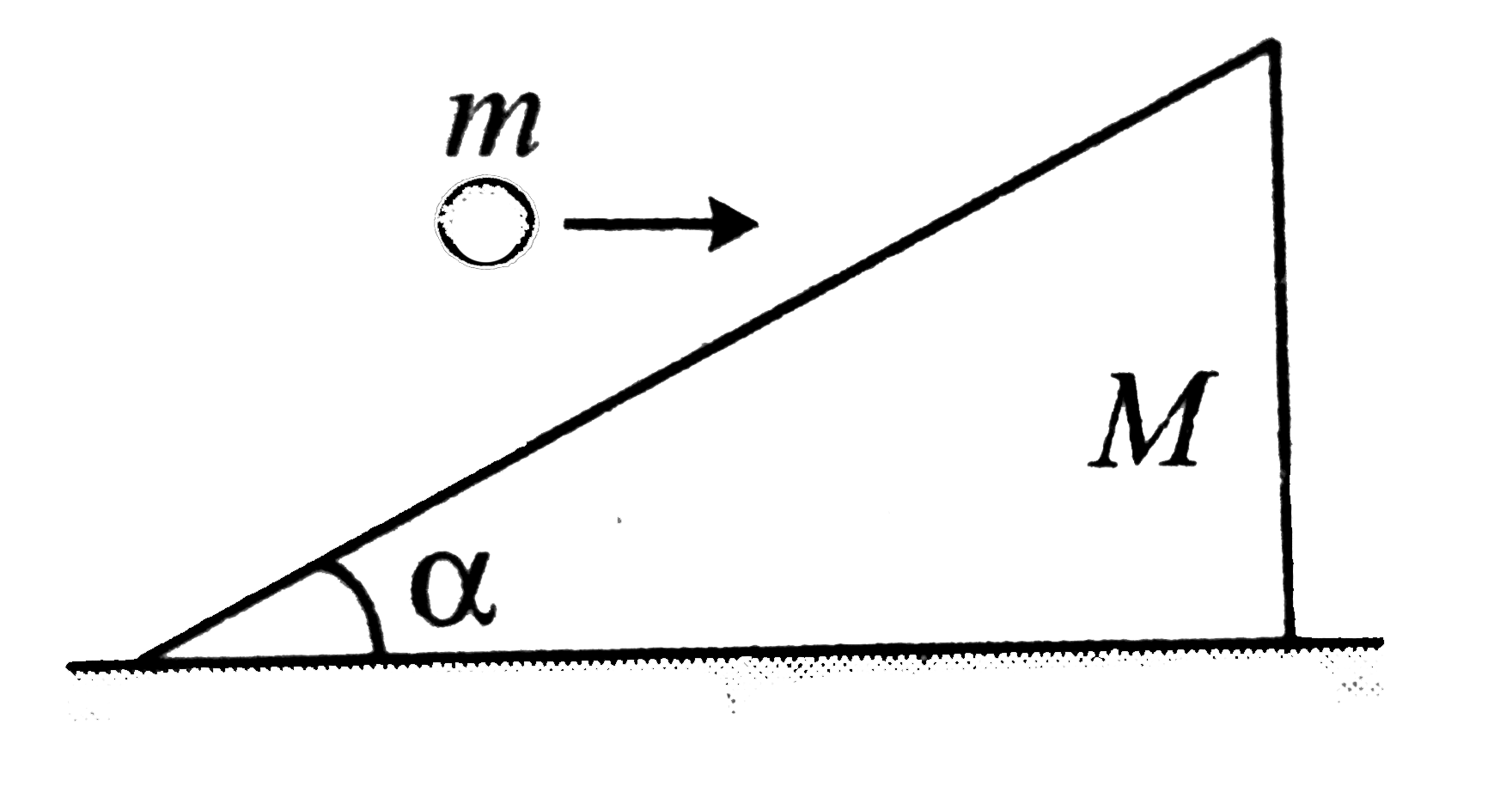
A ball of mass m moving with constant horizontal velocity u strikes a stationary wedge of mass M on its inclined surface as shown in the figure. After collision, the ball starts moving up the inclined plane. The wedge is placed on frictionless horizontal surface.
a. Calculate the velocity of wedge immediately after collision.
b. Calculate the maximum height the ball can ascend on the wedge.
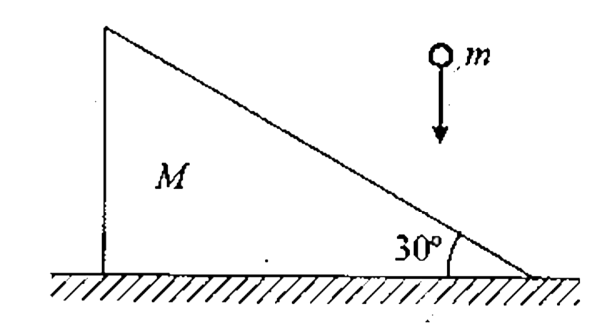
View SolutionA ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept o a smooth, horizontal surface as shown in figure. The coefficient of resitution between the ball and the wege is e=1/2. Find the velocity of the wedge is e=1/2. find the velocity of the wedge and the ball immediately after collison.
View Solution
Knowledge Check
A block of mass 2kg slides down the face of a smooth 45∘ wedge of mass 9kg as shown in the figure. The wedge is placed on a frictionless horizontal surface. Determine the acceleration of the wedge.
 A2ms−2B11√2ms−2C1ms−2Dnone of these
A2ms−2B11√2ms−2C1ms−2Dnone of theseThe air of density ρ and moving with a velocity v strikes perpendicular the inclined surface of area A and of a wedge kept on a horizontal surface. The mass of the wedge is m. Assuming the collisions to be perfectly inelastic, the minimum value of the coefficient of friction between the wedge and the ground so that the wedge does not move is (Assume mass of particles of air is negligible)
 AρAv2sinθmg+ρAv2cosθBtanθCρAv2mgtanθDρAv2mg+ρAv2cosθ
AρAv2sinθmg+ρAv2cosθBtanθCρAv2mgtanθDρAv2mg+ρAv2cosθA small block of mass m is kept on the inclined surface of a wedge of mass M. The inclined surface of the wedge makes an angle θ with the horizontal. The wedge is kept on a frictionless rigid horizontal floor. You can neglect friction between the block and the wedge also. An external agent applies a horizontal force F on the wedge.
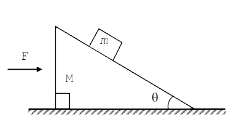
The value of the force F so that the wedge remains at rest is F1. Which of the options is incorrect?AF1 is less than mg sin θBF1 is less then mg cos θCF1 does not depend on MDIt is not possible to keep the wedge at rest
A small ball moving with a velocity 10m/s,horizontally (as shown in figure) strikes a rough horizontal surface having μ=0.5 .If the coefficient of restitution is e=0.4.Horizontal component of velocity of ball after Ist impact will be?(g=10m/s2)
View SolutionA smooth wedge of mass M is kept at rest on a smooth horizontal surface . Inclined face of the wedge make an angle θ with the horizontal . A particle of mass m collides normal to inclined face of wedge . If speed of the particle just before collision is u and coefficient of restitution is e then find velocity of wedge after collision .
View SolutionA small particle of mass m=2kg moving with constant horizontal velocity u=10m/s strikes a wedge shaped block of mass M=4kg placed on smooth horizontal surface on its inclined surface as shown in figure. After collision particle starts moving up the inclined plane. Calculate the velocity of wedge immediately after collision.
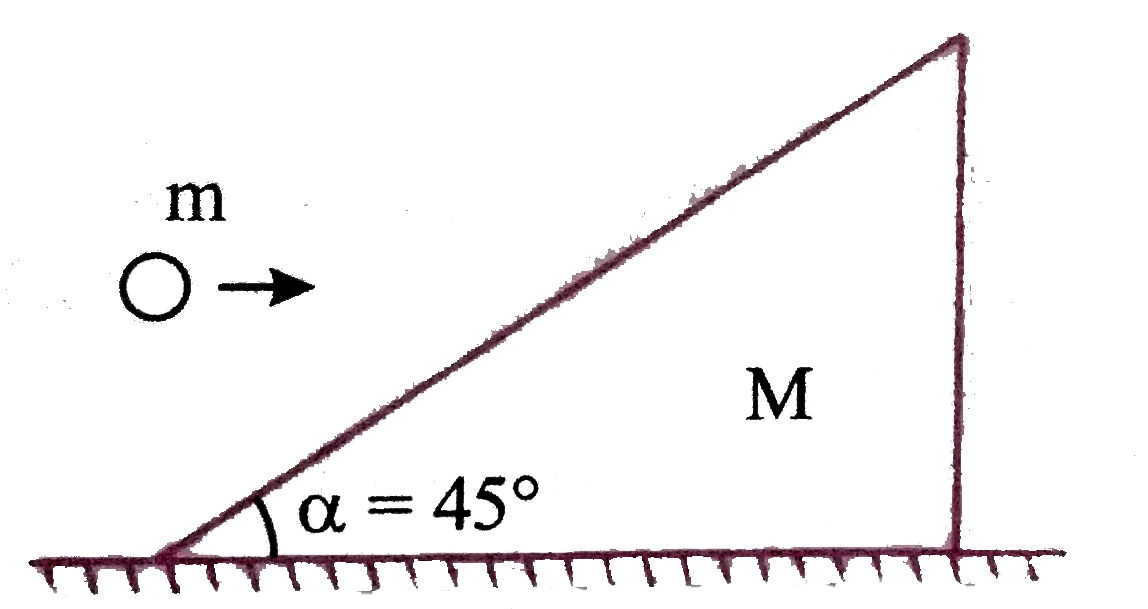
View SolutionA particle of mass 0.01 kg moving horizontally with velocity 20 m/s strikes a stationary wedge ABC of mass 0.05 kg with a velocity of 20 m/s near the apex of the wedge is free to move. Second collision of the particle with the wedge occurs at B. Find.
(a) the length AB of the wedge
(b) the normal reaction between the ground and the wedge during the first collision. [Given that angle θ=cot−1 (2)]

View SolutionA small block of mass m is kept on the inclined surface of a wedge of mass M. The inclined surface of the wedge makes an angle θ with the horizontal. The wedge is kept on a frictionless rigid horizontal floor. You can neglect friction between the block and the wedge also. An external agent applies a horizontal force F on the wedge.

The value of the force F so that the wedge remains at rest is F1. Which of the options is incorrect?
View Solution
