Two blocks of masses m1 and m2 are connected by a massless pulley A, slides along th esmooth sides of a rectangular wedge of mass m, which rests on a smooth horizontal plane. Find the distance covered by the wedge on the horizontal plane till the mass m1 is lowered by the vertical distance h.

The correct Answer is:(m2+m1cotα)hm+m1+m2
Δxcm=0=mx0+m1(x0−hcotα)+m2(x0−h)m+m1+m2
⇒x0=(m2+m1cotα)(m+m1+m2)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
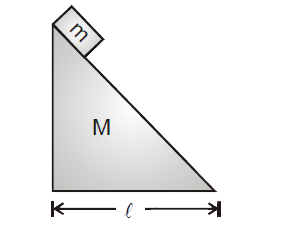
View Solution
Knowledge Check
A mass m is at rest on an inclined plane of mass M which is further resting on a smooth horizontal plane. Now if the mass starts moving, the position of centre of mass of the system will :
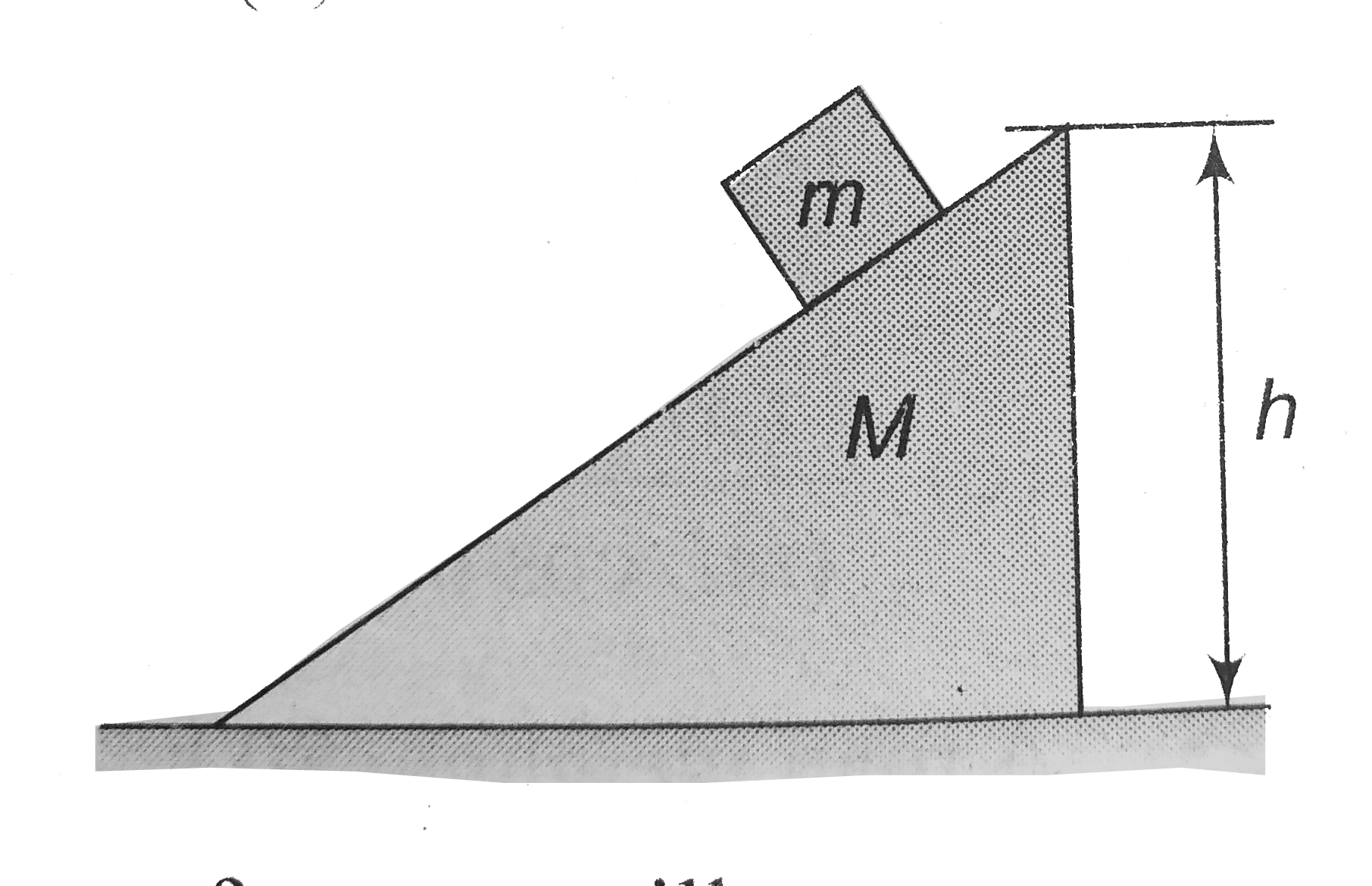 .Aremain unchangedBchange along the horizontalCmove up in the vertical directionDchange along the vertical while remains same along the horizontal
.Aremain unchangedBchange along the horizontalCmove up in the vertical directionDchange along the vertical while remains same along the horizontalA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest
 A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the above
A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the aboveTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of springAzeroBF(m1+m2)m1m2CFm1DFm1+m2
Two blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth horizontal plane.
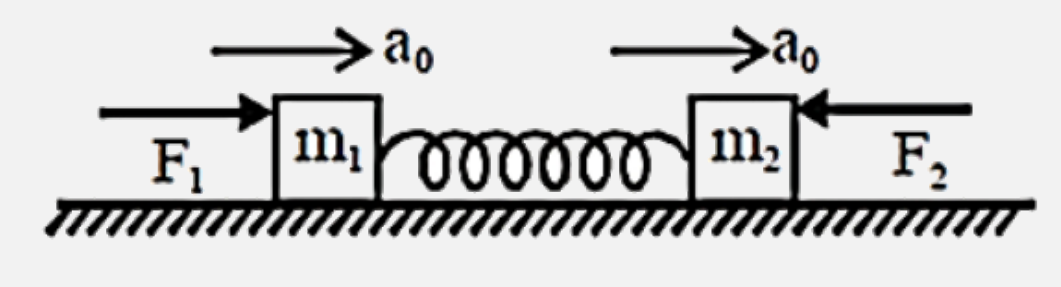
View SolutionTwo blocks of masses m1 = 3 kg and m2=1√3 kg are connected by a light inextensible string which passes over a smooth peg . The blocks rest on the inclined smooth planes of a wedge and the peg is fixed to the top of the wedge . The planes of the wedge supporting m1 and m2 are inclined at 30∘ and 60∘ respectively , with the horizontal. Calculate the acceleration of masses and the tension in the string .
View SolutionTwo smooth blocks of masses m and m' connected by a light inextensible strings are moving on a smooth wedge of mass M. If a force F acts on the wedge the blocks do not slide relative to the wedge. Find the (a) acceleration of the wedge and (b) value of F.

View SolutionA smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?
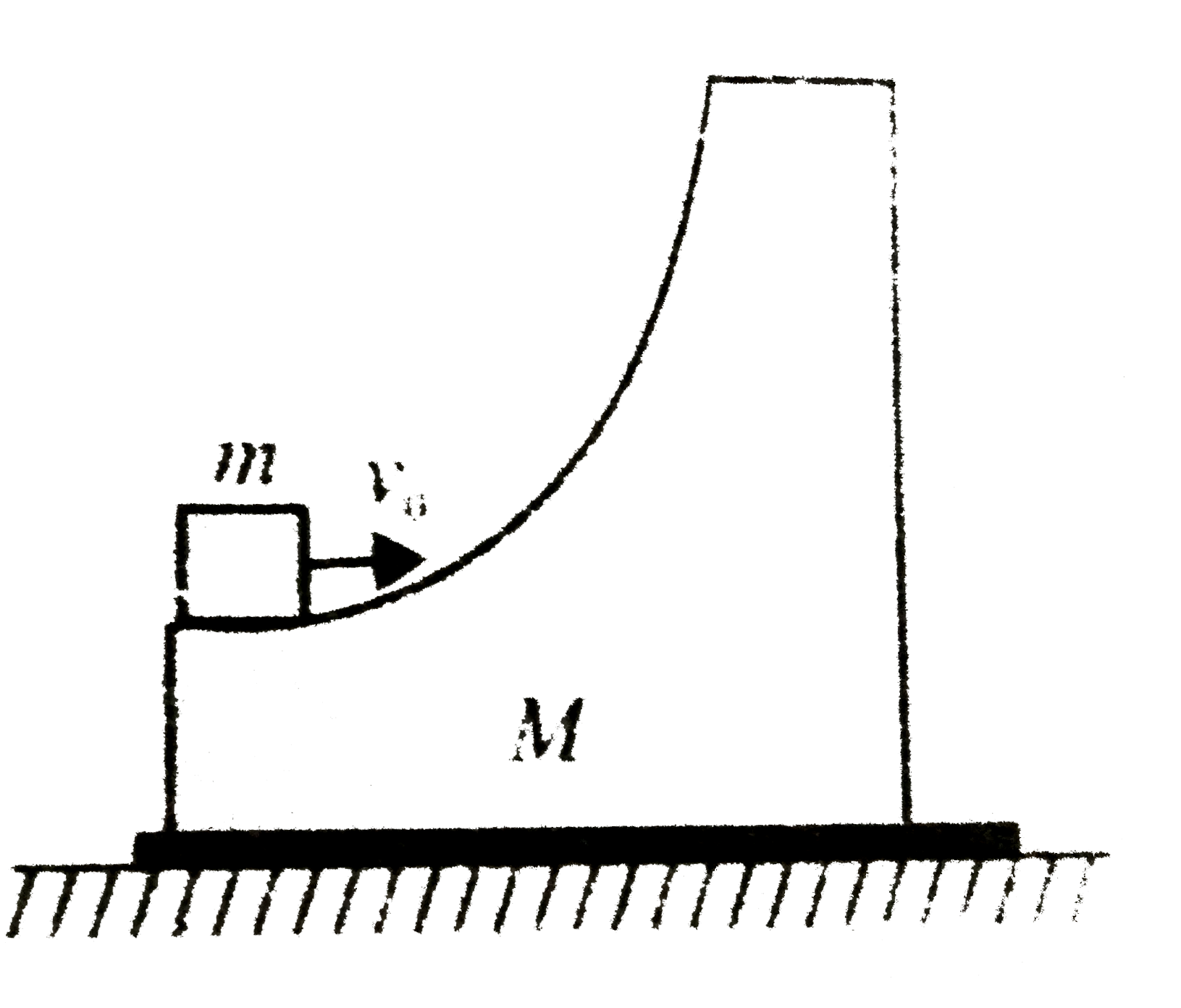
View Solution
