The Atwood machine in figure has a third mass attached to it by a limp string. After being released, the 2m mass falls a distance x before the limp string becomes laut. Thereafter both the mass on the left rise at the same speed. What is the final speed ? Assume that pulley is ideal.
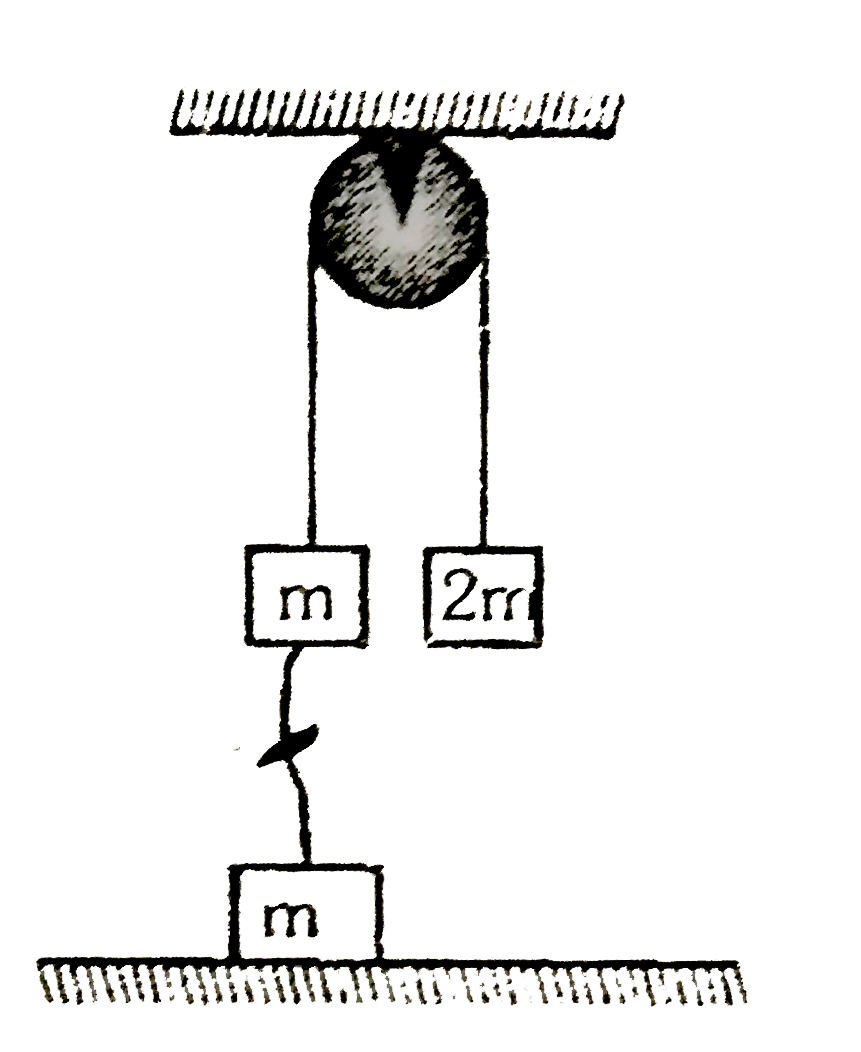
The correct Answer is:√3gx8
2mg−T=2ma,T−mg=ma,a=g3
Velocity of m & 2m after falling through a distance x=√2ax=√2gx3
Impulse equation
TΔt=2m(v−√2gx3)
TΔt−T'Δt=m(v−√2gx3)
T'Δt=m(v−0),v=√3gx8
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut.
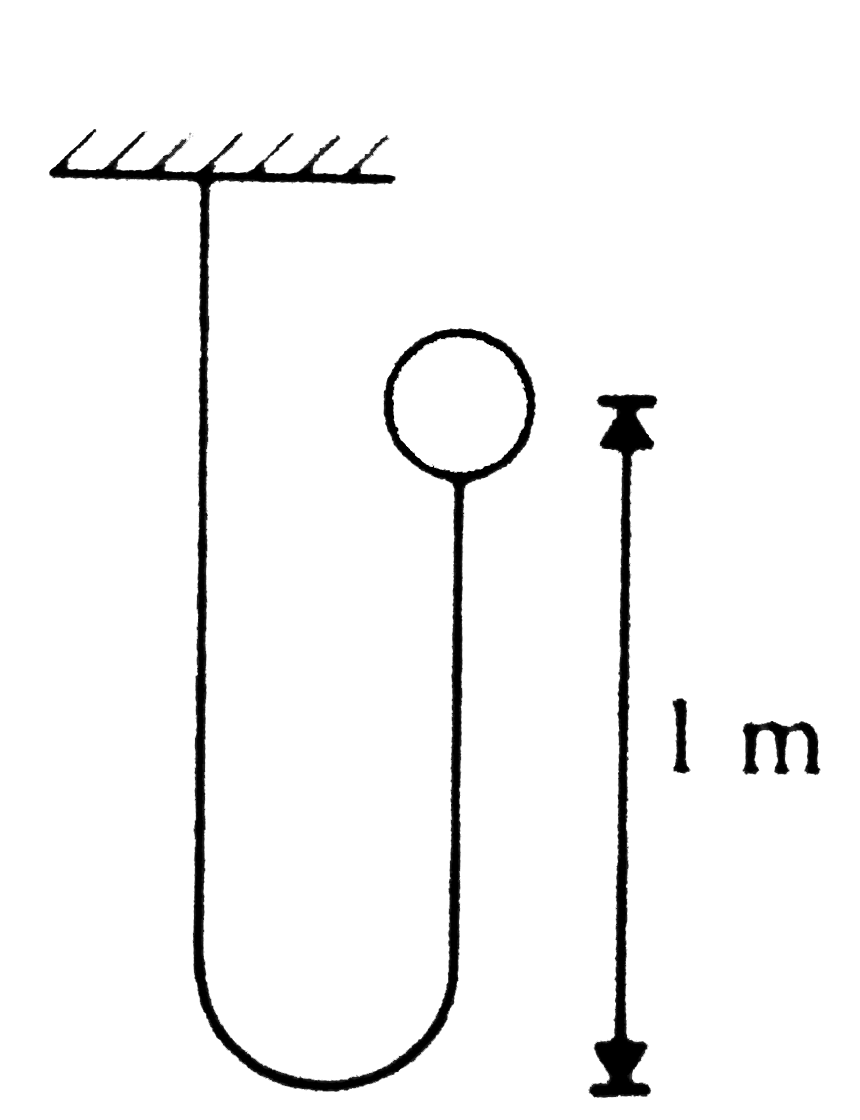
View SolutionA ball of mass 1.00 kg is attached to a loose string fixed to a ceiling. The ball is released from rest and falls 2.00 m, where the string suddenly stops it. Find the impulse on it from the string.
View Solution
Knowledge Check
Both the blocks shown in figure have same mass 'm'. All the pulley and strings are massiess.
 AAcceleration of block A is 2g5BAcceleration of block A is g5CAcceleration of block B is g5DTension in the attached with A is 3mg5
AAcceleration of block A is 2g5BAcceleration of block A is g5CAcceleration of block B is g5DTension in the attached with A is 3mg5A bead can slide on asmooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle θ with the wire, the bead will have slipped a dsitance.
 AL(1−cosθ)B(L2)(1−cosθ)C(L3)(1−cosθ)D(L6)(1−cosθ)
AL(1−cosθ)B(L2)(1−cosθ)C(L3)(1−cosθ)D(L6)(1−cosθ)A simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is
 A(a) cos−1[Lcosα+lL+l]B(b) cos−1[Lcosα+lL−l]C(c) cos−1[Lcosα−1L−l]D(d) cos−1[Lcosα−1L+l]
A(a) cos−1[Lcosα+lL+l]B(b) cos−1[Lcosα+lL−l]C(c) cos−1[Lcosα−1L−l]D(d) cos−1[Lcosα−1L+l]
Two particle A and B, of mass 3mand2m respectively, are attached to the ends of a light inextensible string which passes over a smooth fixed pulley of negligible mass. After the system is released and A falls through a distance L, it hits a horizontal inelastic table so that its speed is immediately reduced to zero. Assume that B never hits the table or the pulley. Find
(a) the time for which A is resting on the table after the first collision and before it is jerked off,
(b) the difference between the total kinetic energy of the system immediately before A first hits the table and total kinetic energy immediately after A starts moving upwards for the first time. Explain the loss in kinetic energy.

View SolutionA particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from the position as shown in Fig. Calculate
a. the impulse developed in the string when it becomes taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut. (Take g=10m/s2)

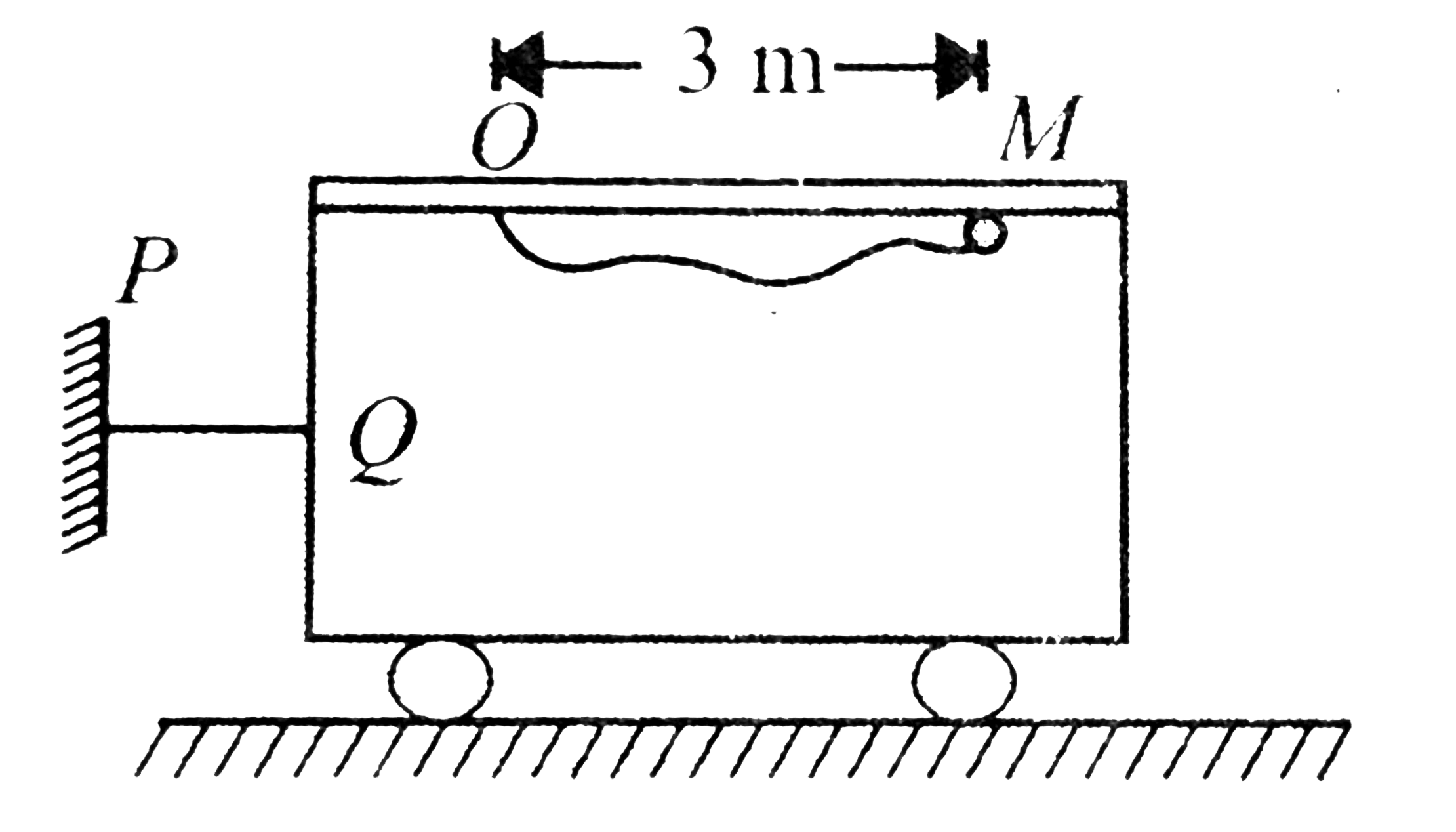
View SolutionA string with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of 2m from the wall, has a point mass M of 2kg attached to it at a distance of 1m from the wall. A mass m of 0.5kg is attached to the free end. The system is initially held at rest so that the stirng is horizontal between wall and pulley and vertical beyond the pulley as shown in figure.

What will be the speed with which point mass M will hit the wall when the system is released? (g=10ms−2)
View SolutionA stone of mass 250 gram , attached at the end of a string of length 1.25 m is whirled in a horizontal circle at a speed of 5 m/s . What is the tension in the string ?
View Solution
