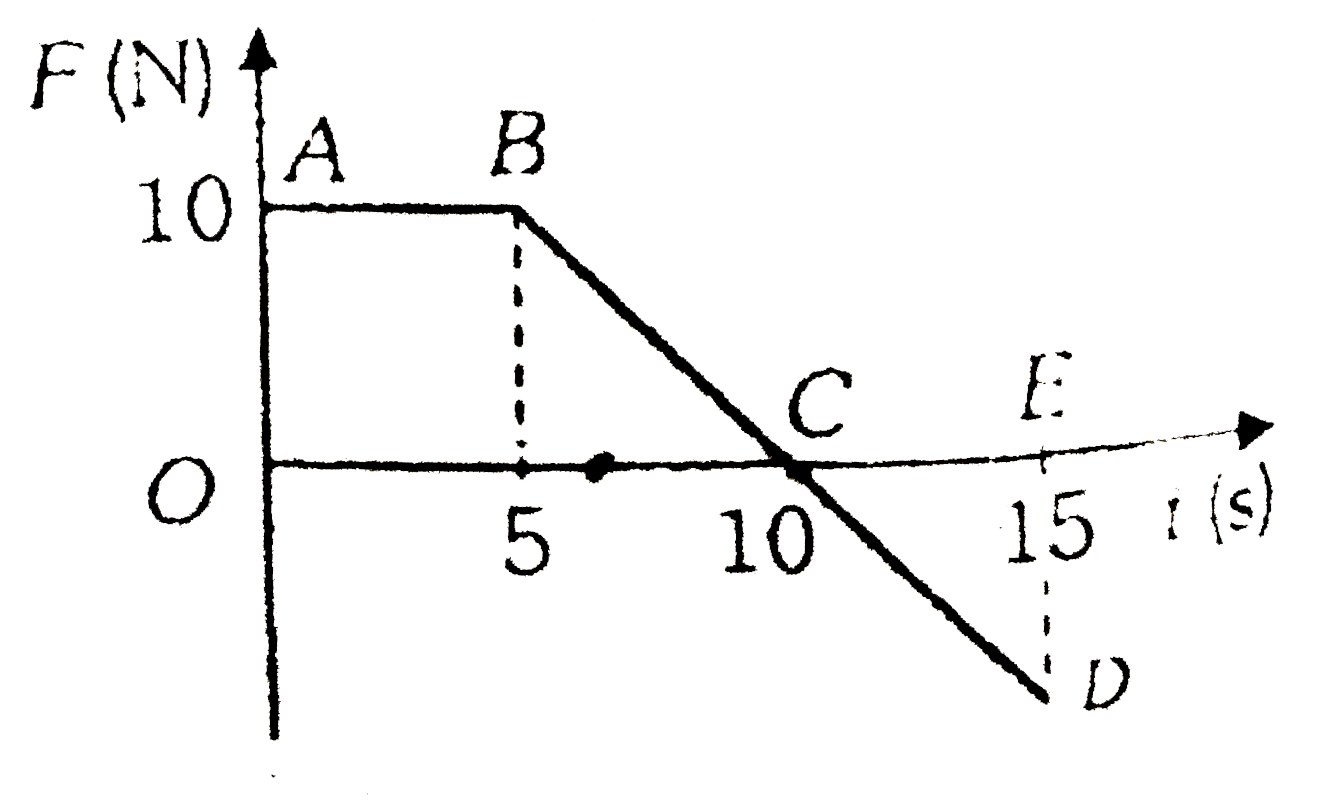
A one-dimensional force F varies with time according to the given graph. Calculate impulse of the force in following time intervals.
(a) From t=0s to t=10s.
From t=10s to t=15s.
(C) From t=0s to t=15s.
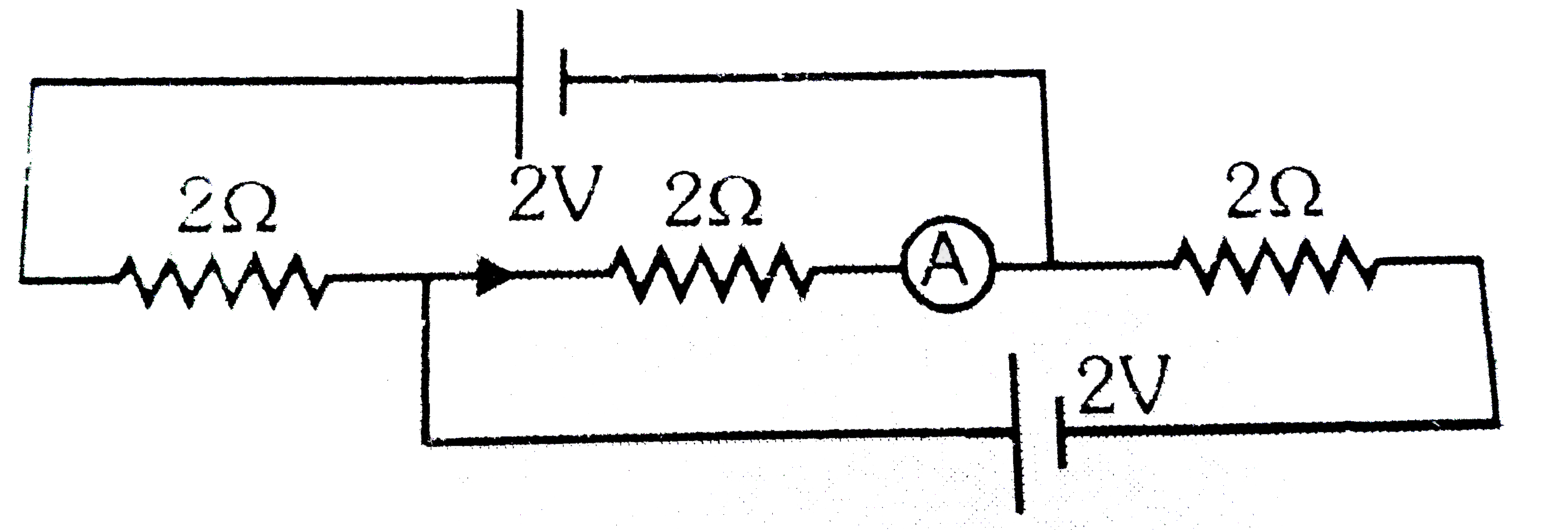
For one-dimensional force, impulse equals to area between force-time graph and the time axis. (a) I0→10= Area of trapazium OABC=75N−s
(b) I10→15=− Area of triangle CDE=−25N−s
(c ) I0→15= Area of trapazium OABC− Area of triangle CDE=50N−s
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-I
Explore 40 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-II
Explore 43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
Knowledge Check
Velocity of a particle of mass 2kg varies with time t according to the equation →v=(2tˆi+4ˆj)m/s. Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
A2ˆim/sB4ˆim/sC8ˆim/sD6ˆim/sA point moves in the straight line during the time t=0 to t=3 according to the law s=15t−2t2. The average velocity is
A3 unitsB9 unitsC15 unitsD27 units
The magnetic field through a single loop of wire, 12cm in radius and of 8.5Ω resistance, changes with time as shown in figure. Calculate the emf in the loop as a function of time. Consider the time intervals
(a) t=0 to t=2.0s (b) t=2.0s to t=4.0s (c) t=4.0s to t=6.0s.
The magnetic field is perpendicular to the plane of the loop.

View SolutionDisplacement of a particle of mass 2 kg varies with time as s=(2t2−2t+10)m. Find total work done on the particle in a time interval from t=0 to t=2s.
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
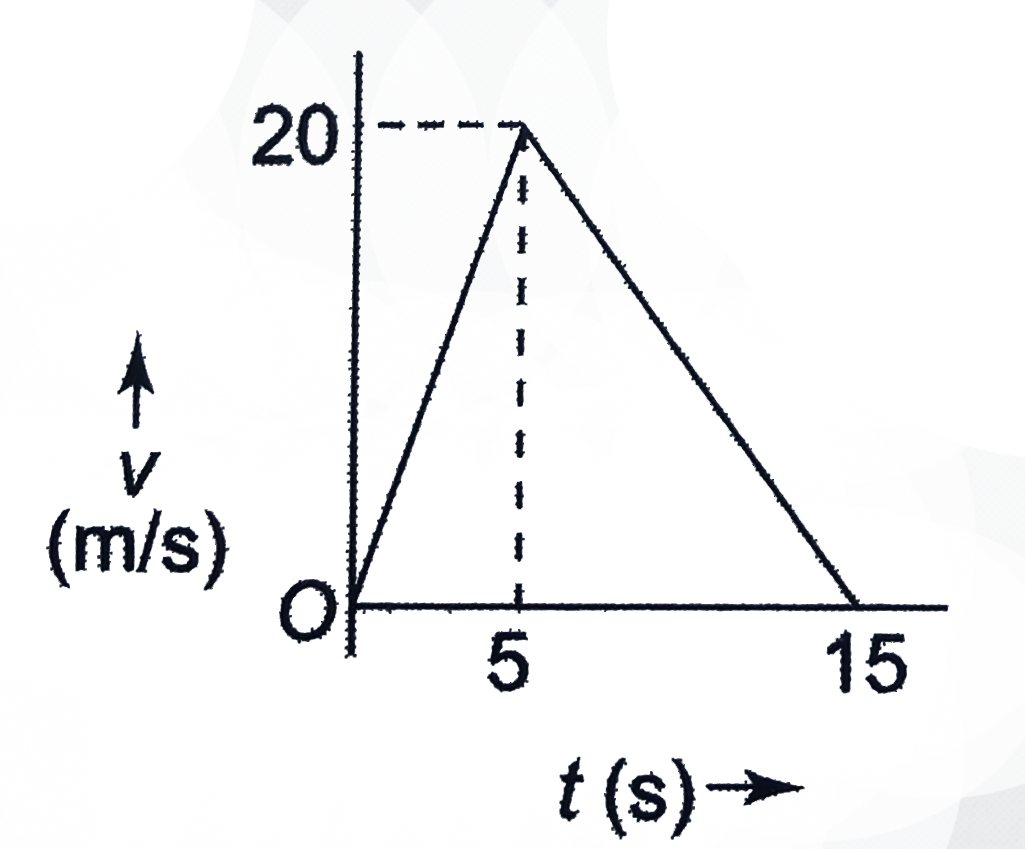
View SolutionFrom the following v-t graph, find the displacement for time interval t=3 to t=12s.
View SolutionA particle is at x=5m at t=0,x=−7m at t=6s and x=+2m at t=10s, find the average velocity of the particle during the interval (a) t=0 to t=6s, (b) t=6s to t=10s, (c) t=0 to t=10s
View SolutionA particle moves rectilinearly possessing a parabolic s-t graph. Find the average velocity of the particle over a time interval from t=12s→t=1.5s.
View Solution

