From the following v-t graph, find the displacement for time interval t=3 to t=12s.
To determine the displacement for t=3 to t=12s, we require velocities at these instances.
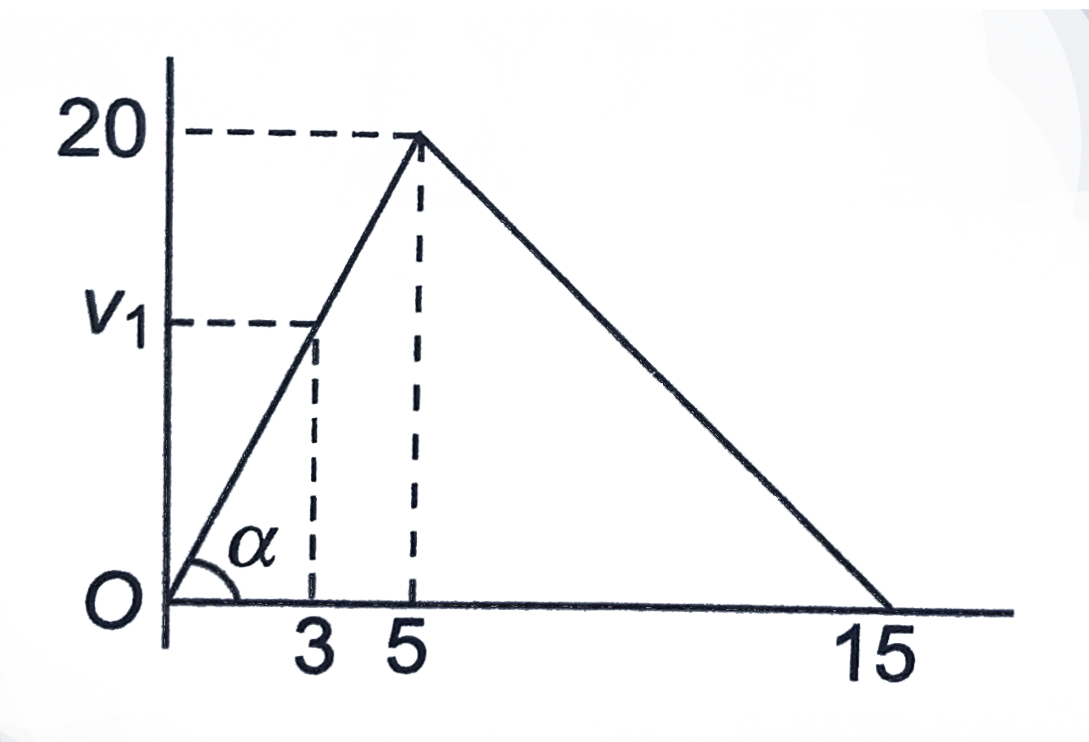
tanα=v13=205⇒v1=12m/s
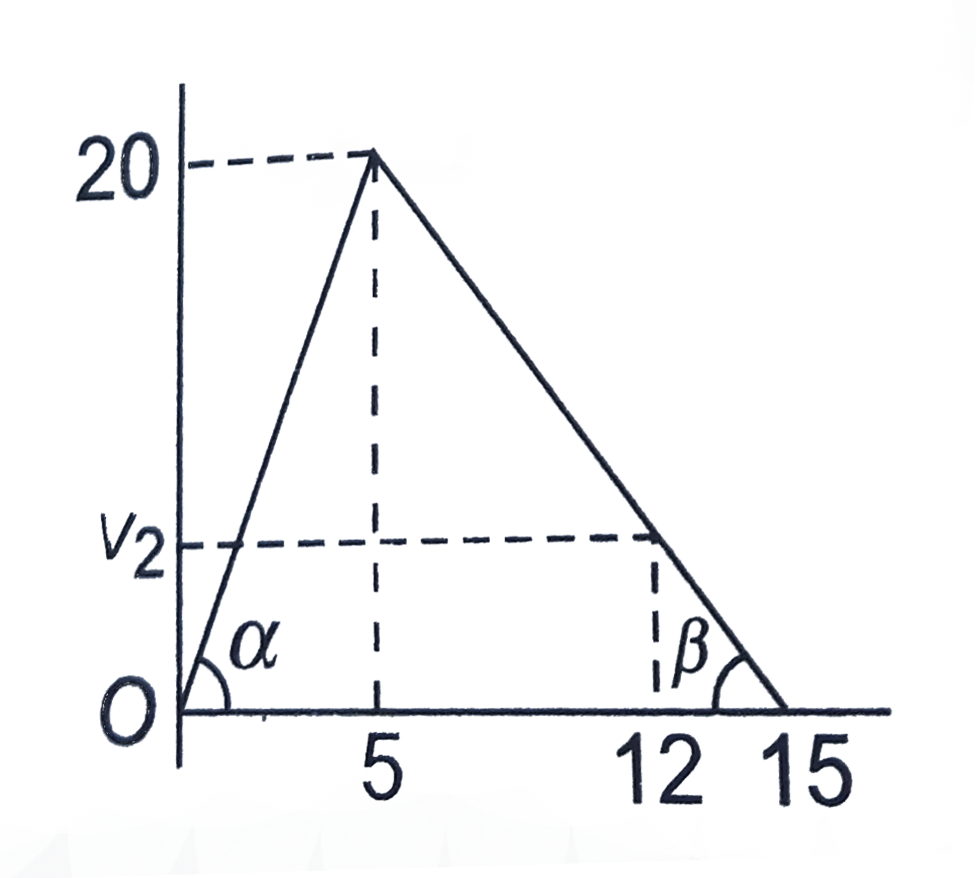
tanβ=v2(15−12)=20(15−5)⇒v2=6m/s
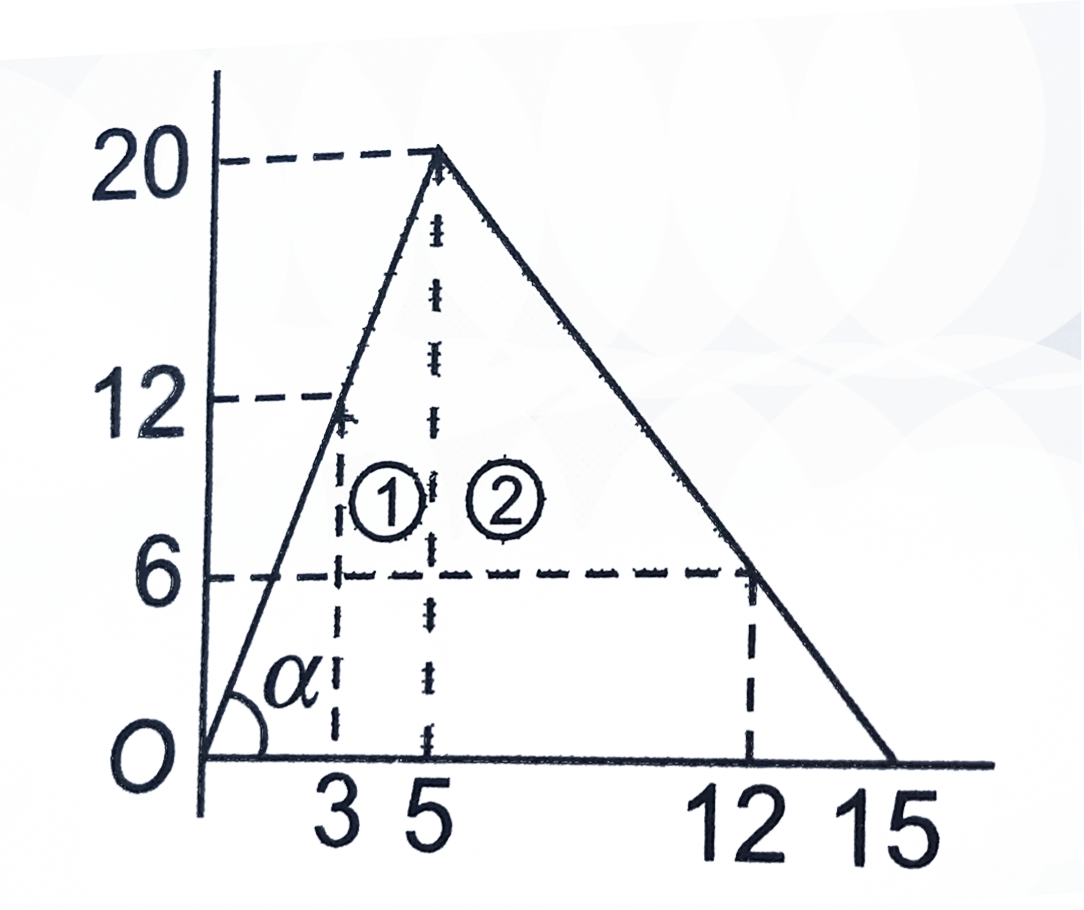
Area of trapezium (1)=12(12+20)×2=32
Area of trapezium (2) =12(6+20)×7=91
For t=3 to 12s, Displacement =32+91=123m
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which of the following graphs represents the displacement (s) -time (t) graph for uniform motion ?
A B
B C
C D
D
A particle is moving with a velocity of v=(3+6t+9t2)ms. Find out
(a) the acceleration of the particle at t=3s.
(b) the displacement of the particle in the interval t=5s to t=8s.A60B20C10D15
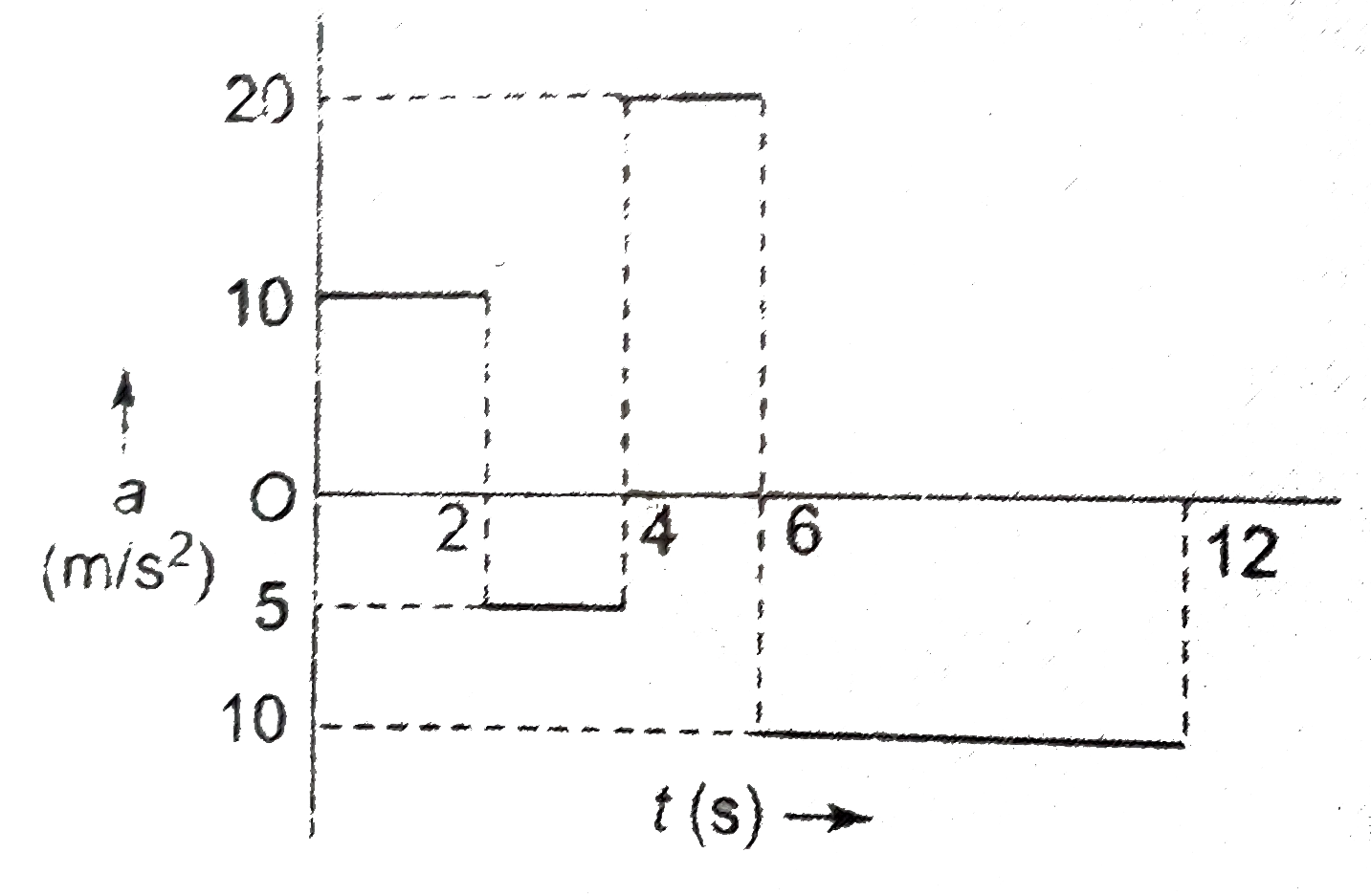
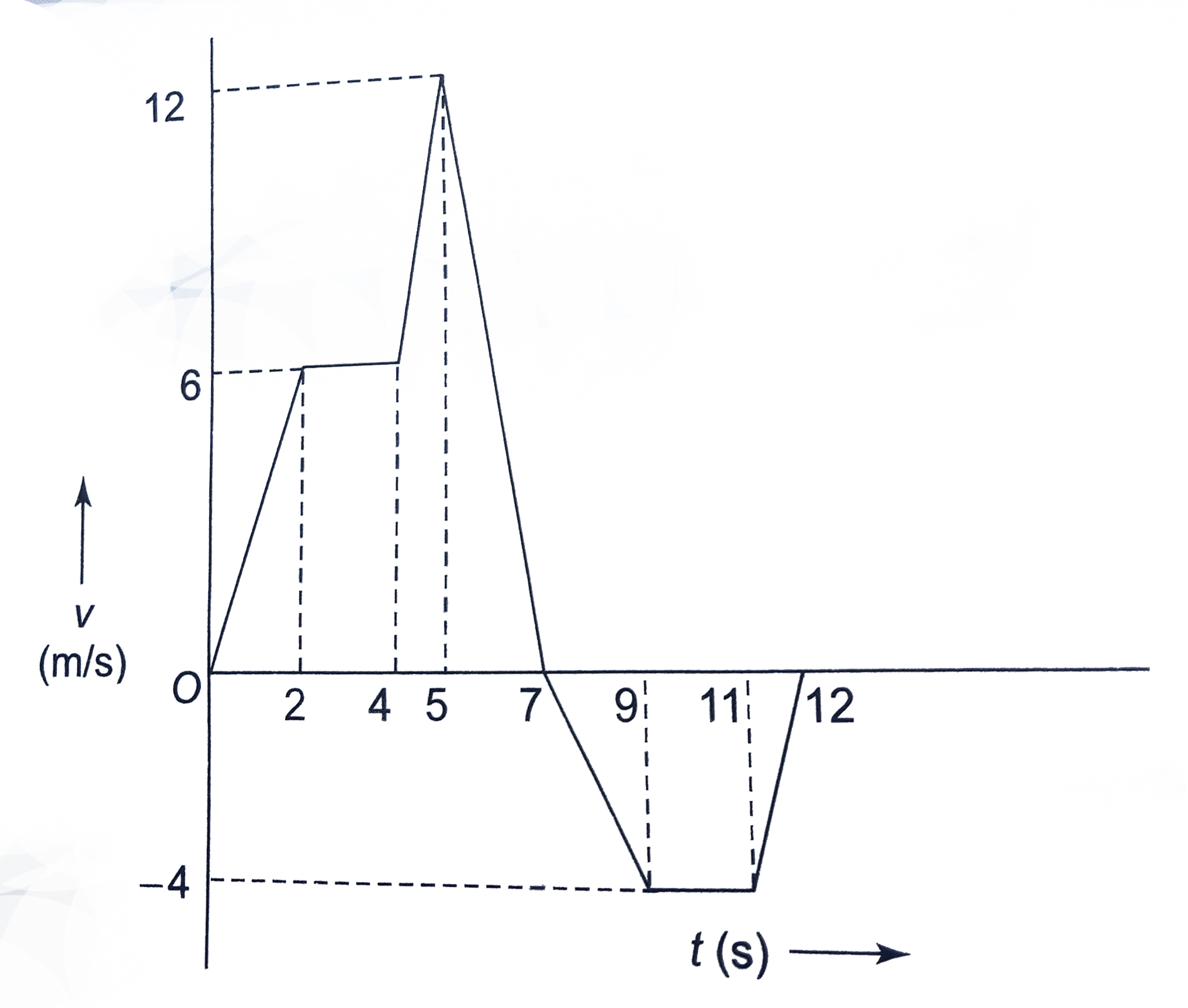
Study the following velocity-time graph. Determine the displacement and distance in the time interval t=0 to t=12s. Sketch the acceleration-time graph.
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=0 s to t=1 s.
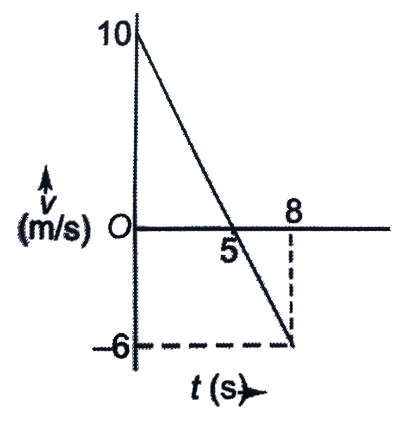
View SolutionA particle is moving in a straight line. Its v-t graph in different cases are as shown below. Find the diplacement and distance in time interval t=0 to t=10 s for the following cases:

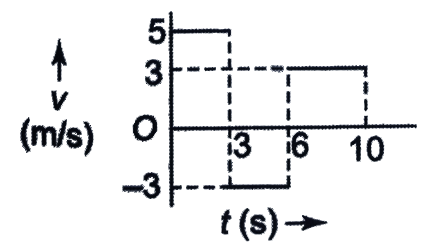
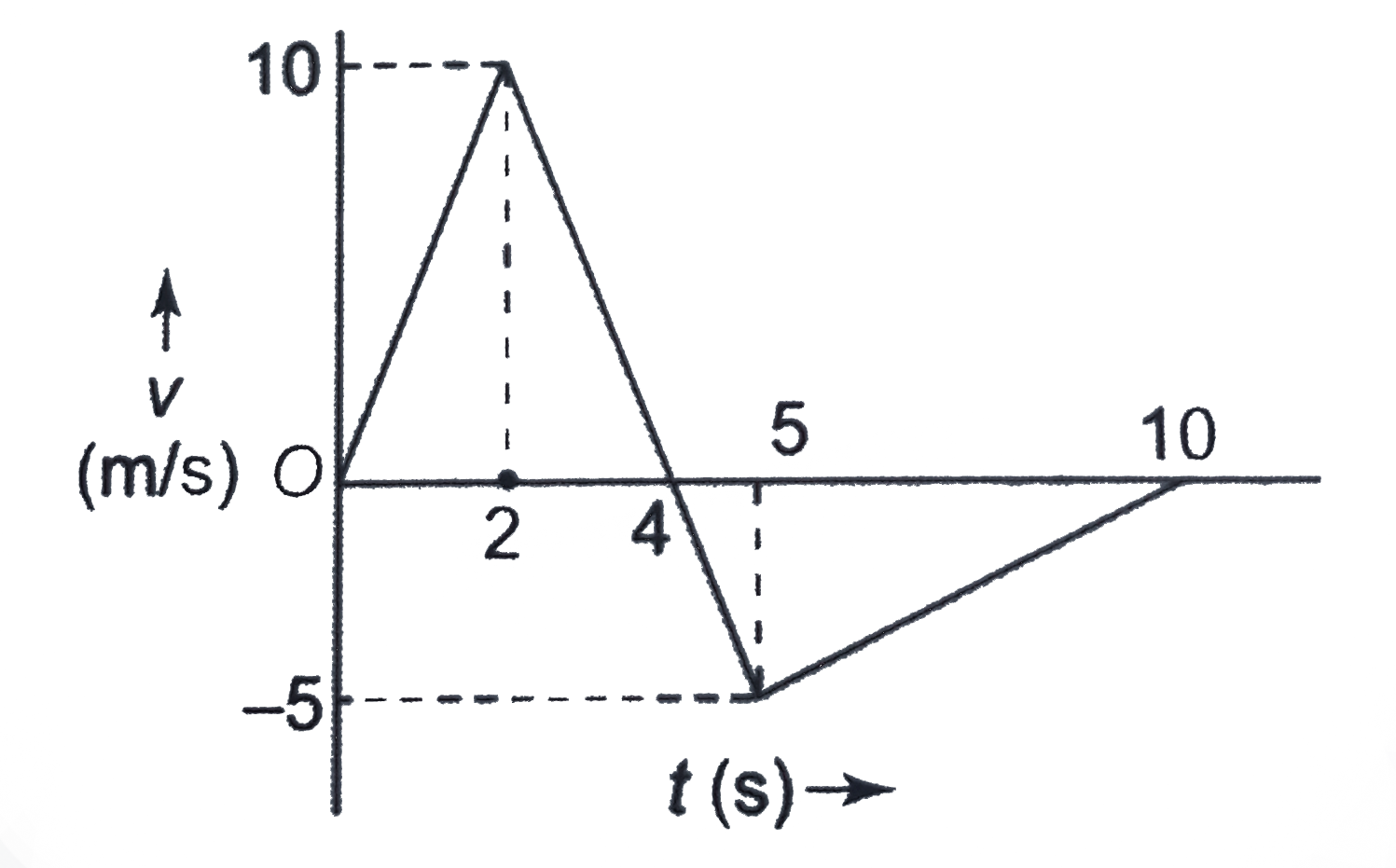
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=1sto t=3s.
View SolutionA particle is moving in a straight line along X-axis and its x-coordinate varies with time as:
x=t2−4t+6
Find the distance and displacement of particle in time interval t=0to t=3s.
View SolutionThe position of a particle varies with time according to the relation x=3t2+5t3+7t, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.
View Solution