In S.H.M., potential energy (U) V/s, time (t) . Graph is
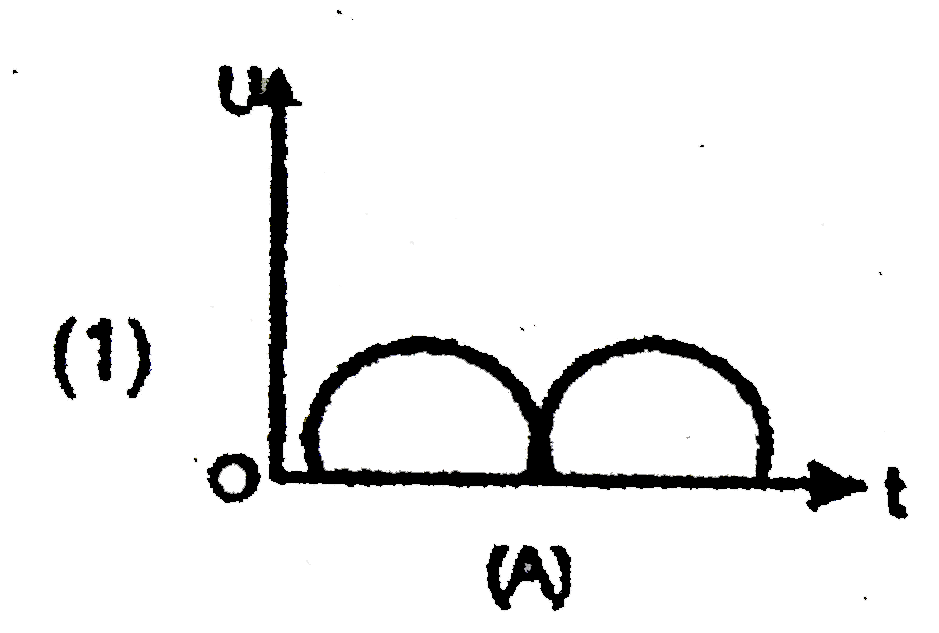
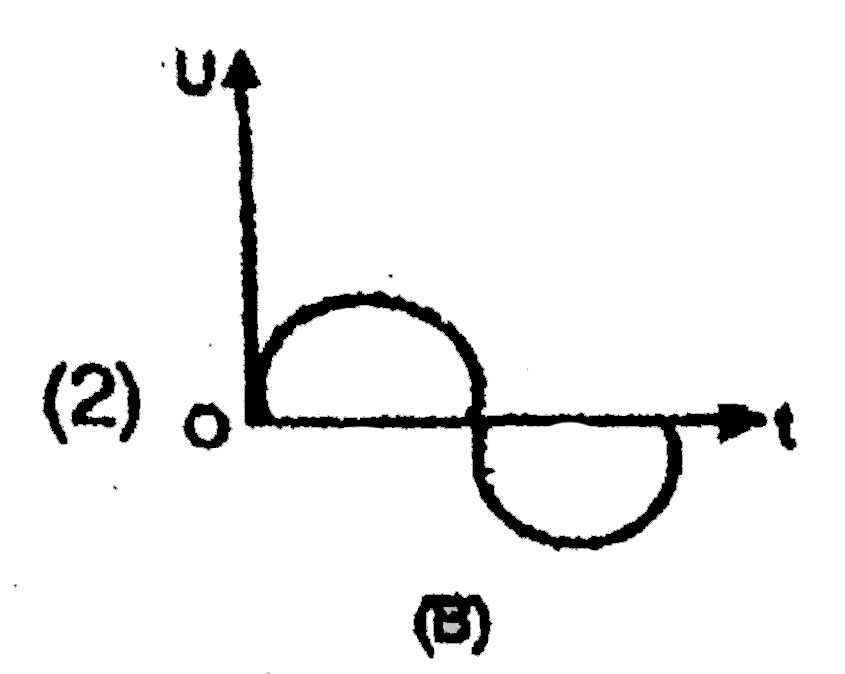


The correct Answer is:A
To determine the potential energy versus time graph for a particle undergoing simple harmonic motion (S.H.M.), we can follow these steps:
1. Understand the Equation of S.H.M.:
The displacement x of a particle in S.H.M. can be described by the equation:
x(t)=Asin(ωt+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
2. Potential Energy in S.H.M.:
The potential energy U of a particle in S.H.M. is given by:
U=12kx2
where k is the spring constant.
3. Substituting the Displacement:
Substitute the expression for x(t) into the potential energy formula:
U(t)=12k(Asin(ωt+ϕ))2
This simplifies to:
U(t)=12kA2sin2(ωt+ϕ)
4. Analyzing the Graph:
The term 12kA2 is a constant. The potential energy U(t) is proportional to sin2(ωt+ϕ). The graph of sin2(x) oscillates between 0 and 1, meaning U(t) will oscillate between 0 and 12kA2.
5. Graph Characteristics:
- The graph will always be above the time axis (since sin2 is always non-negative).
- If ϕ=0, the graph starts at U=0 when t=0.
- If ϕ is not zero, the graph will be shifted horizontally.
6. Final Graph:
The resulting graph of potential energy versus time will be a sinusoidal wave that oscillates between 0 and 12kA2, resembling a sine squared function.
The displacement x of a particle in S.H.M. can be described by the equation:
x(t)=Asin(ωt+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
The potential energy U of a particle in S.H.M. is given by:
U=12kx2
where k is the spring constant.
Substitute the expression for x(t) into the potential energy formula:
U(t)=12k(Asin(ωt+ϕ))2
This simplifies to:
U(t)=12kA2sin2(ωt+ϕ)
The term 12kA2 is a constant. The potential energy U(t) is proportional to sin2(ωt+ϕ). The graph of sin2(x) oscillates between 0 and 1, meaning U(t) will oscillate between 0 and 12kA2.
- The graph will always be above the time axis (since sin2 is always non-negative).
- If ϕ=0, the graph starts at U=0 when t=0.
- If ϕ is not zero, the graph will be shifted horizontally.
The resulting graph of potential energy versus time will be a sinusoidal wave that oscillates between 0 and 12kA2, resembling a sine squared function.
Topper's Solved these Questions
Similar Questions
A time varying voltage V= 2t (Volt) is applied across and ideal inductor of inductance L =2H as shown in Fig. Then (assume current to be zero at t =0)

View SolutionWhich of the following graph is correct between kinetic energy E, potential energy (U) and height (h) from the ground of the partical
View Solution
Knowledge Check
When the displacement of a particle in S.H.M. is 0.2m, its Potential energy is equal to 2 J. The force constant of the S.H.M. is
A100N/mB50N/mC200N/mD25N/mFor a particle executing S.H.M., the kinetic energy K is given K=K0cos2ωt. The maximum value of potential energy is:
AK0BzeroCK0/2Dnot abtainableWhich of the following graph is correct between kinetic energy E, potential energy (U) and height (h) from the ground of the partical
A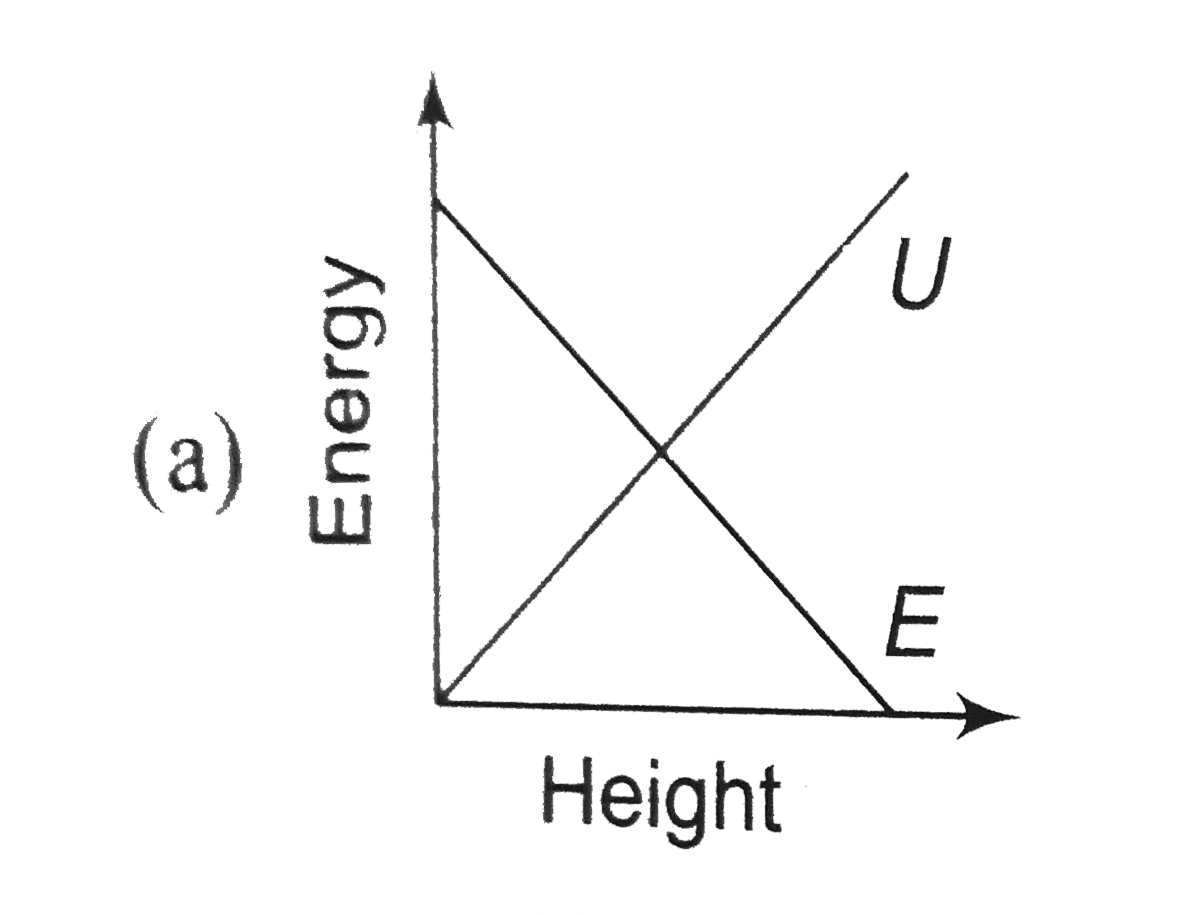 B
B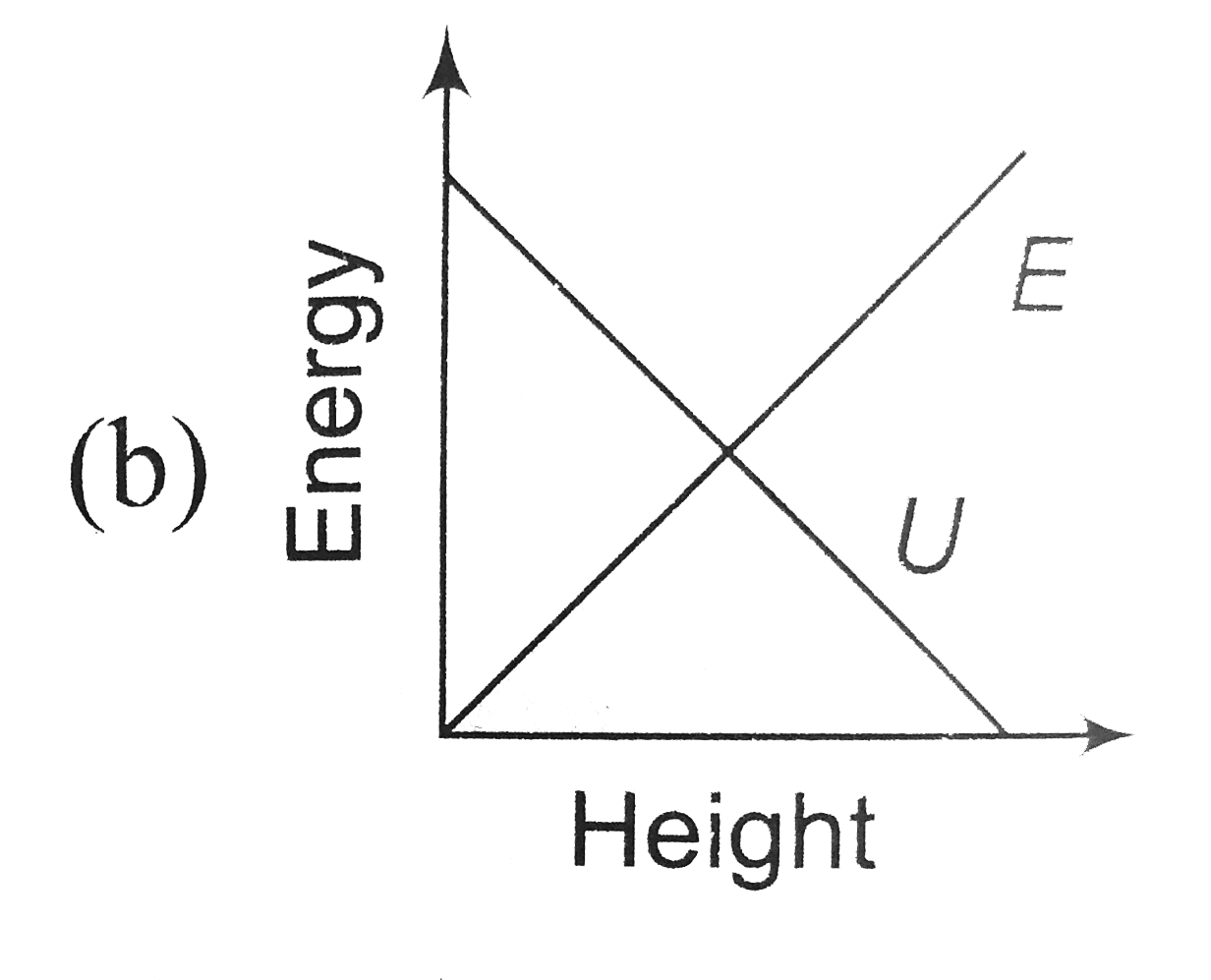 C
C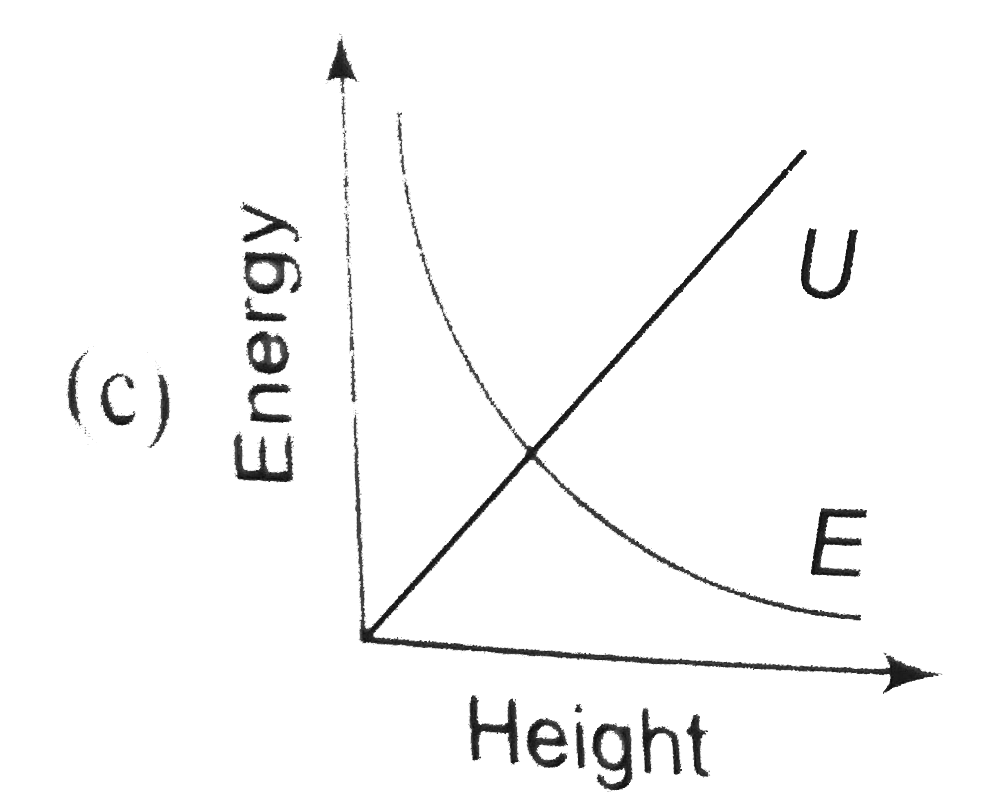 D
D
As a body performs SHM its potential energy U. varies with time as indicated in
View SolutionIn S.H.M., the graph between kinetic energy K and time 't' is
View SolutionA body performs S.H.M. Its kinetic energy K varies with time t as indicated by graph
View SolutionAt the surface of earth, potential energy of a particle is U and potential is V.Change in potential energy and potential at height h=R are suppose ΔU and ΔV.Then
View SolutionThe potential energy of a particle perfonning S.H.M. is
View Solution
