The amplitude of a particle performing SHM is 'a'. The displacement at which its velocity will be half the maximum velocity is
√32a
3√2a
a/2
a
The correct Answer is:A
v=ω√a2−x2
aω2=ω√a2−x2
x=√32a
Topper's Solved these Questions
Similar Questions
A particle is performing SHM. At what distance from mean position, the velocity of the particle becomes half of the maximum velocity ?
View SolutionA graph between velocity and displacement of a particle performing SHM is shown. Find the acceleration when the particle is at half of maximum displacement from mean position.
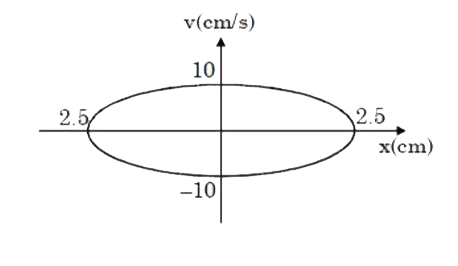
View Solution
Knowledge Check
The amplitude of particle performing S.H.M. is
AtensorBvectorCscalarDdepending upon magnitudeA particle is executing S.H.M. with amplitude 'A' and maximum velocity Vm. The displacement at which its velocity is half of the maximum velocity is
A86.6%AB13.4%AC70.7%AD36.72%AThe velocity of a particle performing S.H.M. at any position
Aleads in phase by (π/2) than the displacementBlags in phase by (π/2) than the displacementCleads in phase by (π/2) than the accelerationDa' and 'b'
The velocity of a particle performing S.H.M. at mean position is
View SolutionA simple harmonic oscillator has amplitude 2 A and maximum velocity 2 V. Then its displacement at which its velocity is V and the velocity at displacement A are
View SolutionThe velocity of a particle performing S.H.M. at extreme position is
View SolutionThe equation of displacement of a particle performing a S.H.M. is x=0.25 "sin" (200 t) metre. What is the maximum velocity of the particle ?
View SolutionThe velocity of a particle performing linear S.H.M. at mean position is v0. What will be its velocity at the mean position when its amplitude is doubled and time period reduced to l /3 ?
View Solution
