Question

A quadrilateral has vertices $(4,1),(1,7),(-6,0)$ AND $(-1,-9)$. Show that mid-points of the sides of this quadrilateral form a parallelogram.

Explanation

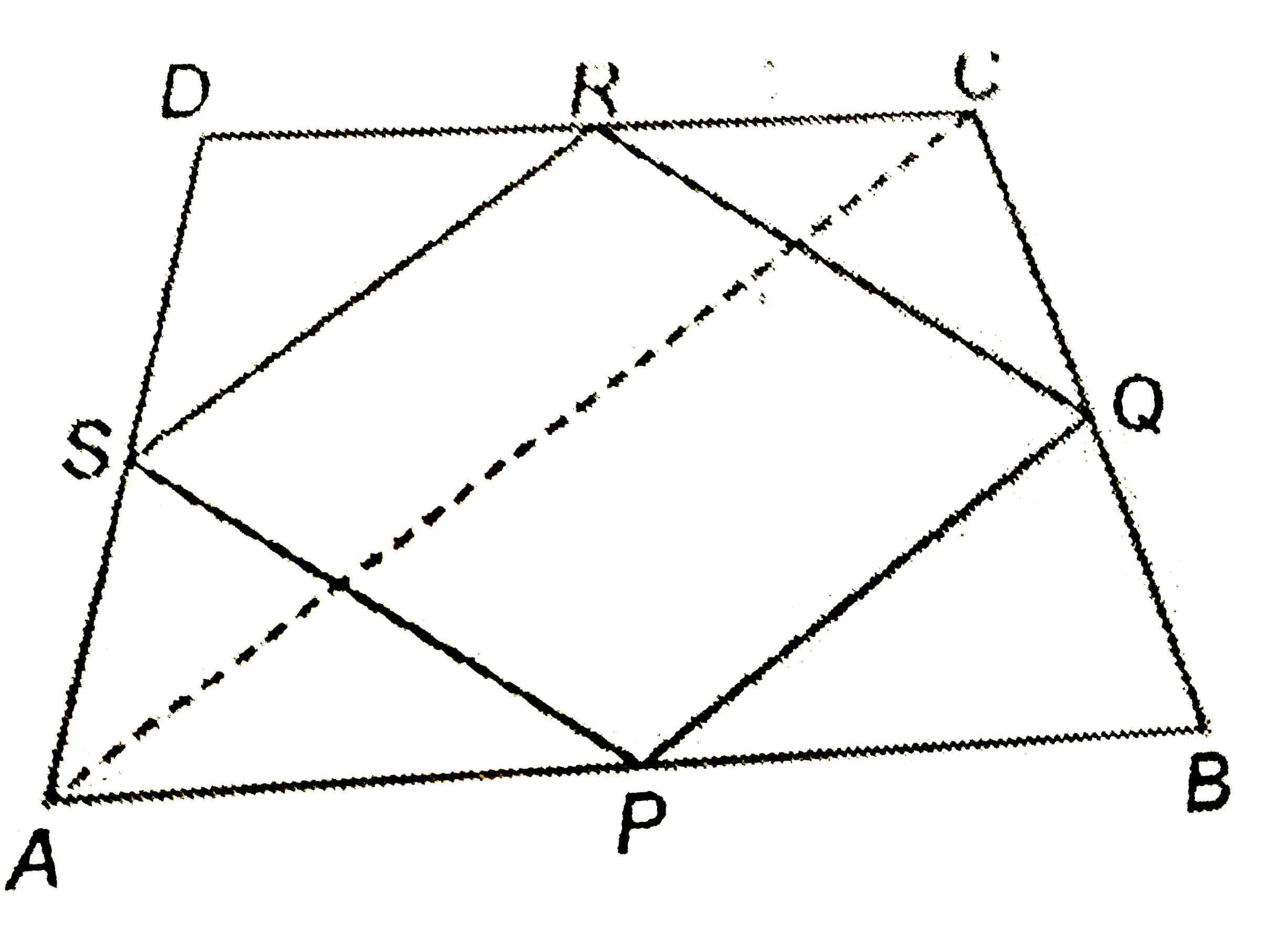
Let` A(4,1`), `B(1,7)`, `C(-6,0)` and `D(-1,-9)` be the vertices of the given quadrilateral.

Let P, Q, R and S be the mid-points of A B, B C, C D and D A, respectively.

So, the coordinates of P, Q, R and S are

`P(frac[5]2, 4), Q(frac[-5]2, frac[7]2), R(frac[-7]2, frac[-9]2)` and` S(frac[3]2,-4).`

In order to prove that PQRS is a parallelogram, it is sufficient to show that PQ is parallel to R S andPQ is equal to R S.

Now, we have,

Slope of PQ


`=frac({frac[7]2-4}[frac[-5]2-frac[5]2])=[frac[1]10]`

Slope of R S=`frac-4+frac[9]2frac[3]2+frac[7]2=frac[1]10`

Clearly, Slope of PQ = Slope of RS

Therefore, PQ

|| RS P Q=`sqrt(-frac[5]2-frac[5]2)^2+(frac[7]2-4)^2=fracsqrt[101]2`


R S=`sqrt(frac[3]2+frac[7]2)^2+(-4+frac[9]2)^2=fracsqrt[101]2`


Therefore, PQ=RS

Thus, P Q | R S and P Q=R S

Hence, the mid-points of the sides of the given quadrilateral form a parallelogram.