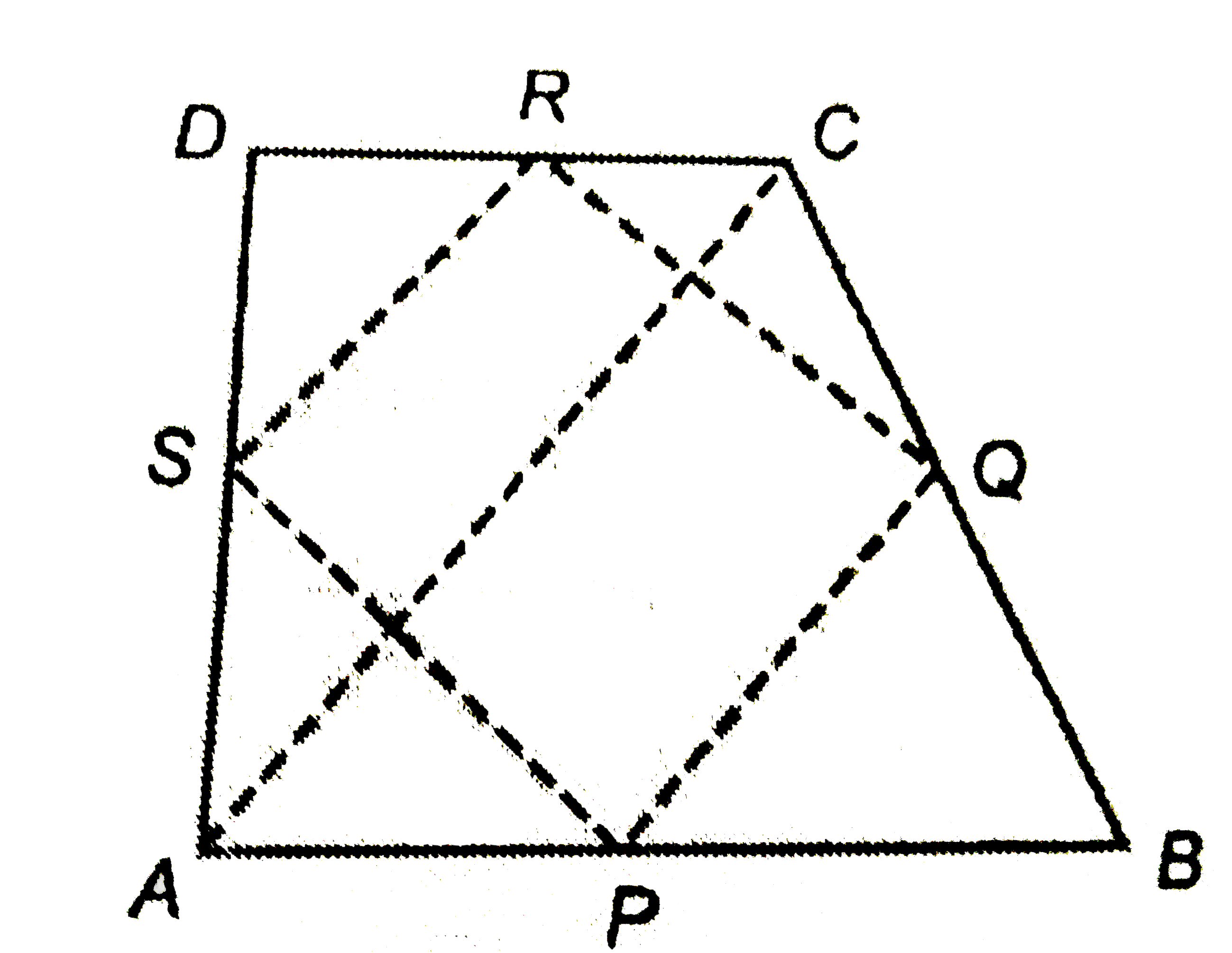
Show that the lines joining the mid-points of opposite sides of a quadrilateral bisect each other.
Let P, Q R and S are the mid-points of the sides AB, BC, CD and DA respectively of □ABCD. Join AC.,
Since, P and Q are the mid-points of BA and BC respectively.
∴PQ||ACandPQ=12AC (mid-point theorem) ...(1)
In ΔDAC,
Since, R and S are th mid-points of DC and DA respectively.
∴RS||ACandRS=12AC (mid-point theorem) ...(2)
From equations (1) and (2)
PQ||RSandPQ=RS
⇒□PQRS is a parallelogram (thereforeone pair of opposite side is equal and parallel)
We know that the diagonals of a parallelogram bisect each other.
∴ PR and QS bisect each other.
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Problems From NCERT/exemplar
Explore 11 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHANChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHANChapter:STATISTICSExercise:Revision Exercise
Explore 10 Videos
Similar Questions
Prove that line joining the midpoints of opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionProve that the lines joining the middle points of opposite sides of a quadrilateral and the line joining the middle points of its diagonals meet in a point and bisect one another.
View SolutionProve that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
View SolutionABCD is a quadrilateral and O is point in its plabe such that →OA+→OB+→OC+→OD=0 Show that O is the point of intersection of the lines joining the mid points of the opposite sides of quadrilateral ABCD.
View SolutionUsing vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View Solutioni. Show that the lines joining the vertices of a tetrahedron to the centroids of opposite faces are concurrent.
ii. Show that the joins of the midpoints of the opposite edges of a tetrahedron intersect and bisect each other.
View SolutionProve that the line joining the mid-points of the two sides of a triangle is parallel to the third side.
View Solution

