The Schrodinger equation for a free electron of mass m and energy W written in terms of the wave function Ψ is d1Ψdx2+8π2mEh2Ψ=0. The dimensions of the coefficient of Ψ in the second term must be
[M1L1]
[L2]
[L−2]
[M1L−1T1]
The correct Answer is:C
h=EλC
mEC2(Eλ)2=mEC2E2λ2=M1(L1T−1)2M1L2T−2L2=L2T−2L2T−2L2=L−2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.41
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.42
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.39
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Knowledge Check
For the wave function
Ψ=√281√πa3/20[6−ra0]ra0×e−r/3a0sinθ.cosϕ
Identify the orbital .A3pxB3pyC3pzD6pxor6pyor6pzIf ∫xlog(1+x2)dx=ϕ(x)log(1+x2)+x(Ψ)+C, then
Aϕ(x)=1+x22BΨ(x)=1+x22CΨ(x)=−1+x22Dϕ(x)=−1+x22The Schrodinger wave equation for H-atom is
∇2Ψ=8π2mh2(E−V)Ψ=0
Where ∇2=∂2∂x2+∂2∂y2+∂2∂z2
E = Total energy and V=potential energy wave function Ψ(rθϕ)R(r)Θ(θ)Φ(ϕ)
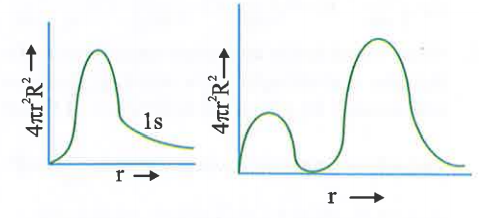
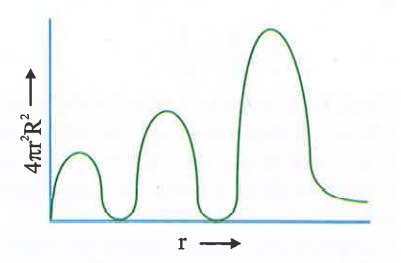
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. Θ and Φ are angular wave function. R2 is known as radial probability density and 4πr2R2dr is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
Ψ1s=√1πaa0e−zr/a0
Ψ2s=(Z2a0)½(1−Zra0)e−Zra0
The plot of radial probability function 4πr2R2 aganist r will be:
Answer the following questions:
The following graph is plotted for ns-orbitals
The value of 'n' will be:A1B2C3D4
What physical meaning is attributed meaning is attributed to the square of the absolute value of wave function ∣∣Ψ2∣∣ ?
View SolutionFind the distance at which probability of finding electron is maximum for 1s orbital in a He atom. The wave function orbital given as.
ψ1s=4a3/20e2ra0
View SolutionWhat physical meaning is attributed meaning is attributed to the square of the absolute value of wave function ∣∣Ψ2∣∣ ?
View SolutionFind the energy of an electron fo a hydrogen atom in a stationary state for which the wave function takes the from Ψ(r)=A(1+ar)e−αr, where A,aandα are constant.
View SolutionOne of the major requirement in atomic structure is determination of location of electron inside an atom. The wave mechanical model establishes this in accordance with Heisenberg's uncertainity principle through the concept of orbitals. The orbitals are defined as that '3D' space in which probability of finding electron is maximum and are represented by wave functions Ψn,l,m where n,l and m are quantum number. The variation of Ψ is analysed in terms of polar coordinates and hence Ψ=f(r,0,ϕ) where 'r' represents radius vector and 0 and ϕ represents angle (∠) Which the radius vector with x-axis respectively. The expressions of Ψr,0,ϕ are often given in terms of σ instead of r where σ=2Zrnα0 and Z = atomic number and n= shell number.
Which of the following statement is incorrect with respect to Ψ(r)us. r graph for H-atom?
View Solution