A mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
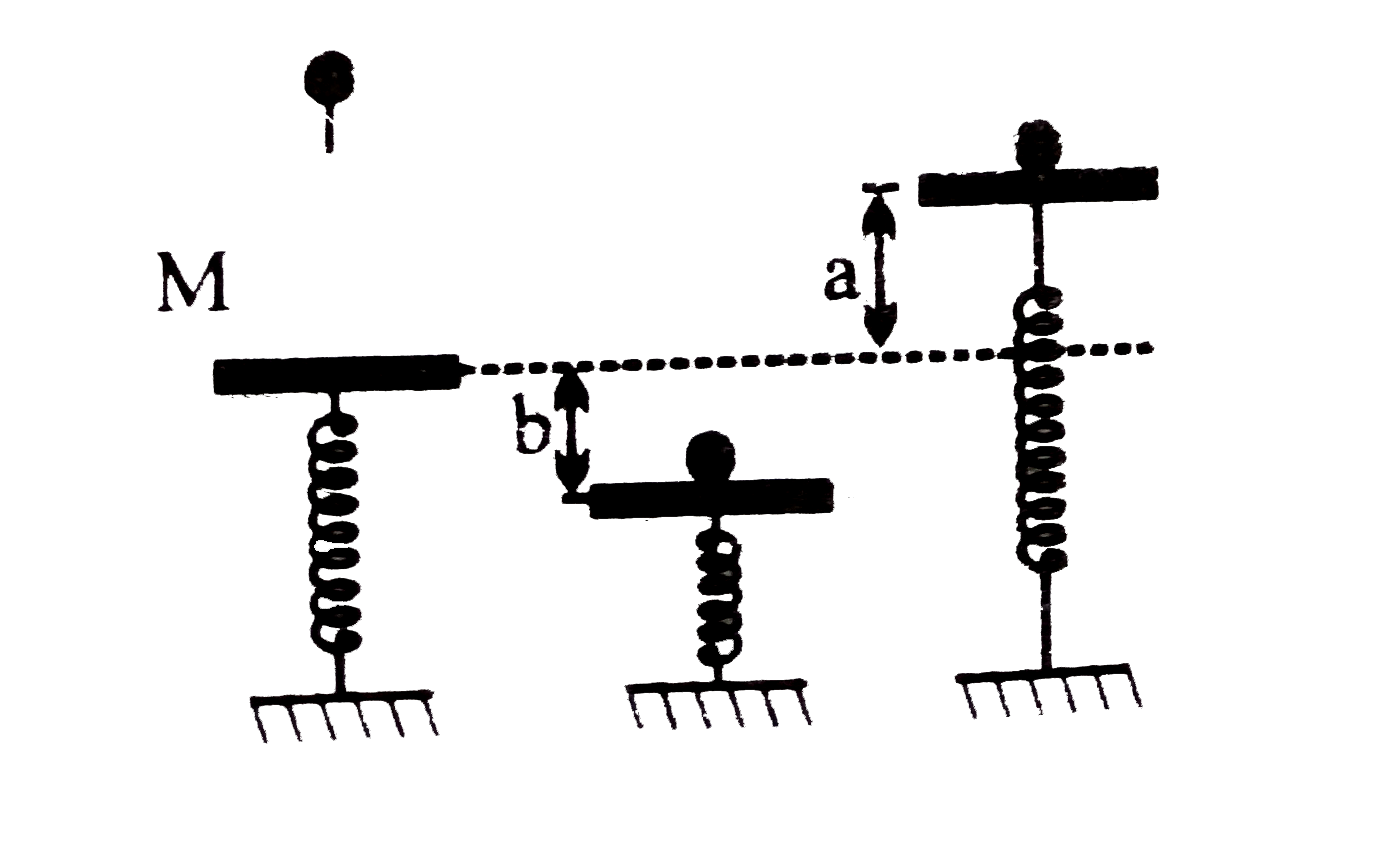
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?
The correct Answer is:A, B, C
Ans:(a)K=2mgb−a
(b)12π√kM+m
(c)(M+mb−a)abm

Amplitude =b−mgK=a+mgK( by diagram )
⇒K=2mgb−a
(b)f=1T=12π√MK+m
(c) If the ball was fropped from 'h'.
⇒Vbefore collision=√2gh
conserving momentum :
m√2gh=(m+M)V' Where V'
=ω√A2−x2=√KM+m√(b−mgK)2−(mgK)2
Squaring both sides and putting
K=2mgb−a,get h=(M+mb−a)abm.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 75
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 76
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp73
Explore 4 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
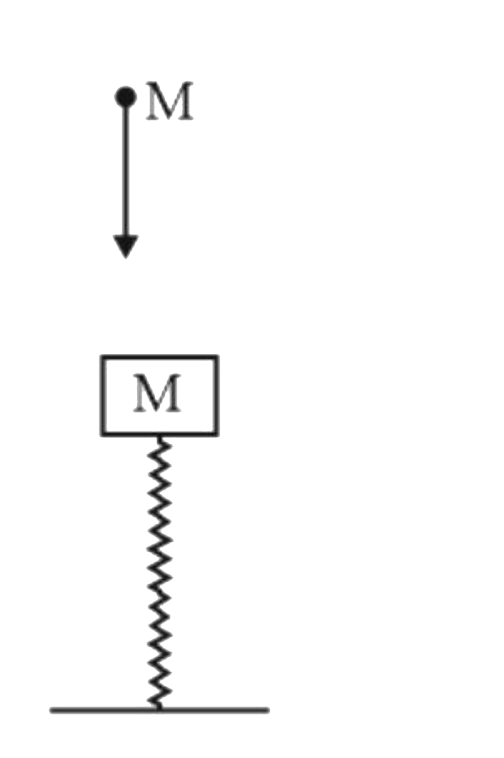
An ideal spring supports a disc of mass M. A body of mass m is released from a certain height from where it falls to hit M. The two masses stick together at the moment they touch and move together from then on . The oscillations reach to a height a above the original level of the disc and depth b blow. it The constant of the force of the spring is
View SolutionA block of mass m is dropped from height h above the ground. Find out the speed of the block when it reaches the ground.
View Solution
Knowledge Check
A ball of mass m is dropped from a heighth on a platform fixed at the top of a vertical spring, as shown in figure. The platform is depressed by a distance x. Then the spring constant is
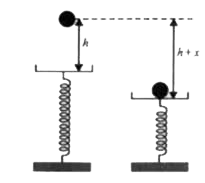 Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)
Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)A body of mass m dropped from a certain height strikes a light vertical fixed spring of stifness k. the height of its fall before touching the spring the if the maximum compression of the spring the equal to 3mgk is
A3mg2kB2mgkC3mg4kDmg4kA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk
A ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View SolutionA ball of mass 'm' drops from a height which sticks to a massless hanger after striking it. Neglecting overturning. Find out the maximum extension in rod, assuming that the rod is massless.
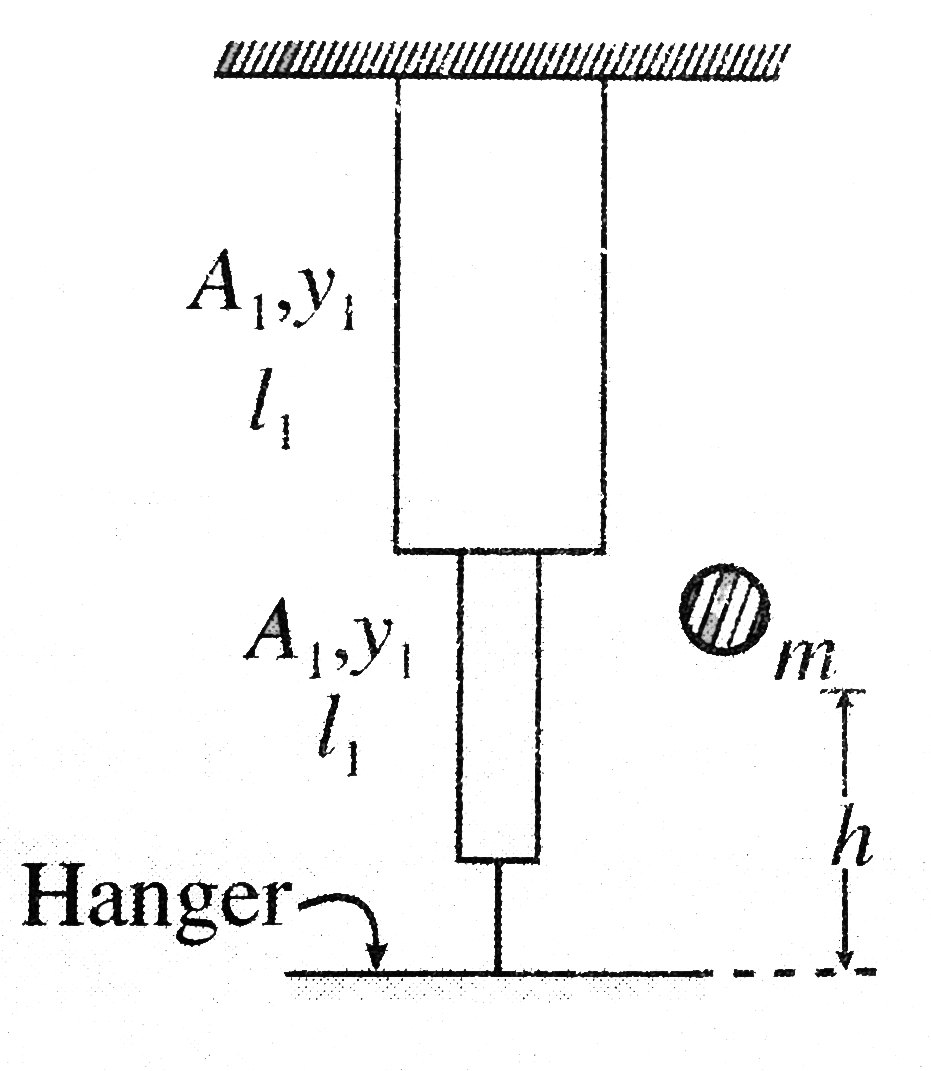
View SolutionA ball of mass 1kg is dropped from a height of 5m. (a) Find the kinetic of the ball just before it reaches the ground (b) What is the speed at this instant?
View Solution
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
View SolutionA massless platform is kept on a light elastic spring, as shown in the figure. When particle of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the particle strikes the pan, and the spring is compressed by 0.01 m. From what height should the particle be dropped to cause a compression of 0.04 m?
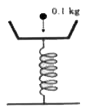
View Solution

