The resultant amplitude due to super position of $x_{1} = sin ω t, x_{2} = 5 sin (ω t + 37^{\circ})$ and $x_{3} = - 15 cos ω t$ is $:$

A

17

B

21

C

13

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$x_{1} = sin ω t, x_{2} = 5 sin (ω t + 37^{\circ})$
$x_{3} = 15 sin (ω t - π / 2)$
By the phasor diagram $,$

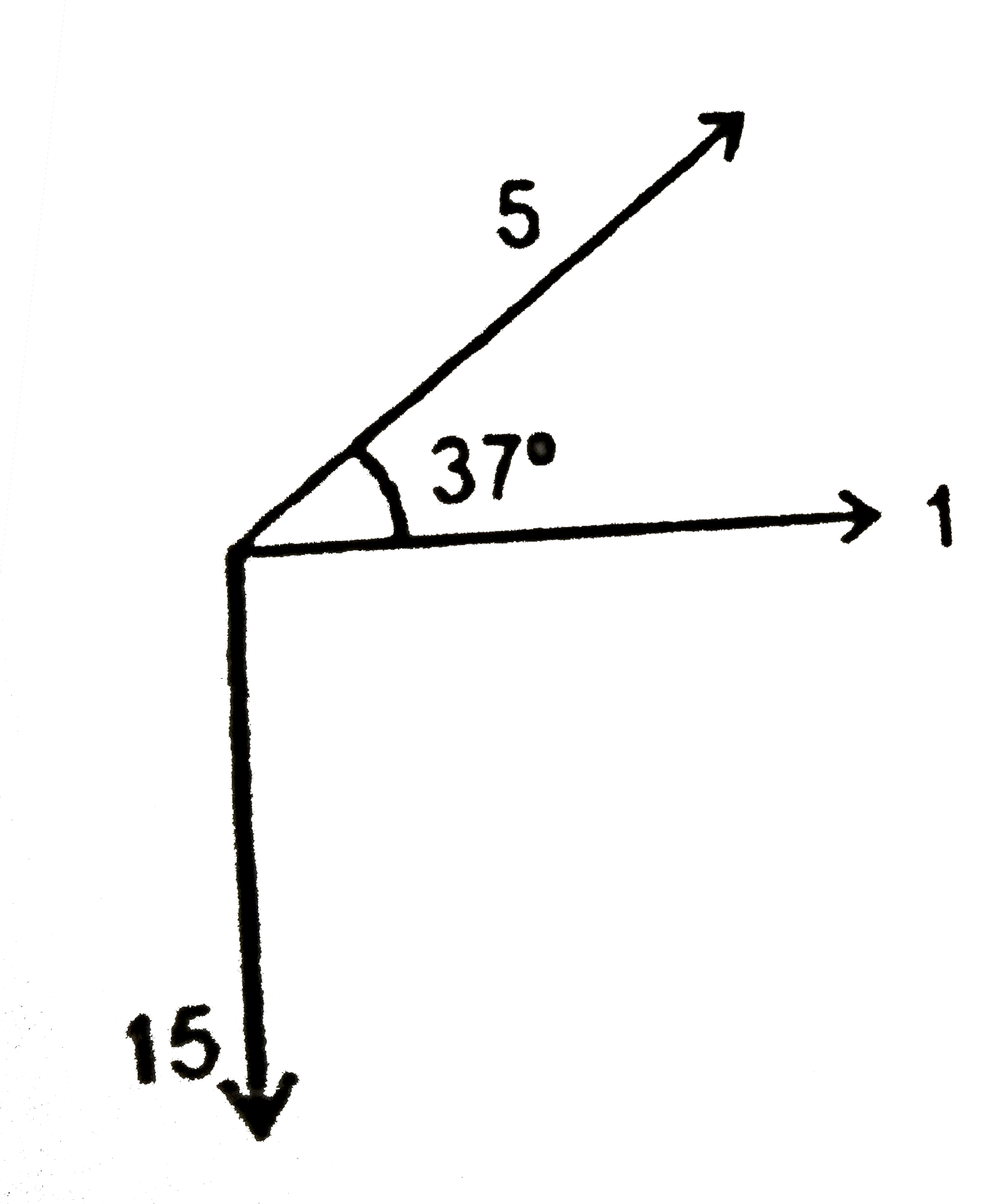
Get the resultant of these 3 vectors as 13.

Updated on:21/07/2023

|

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 77
8 Videos
DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 78
3 Videos
DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 75
5 Videos
CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos

Similar Questions

Knowledge Check

Find the resultant amplitude of the following simple harmonic equations $:$
$x_{1} = 5 sin ω t$
$x_{2} = 5 sin (ω t + 53^{\circ})$
$x_{3} = - 10 cos ω t$
A5
B10
C15
D20
The resultant amplitude due to superposition of three simple harmonic motions $x_{1} = 3 sin ω t$ ,
$x_{2} = 5 sin (ω t + 37^{\circ})$ and $x_{3} = - 15 cos ω t$ is
A $18$
B $10$
C $12$
DNone of these
Find the resultant amplitude of the following simple harmonic equations $:$
$x_{1} = 5 sin ω t$
$x_{2} = 5 sin (ω t + 53^{\circ})$
$x_{3} = - 10 cos ω t$
A5
B10
C15
D20

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 76

Home
Ask Doubt
Profile